###《Max-Margin Early Event Detectors》

Paper reading.

#@author:       gr

#@date:         2014-03-11

#@email:        forgerui@gmail.com

Early Detection Abstract:

Structured Output SVM
Processing Sequential Data
Detecing Facial Expressions, Hand Gestures, Human Acctivities

1. Introduction

1.1. potential applications

主要潜在应用：security, environmental science, healthcare, robotics.

1.2. early detection

事件早检测意味着尽可能快地检测到事件，在事件开始后结束前进行检测。如图。

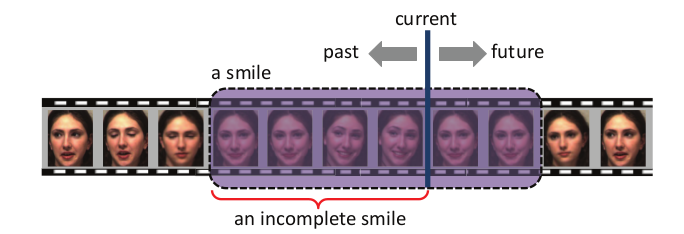
1.3. 研究现状

现在大多数的方法是离线处理的，比如：

[5] 《Actions as space-time shapes》 PAMI 2007

[9] 《Discriminative figure-centric models for joint action localization and recognition.》ICCV 2011

[10] 《The extended Cohn-Kanade dataset (CK+): A complete dataset for action unit and emotion-specified expression》 CVPR 2010

[13] 《Learning and inferring motion patterns using parametric segmental switching linear dynamic systems》 IJCV 2008

[14] 《High Five: Recognising human interactions in TV shows》 BMVC 2010

[16] 《Modeling the temporal extent of actions》 ECCV 2010

1.4. MMED

MMED基于结构输出的SVM，同时扩展成可以处理序列数据。使用部分事件作为正样例，只训练一个事件检测器去识别所有部分事件。但只是增加训练样例是不行的，我们需要这些样例满足单调性要求，即部分事件的检测得分不能高于整个事件的检测得分。MMED提供了一种方法可以去满足这个要求。

MMED的学习公式是一个受限的多项式优化问题。在3.2中，讨论两种量化损失函数的方法。我们发现，在这两种情况下，学习公式的目标就是去最小化训练数据的真实损失上界函数。

2. Previous Work

2.1. Early detection

Davis 和 Tyagi使用概率测试进行快速的人类行为识别，这是一个被动方法。它假设标准训练的生成HMM也能产生部分事件。

[2] 《Minimal-latency human action recognition using reliable-inference》 Image and Vision Computing 2006

Ryoo也使用一种被动方法进行人体行为的早检测。他使用两个词袋变量表示去解决计算问题。

[15] 《Human activity prediction: Early recognition of ongoing activities from streaming videos》 ICCV 2011

在其它领域也有一些关于早检测的研究，但都无法应用到视频事件检测上来。

2.2. Event detection

$(X^1, y^1), \cdots , (X^n, y^n)$是训练时间序列和他们相关的兴趣事件标签。$y^i = [s^i, e^i]$是时间序列$X^i$中事件开始时间和结束时间。假设事件的长度在$l_{min}$和$l_{max}$之间。$\mathcal{Y}(t)$表示从第1帧到第t帧所有时间间隔的集合。

\[\mathcal{Y}(t) = \{ y \in N^2 \mid y \subset [1, t], ~ l_{min} \le ~\mid y \mid ~ \le l_{max}\}
\]

$y=\phi$表示没有检测到事件，$y=[s, e] \in \mathcal{Y}(l)$表示从$s$帧到$e$帧的序列。$g(X)$ 表示检测器的输出结果。

\[g(X) = \arg\max_{y\in \mathcal{Y}(l) } f(X_y;\theta)
\]

传统的三种方法：

SVM 所有正例, $f(X_{y^i}^i;\theta) \ge 1$；负例小于等于1.
HMM 定义$f(\cdot, \theta)$为似然函数，通过最大似然学习参数$\theta$。
SOSVM 通过在相同时段正样例的得分大于其它段学习参数$\theta$。

3. Max-Margin Early Event Detectors

3.1. Learning with simulated sequential data

$\phi(X_y)$表示视频段$X_y$的特征向量。我们使用如下线性得分函数：

$$f(X_y;\theta) = \left\{ \begin{align*} &w^T\phi(X_y) + b & & if y \ne \emptyset, \\ & 0 & & otherwise. \end{align*} \right. $$

其中，$\theta = (w, b)$，以后使用 $f(X_y)$ 表示 $f(X_y; \theta)$。

$$~~~~~~~~g(X_{[1, t]}^i) = y_t^i~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(3)$$

$g(X_{[1,t]}^i)$ 是从开始帧到第 $t$ 帧子序列的输出结果。

\[g(X_{[1,t]}^i) = \arg\max_{y \in y(t)} f(X_y^i)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(4)
\]

得分函数期望结果如下：

\[~~~~~ f(X_{y_t^i}^i) \ge f(X_y^i) ~~ \forall y \in \mathcal{Y}(t) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (5)
\]

条件要求部分事件$y_t^i$的得分比其它任何时间$y \subset [1, t]$序列段的事件$y$得分都要高。

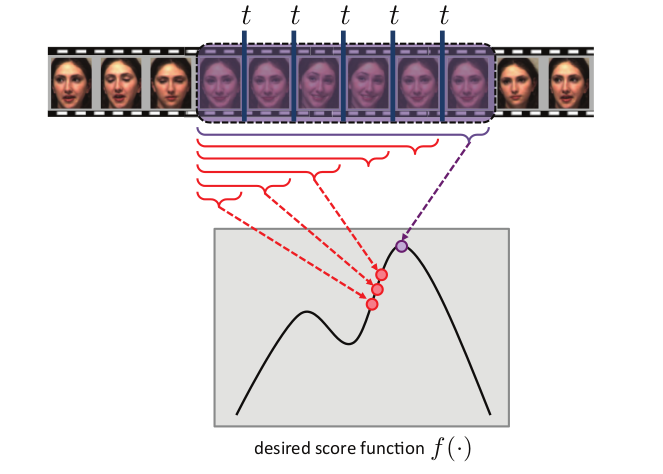
在SOSVM中，前面的条件可以通过自适应边界解决。这个边界就是$\Delta(y_t^i, y)$，它是检测器输出结果$y$和期望结果的$y_t^i$的损失函数。$\Delta (y_t^i, y) = 1 - \dfrac{2\mid y_t^i\cap y\mid}{\mid y_t^i \mid + \mid y \mid}$，条件就变成：

\[f(X_{y_t^i}^i) \ge f(X_y^i) + \Delta (y_t^i, y) ~~~~ \forall y \in \mathcal{Y}
\]

在SVM中还可以加入松驰变量，我们得到如下公式：

$$ \begin{align*}\min_{w, ~ b, ~\xi^i \ge 0} & \dfrac{1}{2}\parallel w \parallel ^2 + \dfrac{C}{n}\sum_{i = 1}^{n} \xi ^ i & (7) \\ &s.t. ~~~ f(X_{y_t^i}^i) \ge f(X_y^i) + \Delta(y_t^i, y) - \dfrac{\xi^i}{\mu(\frac{\mid y_t^i \mid}{\mid y^i \mid })} & \\ &~~~~~~~~~~~~~~~~~~~~~~\forall i, \forall t = 1, \cdots , l^i, \forall y \in \mathcal{Y}(t). & (8) \end{align*}$$

$\mu()$应该是一个递增的函数。在实验中如下配置：

$$\left\{ \begin{align*}
& \mu (x) = 0 && 0 \lt x \le \alpha \\
& \mu(x) = \dfrac{x-\alpha}{\beta - \alpha} && \alpha \lt x \le \beta \\
& \mu(x) = 1 && \beta \lt x \le 1 ~~ or ~~ x = 0
\end{align*} \right. $$

$\mu (0) = \mu(1) = 1$ 表明确定负段和正确段一样重要。

方法在线增加训练样本时，还要求检测器函数满足单调性。一个部分事件的得分不能超过包含它的事件得分。如下图：

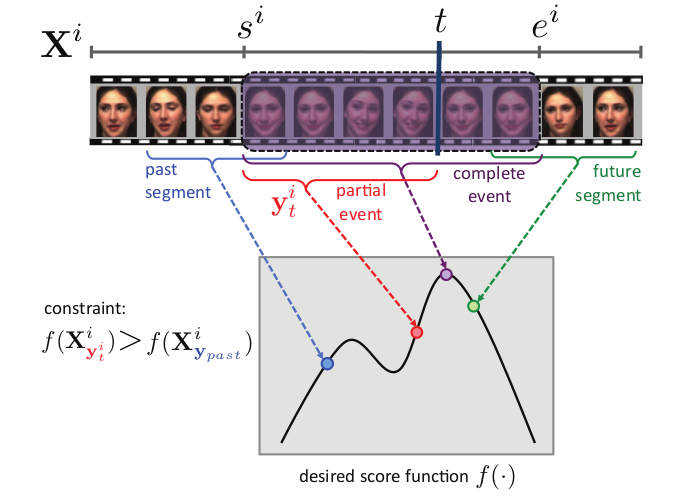
为了更好分析条件(8)，让我们分析不带松驰变量时的情况并把它划分成三种情况：

i) $t < s^i $，事件还没有开始。

ii) $t \ge s^i, y=\phi$，事件已经开始，比较部分事件和检测阈值

iii) $t \ge s^i, y \ne \phi$，事件已经开始，比较部分事件和任何非空段。

这三种情况分别是下面的条件(9)，(10)，(11):

\[f(X_y^i) \le -1 ~~~ \forall y \in \mathcal{Y}(s^i - 1) ~ \backslash ~ \{\phi\} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(9)
\]

\[f(X_{y_t^i}^i) \ge 1 ~~ \forall t \ge s^i ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(10)
\]

\[f(X_{y_t^i}^i) \ge f(X_y^i) + \Delta(y_t^i, y) ~~ \forall t \ge s^i, y \in \mathcal{Y}(t) ~ \backslash ~ \{\phi\} ~~~~~~~~~~~(11)
\]

3.2. Loss function and empirical risk minimization

由于评估需要持续进行，量化一个在线的检测器在需要不断增加评估的损失值。序列$X^i$在时间$t$的损失是$\Delta(y_t^i, y)\mu(\frac{y_t^i}{y^i})$。两种量化方式是最大值或平均值。它们产生了两个不同的经验风险。

\[R_{max}^{\Delta, \mu}(g) = \frac{1}{n} \sum_{i=1}^n max_t \{ \Delta(y_t^i, g(X_{[1,t]}^i)) \mu(\frac{\mid y_t^i \mid}{\mid y^i \mid})\}
\]

\[R_{mean}^{\Delta, \mu}(g) = \frac{1}{n} \sum_{i=1}^n mean_t \{ \Delta(y_t^i, g(X_{[1,t]}^i)) \mu(\frac{\mid y_t^i \mid}{\mid y^i \mid})\}
\]

等式(7)的学习公式将最小化上面两个经验风险的上界。

命题：$\xi ^* (g)$是等式(7)中的松驰变量，那么$\frac{1}{n}\sum_{i=1}^n \xi ^{i*}$是经验风险$R_{max}^{\Delta, \mu}(g)$，$R_{mean}^{\Delta, \mu}(g)$的上界。

证明：

4. Experiments

4.1. Evaluation criteria

ROC曲线面积： 在事件开始之前检测出来称为误检(FPR)。正确检测(TPR)是发生在感兴趣事件范围内。ROC曲线是TPR和FPR的函数。

AMOC曲线： 判别事件的检测时间长短(NTtoD)。定义NTtoD为$\dfrac{t - s + 1}{e - s + 1}$。当$t < s$时，误检时NTtoD为0。没有检测出来(t > e)时，置为$\infty$。AMOC曲线是NTtoD与FPR的函数。

F1-score 曲线： 在时间t，检测器可能输出y部件，但ground truth却是 $y^*$ 。F1-score被定义为精确率和回召率的调和均值。 $F1 := 2 \frac{Precision * Recall }{Precision + Recall}$，其中 $Precision := \dfrac{\mid y \cap y^* \mid}{\mid y \mid}$，$Recall := \dfrac{\mid y \cap y^* \mid}{\mid y^* \mid}$。

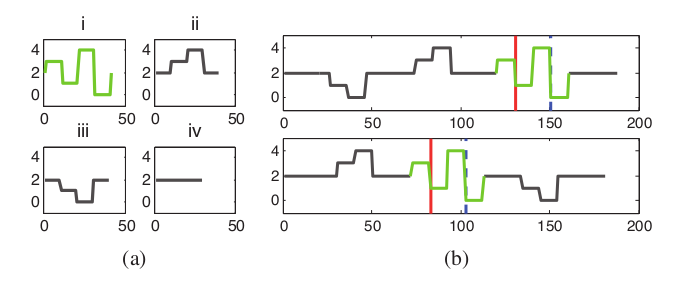
4.2. 综合数据

综合数据是组合一个兴趣事件(i)和一些其他事件序列(ii, iii, iv)。(b)图是两个例子，红色线代表我们的方法检测结果，蓝色是SOSVM结果。

4.3. Auslan dataset

当观察事件很小时，MMED的F1得分明显要好很多。

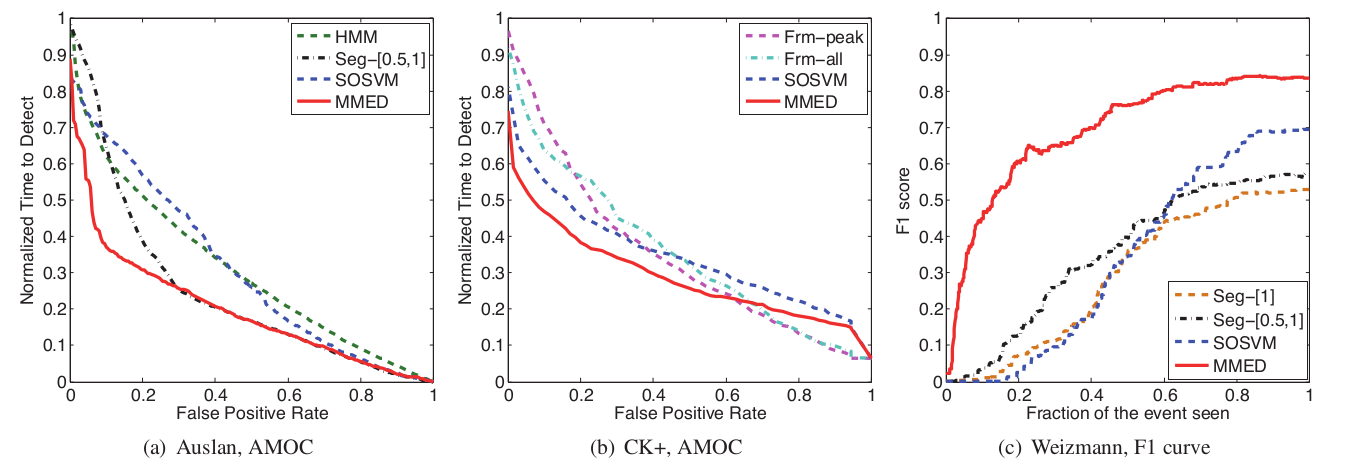
4.4. Extened Cohn-Kanade dataset

4.5. Weizmann dataset

5. Conclusion

提出MMED，可以尽可能快地检测事件。