4-2.矩阵乘法的Strassen算法详解
题目描述
请编程实现矩阵乘法，并考虑当矩阵规模较大时的优化方法。
思路分析
根据wikipedia上的介绍：两个矩阵的乘法仅当第一个矩阵B的列数和另一个矩阵A的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积AB是一个m×p矩阵，它的一个元素其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。
值得一提的是，矩阵乘法满足结合律和分配率，但并不满足交换律，如下图所示的这个例子，两个矩阵交换相乘后，结果变了：
下面咱们来具体解决这个矩阵相乘的问题。
解法一、暴力解法
其实，通过前面的分析，我们已经很明显的看出，两个具有相同维数的矩阵相乘，其复杂度为O（n^3），参考代码如下：
- //矩阵乘法，3个for循环搞定
- void Mul(int** matrixA, int** matrixB, int** matrixC)
- {
- for(int i = 0; i < 2; ++i)
- {
- for(int j = 0; j < 2; ++j)
- {
- matrixC[i][j] = 0;
- for(int k = 0; k < 2; ++k)
- {
- matrixC[i][j] += matrixA[i][k] * matrixB[k][j];
- }
- }
- }
- }
解法二、Strassen算法
在解法一中，我们用了3个for循环搞定矩阵乘法，但当两个矩阵的维度变得很大时，O（n^3）的时间复杂度将会变得很大，于是，我们需要找到一种更优的解法。
一般说来，当数据量一大时，我们往往会把大的数据分割成小的数据，各个分别处理。遵此思路，如果丢给我们一个很大的两个矩阵呢，是否可以考虑分治的方法循序渐进处理各个小矩阵的相乘，因为我们知道一个矩阵是可以分成更多小的矩阵的。
如下图，当给定一个两个二维矩阵A B时：
这两个矩阵A B相乘时，我们发现在相乘的过程中，有8次乘法运算，4次加法运算：
矩阵乘法的复杂度主要就是体现在相乘上，而多一两次的加法并不会让复杂度上升太多。故此，我们思考，是否可以让矩阵乘法的运算过程中乘法的运算次数减少，从而达到降低矩阵乘法的复杂度呢？答案是肯定的。
1969年，德国的一位数学家Strassen证明O（N^3）的解法并不是矩阵乘法的最优算法，他做了一系列工作使得最终的时间复杂度降低到了O(n^2.80)。
他是怎么做到的呢？还是用上文A B两个矩阵相乘的例子，他定义了7个变量：
如此，Strassen算法的流程如下：
- 两个矩阵A B相乘时，将A, B, C分成相等大小的方块矩阵：
；
- 可以看出C是这么得来的：
- 现在定义7个新矩阵（读者可以思考下，这7个新矩阵是如何想到的）：
- 而最后的结果矩阵C 可以通过组合上述7个新矩阵得到：
表面上看，Strassen算法仅仅比通用矩阵相乘算法好一点，因为通用矩阵相乘算法时间复杂度是
具体实现的伪代码如下：
Strassen (N,MatrixA,MatrixB,MatrixResult)
//splitting input Matrixes, into 4 submatrices each.
for i <- 0 to N/2
for j <- 0 to N/2
A11[i][j] <- MatrixA[i][j]; //a矩阵块
A12[i][j] <- MatrixA[i][j + N / 2]; //b矩阵块
A21[i][j] <- MatrixA[i + N / 2][j]; //c矩阵块
A22[i][j] <- MatrixA[i + N / 2][j + N / 2];//d矩阵块
B11[i][j] <- MatrixB[i][j]; //e 矩阵块
B12[i][j] <- MatrixB[i][j + N / 2]; //f 矩阵块
B21[i][j] <- MatrixB[i + N / 2][j]; //g 矩阵块
B22[i][j] <- MatrixB[i + N / 2][j + N / 2]; //h矩阵块
//here we calculate M1..M7 matrices .
//递归求M1
HalfSize <- N/2
AResult <- A11+A22
BResult <- B11+B22
Strassen( HalfSize, AResult, BResult, M1 ); //M1=(A11+A22)*(B11+B22) p5=(a+d)*(e+h)
//递归求M2
AResult <- A21+A22
Strassen(HalfSize, AResult, B11, M2); //M2=(A21+A22)B11 p3=(c+d)*e
//递归求M3
BResult <- B12 - B22
Strassen(HalfSize, A11, BResult, M3); //M3=A11(B12-B22) p1=a*(f-h)
//递归求M4
BResult <- B21 - B11
Strassen(HalfSize, A22, BResult, M4); //M4=A22(B21-B11) p4=d*(g-e)
//递归求M5
AResult <- A11+A12
Strassen(HalfSize, AResult, B22, M5); //M5=(A11+A12)B22 p2=(a+b)*h
//递归求M6
AResult <- A21-A11
BResult <- B11+B12
Strassen( HalfSize, AResult, BResult, M6); //M6=(A21-A11)(B11+B12) p7=(c-a)(e+f)
//递归求M7
AResult <- A12-A22
BResult <- B21+B22
Strassen(HalfSize, AResult, BResult, M7); //M7=(A12-A22)(B21+B22) p6=(b-d)*(g+h)
//计算结果子矩阵
C11 <- M1 + M4 - M5 + M7;
C12 <- M3 + M5;
C21 <- M2 + M4;
C22 <- M1 + M3 - M2 + M6;
//at this point , we have calculated the c11..c22 matrices, and now we are going to
//put them together and make a unit matrix which would describe our resulting Matrix.
for i <- 0 to N/2
for j <- 0 to N/2
MatrixResult[i][j] <- C11[i][j];
MatrixResult[i][j + N / 2] <- C12[i][j];
MatrixResult[i + N / 2][j] <- C21[i][j];
MatrixResult[i + N / 2][j + N / 2] <- C22[i][j];
具体测试代码如下：
// 4-2.矩阵乘法的Strassen算法.cpp : 定义控制台应用程序的入口点。
// #include "stdafx.h"
#include <iostream>
#include <ctime>
#include <Windows.h>
using namespace std; template<typename T>
class Strassen_class{
public:
void ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize );
void SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize );
void MUL( T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize );//朴素算法实现
void FillMatrix( T** MatrixA, T** MatrixB, int length);//A,B矩阵赋值
void PrintMatrix(T **MatrixA,int MatrixSize);//打印矩阵
void Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC);//Strassen算法实现
};
template<typename T>
void Strassen_class<T>::ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize )
{
for ( int i = 0; i < MatrixSize; i++)
{
for ( int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j];
}
}
}
template<typename T>
void Strassen_class<T>::SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize )
{
for ( int i = 0; i < MatrixSize; i++)
{
for ( int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j];
}
}
}
template<typename T>
void Strassen_class<T>::MUL( T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize )
{
for (int i=0;i<MatrixSize ;i++)
{
for (int j=0;j<MatrixSize ;j++)
{
MatrixResult[i][j]=0;
for (int k=0;k<MatrixSize ;k++)
{
MatrixResult[i][j]=MatrixResult[i][j]+MatrixA[i][k]*MatrixB[k][j];
}
}
}
} /*
c++使用二维数组，申请动态内存方法
申请
int **A;
A = new int *[desired_array_row];
for ( int i = 0; i < desired_array_row; i++)
A[i] = new int [desired_column_size]; 释放
for ( int i = 0; i < your_array_row; i++)
delete [] A[i];
delete[] A; */
template<typename T>
void Strassen_class<T>::Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC)
{ int HalfSize = N/2;
int newSize = N/2; if ( N <= 64 ) //分治门槛，小于这个值时不再进行递归计算，而是采用常规矩阵计算方法
{
MUL(MatrixA,MatrixB,MatrixC,N);
}
else
{
T** A11;
T** A12;
T** A21;
T** A22; T** B11;
T** B12;
T** B21;
T** B22; T** C11;
T** C12;
T** C21;
T** C22; T** M1;
T** M2;
T** M3;
T** M4;
T** M5;
T** M6;
T** M7;
T** AResult;
T** BResult; //making a 1 diminsional pointer based array.
A11 = new T *[newSize];
A12 = new T *[newSize];
A21 = new T *[newSize];
A22 = new T *[newSize]; B11 = new T *[newSize];
B12 = new T *[newSize];
B21 = new T *[newSize];
B22 = new T *[newSize]; C11 = new T *[newSize];
C12 = new T *[newSize];
C21 = new T *[newSize];
C22 = new T *[newSize]; M1 = new T *[newSize];
M2 = new T *[newSize];
M3 = new T *[newSize];
M4 = new T *[newSize];
M5 = new T *[newSize];
M6 = new T *[newSize];
M7 = new T *[newSize]; AResult = new T *[newSize];
BResult = new T *[newSize]; int newLength = newSize; //making that 1 diminsional pointer based array , a 2D pointer based array
for ( int i = 0; i < newSize; i++)
{
A11[i] = new T[newLength];
A12[i] = new T[newLength];
A21[i] = new T[newLength];
A22[i] = new T[newLength]; B11[i] = new T[newLength];
B12[i] = new T[newLength];
B21[i] = new T[newLength];
B22[i] = new T[newLength]; C11[i] = new T[newLength];
C12[i] = new T[newLength];
C21[i] = new T[newLength];
C22[i] = new T[newLength]; M1[i] = new T[newLength];
M2[i] = new T[newLength];
M3[i] = new T[newLength];
M4[i] = new T[newLength];
M5[i] = new T[newLength];
M6[i] = new T[newLength];
M7[i] = new T[newLength]; AResult[i] = new T[newLength];
BResult[i] = new T[newLength]; }
//splitting input Matrixes, into 4 submatrices each.
for (int i = 0; i < N / 2; i++)
{
for (int j = 0; j < N / 2; j++)
{
A11[i][j] = MatrixA[i][j];
A12[i][j] = MatrixA[i][j + N / 2];
A21[i][j] = MatrixA[i + N / 2][j];
A22[i][j] = MatrixA[i + N / 2][j + N / 2]; B11[i][j] = MatrixB[i][j];
B12[i][j] = MatrixB[i][j + N / 2];
B21[i][j] = MatrixB[i + N / 2][j];
B22[i][j] = MatrixB[i + N / 2][j + N / 2]; }
} //here we calculate M1..M7 matrices .
//M1[][]
ADD( A11,A22,AResult, HalfSize);
ADD( B11,B22,BResult, HalfSize); //p5=(a+d)*(e+h)
Strassen( HalfSize, AResult, BResult, M1 ); //now that we need to multiply this , we use the strassen itself . //M2[][]
ADD( A21,A22,AResult, HalfSize); //M2=(A21+A22)B11 p3=(c+d)*e
Strassen(HalfSize, AResult, B11, M2); //Mul(AResult,B11,M2); //M3[][]
SUB( B12,B22,BResult, HalfSize); //M3=A11(B12-B22) p1=a*(f-h)
Strassen(HalfSize, A11, BResult, M3); //Mul(A11,BResult,M3); //M4[][]
SUB( B21, B11, BResult, HalfSize); //M4=A22(B21-B11) p4=d*(g-e)
Strassen(HalfSize, A22, BResult, M4); //Mul(A22,BResult,M4); //M5[][]
ADD( A11, A12, AResult, HalfSize); //M5=(A11+A12)B22 p2=(a+b)*h
Strassen(HalfSize, AResult, B22, M5); //Mul(AResult,B22,M5); //M6[][]
SUB( A21, A11, AResult, HalfSize);
ADD( B11, B12, BResult, HalfSize); //M6=(A21-A11)(B11+B12) p7=(c-a)(e+f)
Strassen( HalfSize, AResult, BResult, M6); //Mul(AResult,BResult,M6); //M7[][]
SUB(A12, A22, AResult, HalfSize);
ADD(B21, B22, BResult, HalfSize); //M7=(A12-A22)(B21+B22) p6=(b-d)*(g+h)
Strassen(HalfSize, AResult, BResult, M7); //Mul(AResult,BResult,M7); //C11 = M1 + M4 - M5 + M7;
ADD( M1, M4, AResult, HalfSize);
SUB( M7, M5, BResult, HalfSize);
ADD( AResult, BResult, C11, HalfSize); //C12 = M3 + M5;
ADD( M3, M5, C12, HalfSize); //C21 = M2 + M4;
ADD( M2, M4, C21, HalfSize); //C22 = M1 + M3 - M2 + M6;
ADD( M1, M3, AResult, HalfSize);
SUB( M6, M2, BResult, HalfSize);
ADD( AResult, BResult, C22, HalfSize); //at this point , we have calculated the c11..c22 matrices, and now we are going to
//put them together and make a unit matrix which would describe our resulting Matrix.
//组合小矩阵到一个大矩阵
for (int i = 0; i < N/2 ; i++)
{
for (int j = 0 ; j < N/2 ; j++)
{
MatrixC[i][j] = C11[i][j];
MatrixC[i][j + N / 2] = C12[i][j];
MatrixC[i + N / 2][j] = C21[i][j];
MatrixC[i + N / 2][j + N / 2] = C22[i][j];
}
} // 释放矩阵内存空间
for (int i = 0; i < newLength; i++)
{
delete[] A11[i];delete[] A12[i];delete[] A21[i];
delete[] A22[i]; delete[] B11[i];delete[] B12[i];delete[] B21[i];
delete[] B22[i];
delete[] C11[i];delete[] C12[i];delete[] C21[i];
delete[] C22[i];
delete[] M1[i];delete[] M2[i];delete[] M3[i];delete[] M4[i];
delete[] M5[i];delete[] M6[i];delete[] M7[i];
delete[] AResult[i];delete[] BResult[i] ;
}
delete[] A11;delete[] A12;delete[] A21;delete[] A22;
delete[] B11;delete[] B12;delete[] B21;delete[] B22;
delete[] C11;delete[] C12;delete[] C21;delete[] C22;
delete[] M1;delete[] M2;delete[] M3;delete[] M4;delete[] M5;
delete[] M6;delete[] M7;
delete[] AResult;
delete[] BResult ; }//end of else } template<typename T>
void Strassen_class<T>::FillMatrix( T** MatrixA, T** MatrixB, int length)
{
for(int row = 0; row<length; row++)
{
for(int column = 0; column<length; column++)
{ MatrixB[row][column] = (MatrixA[row][column] = rand() %5);
//matrix2[row][column] = rand() % 2;//ba hazfe in khat 50% afzayeshe soorat khahim dasht
} }
}
template<typename T>
void Strassen_class<T>::PrintMatrix(T **MatrixA,int MatrixSize)
{
cout<<endl;
for(int row = 0; row<MatrixSize; row++)
{
for(int column = 0; column<MatrixSize; column++)
{ cout<<MatrixA[row][column]<<"\t";
if ((column+1)%((MatrixSize)) == 0)
cout<<endl;
} }
cout<<endl;
} int _tmain(int argc, _TCHAR* argv[])
{
Strassen_class<int> stra;//定义Strassen_class类对象
int MatrixSize = 0; int** MatrixA; //存放矩阵A
int** MatrixB; //存放矩阵B
int** MatrixC; //存放结果矩阵 clock_t startTime_For_Normal_Multipilication ;
clock_t endTime_For_Normal_Multipilication ; clock_t startTime_For_Strassen ;
clock_t endTime_For_Strassen ;
srand(time(0)); cout<<"\n请输入矩阵大小(必须是2的幂指数值(例如:32,64,512,..): ";
cin>>MatrixSize; int N = MatrixSize;//for readiblity. //申请内存
MatrixA = new int *[MatrixSize];
MatrixB = new int *[MatrixSize];
MatrixC = new int *[MatrixSize]; for (int i = 0; i < MatrixSize; i++)
{
MatrixA[i] = new int [MatrixSize];
MatrixB[i] = new int [MatrixSize];
MatrixC[i] = new int [MatrixSize];
} stra.FillMatrix(MatrixA,MatrixB,MatrixSize); //矩阵赋值 //*******************conventional multiplication test
cout<<"朴素矩阵算法开始时钟: "<< (startTime_For_Normal_Multipilication = clock()); stra.MUL(MatrixA,MatrixB,MatrixC,MatrixSize);//朴素矩阵相乘算法 T(n) = O(n^3) cout<<"\n朴素矩阵算法结束时钟: "<< (endTime_For_Normal_Multipilication = clock()); cout<<"\n矩阵运算结果... \n";
stra.PrintMatrix(MatrixC,MatrixSize); //*******************Strassen multiplication test
cout<<"\nStrassen算法开始时钟: "<< (startTime_For_Strassen = clock()); stra.Strassen( N, MatrixA, MatrixB, MatrixC ); //strassen矩阵相乘算法 cout<<"\nStrassen算法结束时钟: "<<(endTime_For_Strassen = clock()); cout<<"\n矩阵运算结果... \n";
stra.PrintMatrix(MatrixC,MatrixSize); cout<<"矩阵大小 "<<MatrixSize;
cout<<"\n朴素矩阵算法: "<<(endTime_For_Normal_Multipilication - startTime_For_Normal_Multipilication)<<" Clocks.."<<(endTime_For_Normal_Multipilication - startTime_For_Normal_Multipilication)/CLOCKS_PER_SEC<<" Sec";
cout<<"\nStrassen算法:"<<(endTime_For_Strassen - startTime_For_Strassen)<<" Clocks.."<<(endTime_For_Strassen - startTime_For_Strassen)/CLOCKS_PER_SEC<<" Sec\n";
system("Pause"); return 0;
}
运行结果：
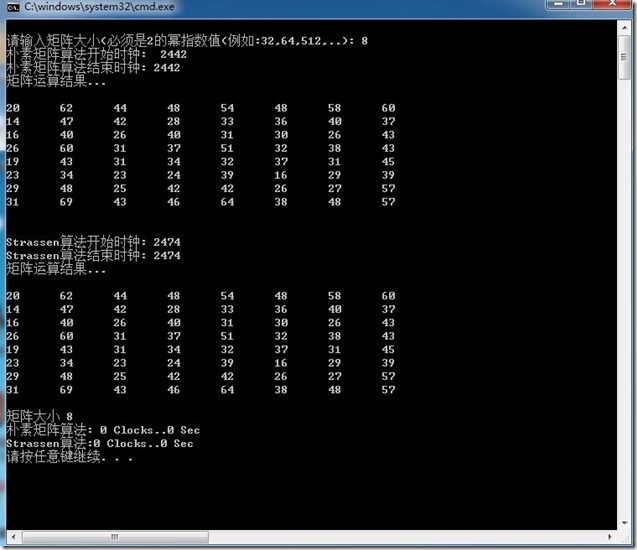
性能分析：
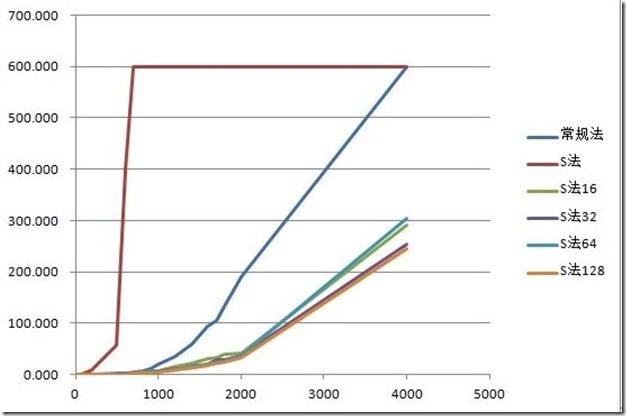
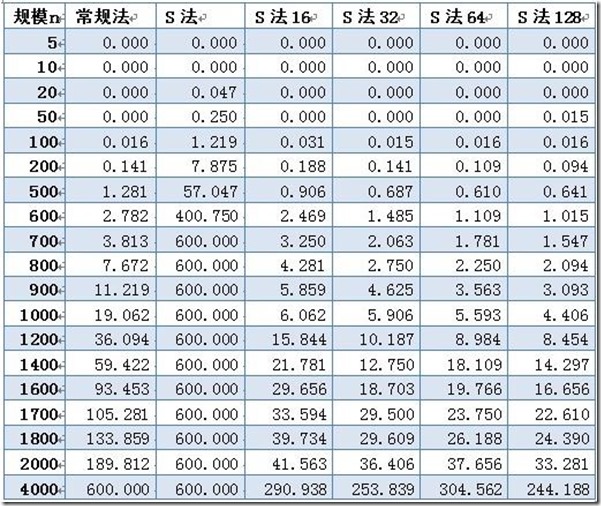
数据取600位上界，即超过10分钟跳出。可以看到使用Strassen算法时，耗时不但没有减少，反而剧烈增多，在n=700时计算时间就无法忍受。仔细研究后发现，采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势。于是对Strassen算法做出改进，设定一个界限。当n<界限时，使用普通法计算矩阵，而不继续分治递归。
改进后算法优势明显，就算时间大幅下降。之后，针对不同大小的界限进行试验。在初步试验中发现，当数据规模小于1000时，下界S法的差别不大，规模大于1000以后，n取值越大，消耗时间下降。最优的界限值在32～128之间。
因为计算机每次运算时的系统环境不同（CPU占用、内存占用等），所以计算出的时间会有一定浮动。虽然这样，试验结果已经能得出结论Strassen算法比常规法优势明显。使用下界法改进后，在分治效率和动态分配内存间取舍，针对不同的数据规模稍加试验可以得到一个最优的界限。
小结：
1）采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势
2）于是对Strassen算法做出改进，设定一个界限。当n<界限时，使用普通法计算矩阵，而不继续分治递归。需要合理设置界限，不同环境（硬件配置）下界限不同
3）矩阵乘法一般意义上还是选择的是朴素的方法，只有当矩阵变稠密，而且矩阵的阶数很大时，才会考虑使用Strassen算法。
4-2.矩阵乘法的Strassen算法详解的更多相关文章
- 《算法导论》——矩阵乘法的Strassen算法
前言: 很多朋友看到我写的<算法导论>系列,可能会觉得云里雾里,不知所云.这里我再次说明,本系列博文时配合<算法导论>一书,给出该书涉及的算法的c++实现.请结合<算法导 ...
- 第四章 分治策略 4.2 矩阵乘法的Strassen算法
package chap04_Divide_And_Conquer; import static org.junit.Assert.*; import java.util.Arrays; import ...
- 机器学习经典算法详解及Python实现--基于SMO的SVM分类器
原文:http://blog.csdn.net/suipingsp/article/details/41645779 支持向量机基本上是最好的有监督学习算法,因其英文名为support vector ...
- EM算法详解
EM算法详解 1 极大似然估计 假设有如图1的X所示的抽取的n个学生某门课程的成绩,又知学生的成绩符合高斯分布f(x|μ,σ2),求学生的成绩最符合哪种高斯分布,即μ和σ2最优值是什么? 图1 学生成 ...
- 【最短路径Floyd算法详解推导过程】看完这篇，你还能不懂Floyd算法？还不会？
简介 Floyd-Warshall算法(Floyd-Warshall algorithm),是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似.该算法名称以 ...
- 第二十九节，目标检测算法之R-CNN算法详解
Girshick, Ross, et al. “Rich feature hierarchies for accurate object detection and semantic segmenta ...
- FloodFill算法详解及应用
啥是 FloodFill 算法呢,最直接的一个应用就是「颜色填充」,就是 Windows 绘画本中那个小油漆桶的标志,可以把一块被圈起来的区域全部染色. 这种算法思想还在许多其他地方有应用.比如说扫雷 ...
- BM算法 Boyer-Moore高质量实现代码详解与算法详解
Boyer-Moore高质量实现代码详解与算法详解 鉴于我见到对算法本身分析非常透彻的文章以及实现的非常精巧的文章,所以就转载了,本文的贡献在于将两者结合起来,方便大家了解代码实现! 算法详解转自:h ...
- kmp算法详解
转自:http://blog.csdn.net/ddupd/article/details/19899263 KMP算法详解 KMP算法简介: KMP算法是一种高效的字符串匹配算法,关于字符串匹配最简 ...
随机推荐
- 解决eclipse配置Tomcat时找不到server选项
集成Eclipse和Tomcat时找不到server选项: 按照网上的步骤如下: 在Eclipse中,窗口(window)——首选项(preferences)——服务器(Server)——运行时环境( ...
- 插件介绍 ：cropper是一款使用简单且功能强大的图片剪裁jQuery插件。
简要教程 cropper是一款使用简单且功能强大的图片剪裁jQuery插件.该图片剪裁插件支持图片放大缩小,支持鼠标滚轮操作,支持图片旋转,支持触摸屏设备,支持canvas,并且支持跨浏览器使用. c ...
- CSAPP2e:Shell lab 解答
期中之后的第一个lab 就是实现一个简单的Shell 程序,程序的大部分已经写好,只需要实现 eval 函数和处理信号的sigchld_handle, sigint_handle, sigtstp_h ...
- AIX学习笔记（更新中）
AIX操作系统基本命令 系统的进入和退出login: 输入用户名(例如:user01)password: 输入用户口令若用户名及口令均正确,则用户将登陆成功.此时系统会出现命令提示符 $或#,即表示可 ...
- CSS图片翻转例子
dfdfdfdfdf <!DOCTYPE html> <html> <head> <meta charset=" ...
- 20141017--循环语句for 穷举
穷举:把所有的可能性都列举一遍 1.羽毛球怕15元一个,球3元一个,水2元一瓶,一共有200元,每种至少一个,列出所有可能: 2. 50元钱,有面值2元,3元,5元,不要求每种至少一张,有多少种组 ...
- UI1_UITableViewSearchController
// UI1_UITableViewSearchController // // Created by zhangxueming on 15/7/15. // Copyright (c) 2015年 ...
- Ant打jar包指定MainClass
一般用ant打jar的时候不用指定程序的入口!这个jar一般是给其他app引用的. 但是如果该jar就是程序的启动jar.例如: java -jar abc.jar 这个时候需要指定jar的入口类! ...
- c++学习——类成员的访问权限
成员的访问权限 Public: 任何人,尤其是那些要使用这个类库的客户程序员,都能访问那个紧跟在public 后面声明的成员. 默认的package: 在同一个目录里面的文件,并且都没有明确指明它是属 ...
- [sql server] 如何阻止SELECT * 语句
我们每个人都知道是个不好的做法,但有时我们还是要这样做:我们执行SELECT * 语句.这个方法有很多弊端: 你从你的表里返回每个列,甚至后期加的列.想下如果你的查询里将来加上了VARCHAR(MAX ...