Skip list--reference wiki

In computer science, a skip list is a data structure that allows fast search within an ordered sequence of elements. Fast search is made possible by maintaining a linked hierarchy of subsequences, each skipping over fewer elements. Searching starts in the sparsest subsequence until two consecutive elements have been found, one smaller and one larger than the element searched for. Via the linked hierarchy these two elements link to elements of the next sparsest subsequence where searching is continued until finally we are searching in the full sequence. The elements that are skipped over may be chosen probabilistically.^[2][3]

 

Properties：

  Consists of several levels.

  All keys appear in level 1

  Each level is a sorted list.

  If key x appears in level i, then it also appears in all levels below i

  An element in level i points (via down pointer) to the element with the same key in the level below.

  In each level the keys -1 and 1 appear. (In our implementation, INT_MIN and INT_MAX

  Top points to the smallest element in the highest level.

 

cost：

  The expected number of levels is O( log n )    

   (here n  is the numer of elements)

  The expected time for insert/delete/find is O( log n )

  The expected size (number of cells) is O(n )

 

Skip List
Type	List
Invented	1989
Invented by	W. Pugh
Time complexity in big O notation
	Average	Worst case
Space	O(n)	O(n log n)[1]
Search	O(log n)	O(n)[1]
Insert	O(log n)	O(n)
Delete	O(log n)	O(n)

Contents

• 1 Description
  • 1.1 Implementation details
  • 1.2 Indexable skiplist
• 2 History
• 3 Usages
• 4 See also
• 5 References
• 6 External links

Description

A skip list is built in layers. The bottom layer is an ordinary ordered linked list. Each higher layer acts as an "express lane" for the lists below, where an element in layer i appears in layer i+1 with some fixed probability p (two commonly used values for p are 1/2 or 1/4). On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) in 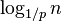 lists.

A search for a target element begins at the head element in the top list, and proceeds horizontally until the current element is greater than or equal to the target. If the current element is equal to the target, it has been found. If the current element is greater than the target, or the search reaches the end of the linked list, the procedure is repeated after returning to the previous element and dropping down vertically to the next lower list. The expected number of steps in each linked list is at most 1/p, which can be seen by tracing the search path backwards from the target until reaching an element that appears in the next higher list or reaching the beginning of the current list. Therefore, the total expected cost of a search is  which is 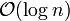 when p is a constant. By choosing different values of p, it is possible to trade search costs against storage costs.

Implementation details

Inserting elements to skip list

The elements used for a skip list can contain more than one pointer since they can participate in more than one list.

Insertions and deletions are implemented much like the corresponding linked-list operations, except that "tall" elements must be inserted into or deleted from more than one linked list.

 operations, which force us to visit every node in ascending order (such as printing the entire list), provide the opportunity to perform a behind-the-scenes derandomization of the level structure of the skip-list in an optimal way, bringing the skip list to 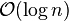 search time. (Choose the level of the i'th finite node to be 1 plus the number of times we can repeatedly divide i by 2 before it becomes odd. Also, i=0 for the negative infinity header as we have the usual special case of choosing the highest possible level for negative and/or positive infinite nodes.) However this also allows someone to know where all of the higher-than-level 1 nodes are and delete them.

Alternatively, we could make the level structure quasi-random in the following way:

make all nodes level 1
j ← 1
while the number of nodes at level j > 1 do
  for each i'th node at level j do
    if i is odd
      if i is not the last node at level j
        randomly choose whether to promote it to level j+1
      else
        do not promote
      end if
    else if i is even and node i-1 was not promoted
      promote it to level j+1
    end if
  repeat
  j ← j + 1
repeat

Like the derandomized version, quasi-randomization is only done when there is some other reason to be running a  operation (which visits every node).

The advantage of this quasi-randomness is that it doesn't give away nearly as much level-structure related information to an adversarial user as the de-randomized one. This is desirable because an adversarial user who is able to tell which nodes are not at the lowest level can pessimize performance by simply deleting higher-level nodes. The search performance is still guaranteed to be logarithmic.

It would be tempting to make the following "optimization": In the part which says "Next, for each i'th...", forget about doing a coin-flip for each even-odd pair. Just flip a coin once to decide whether to promote only the even ones or only the odd ones. Instead of 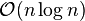 coin flips, there would only be  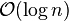of them. Unfortunately, this gives the adversarial user a 50/50 chance of being correct upon guessing that all of the even numbered nodes (among the ones at level 1 or higher) are higher than level one. This is despite the property that he has a very low probability of guessing that a particular node is at level N for some integer N.

A skip list does not provide the same absolute worst-case performance guarantees as more traditional balanced tree data structures, because it is always possible (though with very low probability) that the coin-flips used to build the skip list will produce a badly balanced structure. However, they work well in practice, and the randomized balancing scheme has been argued to be easier to implement than the deterministic balancing schemes used in balanced binary search trees. Skip lists are also useful in parallel computing, where insertions can be done in different parts of the skip list in parallel without any global rebalancing of the data structure. Such parallelism can be especially advantageous for resource discovery in an ad-hoc Wireless network because a randomized skip list can be made robust to the loss of any single node.^[4]

There has been some evidence that skip lists have worse real-world performance and space requirements than B trees due to memory locality and other issues.^[5]

Indexable skiplist

As described above, a skiplist is capable of fast 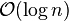 insertion and removal of values from a sorted sequence, but it has only slow  lookups of values at a given position in the sequence (i.e. return the 500th value); however, with a minor modification the speed of random access indexed lookups can be improved to .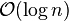

For every link, also store the width of the link. The width is defined as the number of bottom layer links being traversed by each of the higher layer "express lane" links.

For example, here are the widths of the links in the example at the top of the page:

   1                               10
 o---> o---------------------------------------------------------> o    Top level
   1           3              2                    5
 o---> o---------------> o---------> o---------------------------> o    Level 3
   1        2        1        2                    5
 o---> o---------> o---> o---------> o---------------------------> o    Level 2
   1     1     1     1     1     1     1     1     1     1     1
 o---> o---> o---> o---> o---> o---> o---> o---> o---> o---> o---> o    Bottom level

Head  1st   2nd   3rd   4th   5th   6th   7th   8th   9th   10th  NIL
      Node  Node  Node  Node  Node  Node  Node  Node  Node  Node

Notice that the width of a higher level link is the sum of the component links below it (i.e. the width 10 link spans the links of widths 3, 2 and 5 immediately below it). Consequently, the sum of all widths is the same on every level (10 + 1 = 1 + 3 + 2 + 5 = 1 + 2 + 1 + 2 + 5).

To index the skiplist and find the i'th value, traverse the skiplist while counting down the widths of each traversed link. Descend a level whenever the upcoming width would be too large.

For example, to find the node in the fifth position (Node 5), traverse a link of width 1 at the top level. Now four more steps are needed but the next width on this level is ten which is too large, so drop one level. Traverse one link of width 3. Since another step of width 2 would be too far, drop down to the bottom level. Now traverse the final link of width 1 to reach the target running total of 5 (1+3+1).

 function lookupByPositionIndex(i)
     node ← head
     i ← i + 1                           # don't count the head as a step
     for level from top to bottom do
          while i ≥ node.width[level] do # if next step is not too far
              i ← i - node.width[level]  # subtract the current width
              node ← node.next[level]    # traverse forward at the current level
          repeat
     repeat
     return node.value
 end function

This method of implementing indexing is detailed in Section 3.4 Linear List Operations in "A skip list cookbook" by William Pugh.

History

Skip lists were first described in 1990 by William Pugh.^[2]

To quote the author:

Skip lists are a probabilistic data structure that seem likely to supplant balanced trees as the implementation method of choice for many applications. Skip list algorithms have the same asymptotic expected time bounds as balanced trees and are simpler, faster and use less space.

Usages

List of applications and frameworks that use skip lists:

• Cyrus IMAP server offers a "skiplist" backend DB implementation (source file)
• Lucene uses skip lists to search delta-encoded posting lists in logarithmic time.
• QMap (up to Qt 4) template class of Qt that provides a dictionary.
• Redis, an ANSI-C open-source persistent key/value store for Posix systems, uses skip lists in its implementation of ordered sets.^[6]
• nessDB, a very fast key-value embedded Database Storage Engine (Using log-structured-merge (LSM) trees), uses skip lists for its memtable.
• skipdb is an open-source database format using ordered key/value pairs.
• ConcurrentSkipListSet and ConcurrentSkipListMap in the Java 1.6 API.
• leveldb, a fast key-value storage library written at Google that provides an ordered mapping from string keys to string values
• Skip lists are used for efficient statistical computations of running medians (also known as moving medians).

Skip lists are also used in distributed applications (where the nodes represent physical computers, and pointers represent network connections) and for implementing highly scalable concurrent priority queues with less lock contention,^[7] or even without locking,^[8][9][10] as well lockless concurrent dictionaries.^[11] There are also several US patents for using skip lists to implement (lockless) priority queues and concurrent dictionaries.^{[citation needed]}

See also

• Bloom filter
• Skip graph
• Skip trees, an alternative data structure to Skip lists in a concurrent approach: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.47.514
• Skip tree graphs: http://www0.cs.ucl.ac.uk/staff/a.gonzalezbeltran/pubs/icc2007.pdf, http://www0.cs.ucl.ac.uk/staff/a.gonzalezbeltran/pubs/AGB-comcom08.pdf

References

1. ^ Jump up to:^a b http://www.cs.uwaterloo.ca/research/tr/1993/28/root2side.pdf
2. ^ Jump up to:^a b Pugh, W. (1990). "Skip lists: A probabilistic alternative to balanced trees". Communications of the ACM 33 (6): 668. doi:10.1145/78973.78977. edit
3. Jump up^ Deterministic skip lists
4. Jump up^ Shah, Gauri Ph.D.; James Aspnes (December 2003). Distributed Data Structures for Peer-to-Peer Systems (PDF). Retrieved 2008-09-23.
5. Jump up^ http://resnet.uoregon.edu/~gurney_j/jmpc/skiplist.html
6. Jump up^ "Redis ordered set implementation".
7. Jump up^ Shavit, N.; Lotan, I. (2000). "Skiplist-based concurrent priority queues". Proceedings 14th International Parallel and Distributed Processing Symposium. IPDPS 2000. p. 263.doi:10.1109/IPDPS.2000.845994. ISBN 0-7695-0574-0. edit
8. Jump up^ Sundell, H.; Tsigas, P. (2003). "Fast and lock-free concurrent priority queues for multi-thread systems". Proceedings International Parallel and Distributed Processing Symposium. p. 11. doi:10.1109/IPDPS.2003.1213189. ISBN 0-7695-1926-1. edit
9. Jump up^ Fomitchev, M.; Ruppert, E. (2004). "Lock-free linked lists and skip lists". Proceedings of the twenty-third annual ACM symposium on Principles of distributed computing - PODC '04. p. 50. doi:10.1145/1011767.1011776. ISBN 1581138024. edit
10. Jump up^ Bajpai, R.; Dhara, K. K.; Krishnaswamy, V. (2008). "QPID: A Distributed Priority Queue with Item Locality". 2008 IEEE International Symposium on Parallel and Distributed Processing with Applications. p. 215. doi:10.1109/ISPA.2008.90. ISBN 978-0-7695-3471-8. edit
11. Jump up^ Sundell, H. K.; Tsigas, P. (2004). "Scalable and lock-free concurrent dictionaries". Proceedings of the 2004 ACM symposium on Applied computing - SAC '04. p. 1438.doi:10.1145/967900.968188. ISBN 1581138121. edit

External links

• "Skip list" entry in the Dictionary of Algorithms and Data Structures
• Skip Lists: A Linked List with Self-Balancing BST-Like Properties on MSDN in C# 2.0
• SkipDB, a BerkeleyDB-style database implemented using skip lists.
• Skip Lists lecture (MIT OpenCourseWare: Introduction to Algorithms)
• Open Data Structures - Chapter 4 - Skiplists

Demo applets

• Skip List Applet by Kubo Kovac
• Thomas Wenger's demo applet on skiplists

Implementations

• A generic Skip List in C++ by Antonio Gulli
• Algorithm::SkipList, implementation in Perl on CPAN
• John Shipman's implementation in Python
• Raymond Hettinger's implementation in Python
• A Lua port of John Shipman's Python version
• Java Implementation with index based access
• ConcurrentSkipListSet documentation for Java 6 (and sourcecode)