ansj构造最短路径
一、前言
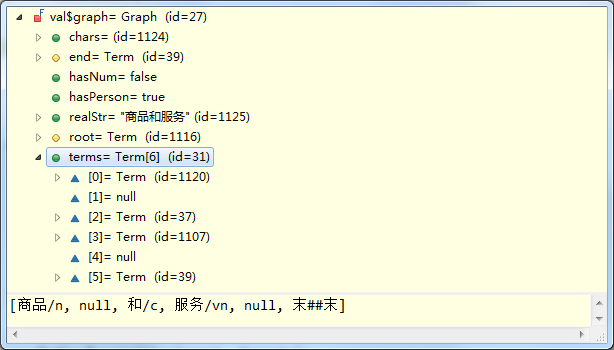
String str = "商品和服务" ;
Result result = ToAnalysis.parse(str);
System.out.println(result.getTerms());
graph.walkPath();
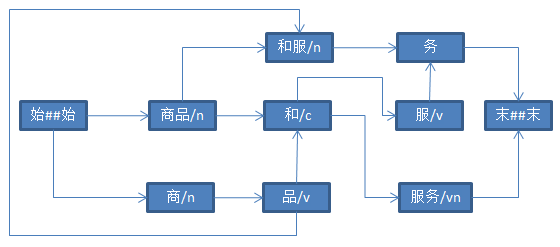

char c = chars[to];
TermNatures tn = DATDictionary.getItem(c).termNatures;
if (tn == null || tn == TermNatures.NULL) {
tn = TermNatures.NULL;
}
terms[to] = new Term(String.valueOf(c), to, tn);
二、理论基础
double value = -Math.log(dSmoothingPara * frequency / (MAX_FREQUENCE + 80000) + (1 - dSmoothingPara) * ((1 - dTemp) * nTwoWordsFreq / frequency + dTemp));
\begin{aligned}
- \log P(w_{i} | w_{i-1}) & \approx - \log \left[ aP(w_{i-1}) + (1-a) P(w_{i}|w_{i-1}) \right] \\
& \approx - \log \left[ a\frac{f(w_i)}{N} + (1-a) \left( \frac{(1-\lambda)f(w_{i-1},w_i)}{f(w_{i-1})} + \lambda \right) \right]
\end{aligned}
三、具体打分流程如下
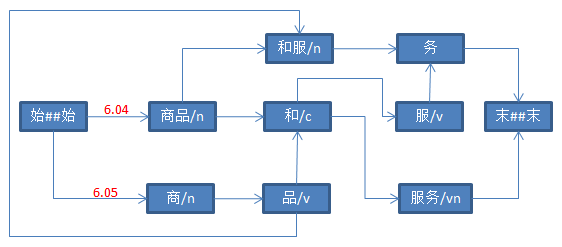
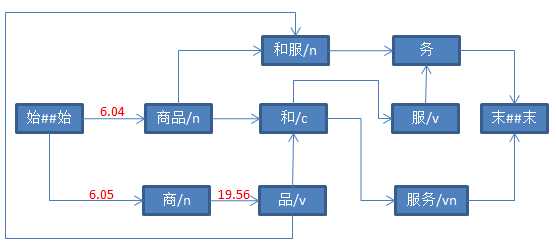
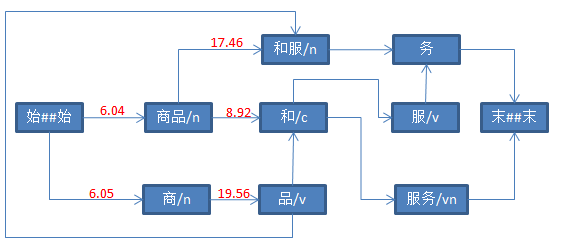
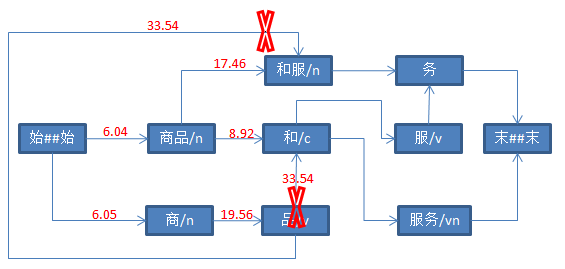
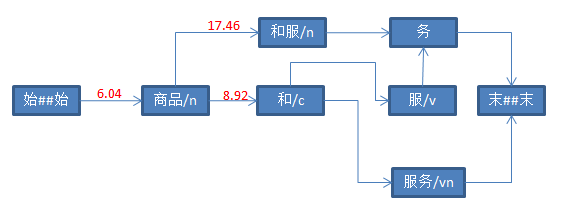
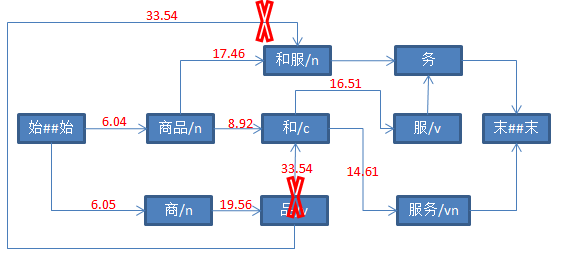
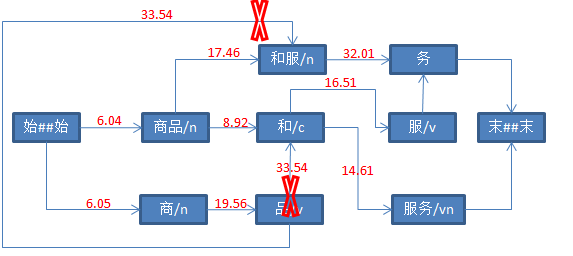
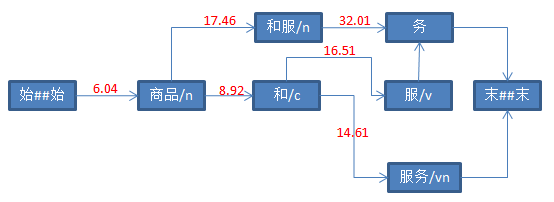

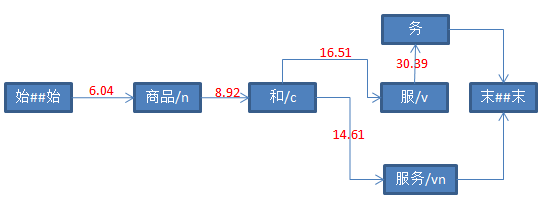

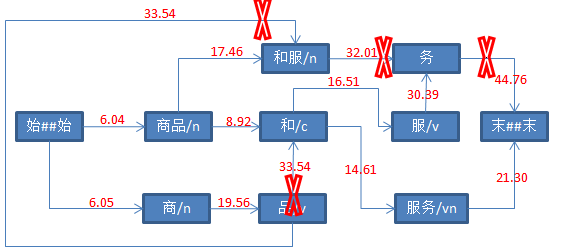
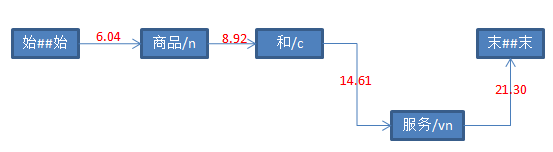
参考资料
ansj构造最短路径的更多相关文章
- ansj人名识别
1.前言 ansj人名识别会用到两个字典,分别是:person/asian_name_freq.data.person/person.dic. 1.1.asian_name_freq.data 这是一 ...
- 关于Floyd-Warshall算法由前趋矩阵计算出的最短路径反映出了算法的执行过程特性的证明
引言:Floyd-Warshall算法作为经典的动态规划算法,能够在O(n3)复杂度之内计算出所有点对之间的最短路径,且由于其常数较小,对于中等规模数据运行效率依然可观.算法共使用n此迭代,n为顶点个 ...
- 最短路径树:Dijstra算法
一.背景 全文根据<算法-第四版>,Dijkstra算法.我们把问题抽象为2步:1.数据结构抽象 2.实现 二.算法分析 2.1 数据结构 顶点+边->图.注意:Dijkstra ...
- cocos2d-js版本A*算法
[转]http://blog.csdn.net/realcrazysun1/article/details/43054229 A*算法的东西网上讲了很多~但还是不可避免的要去研究一下,cocos官网上 ...
- OSPF详解
OSPF 详解 (1) [此博文包含图片] (2013-02-04 18:02:33) 转载 ▼ 标签: 端的 第二 以太 第一个 正在 目录 序言 初学乍练 循序渐进学习OSPF 朱皓 入门之前 了 ...
- 树链剖分-点的分治(点数为k且距离最长的点对)
hdu4871 Shortest-path tree Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 130712/130712 K ( ...
- LeetCode--064--最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小. 说明:每次只能向下或者向右移动一步. 示例: 输入:[ [1,3,1], [1,5,1], ...
- Dijkstra算法构造单源点最短路径
迪杰斯特拉(Dijkstra)算法 是求从某个源点到其余各顶点的最短路径,即对已知图 G=(V,E),给定源顶点 s∈V,找出 s 到图中其它各顶点的最短路径. 我总结下核心算法,伪代码如下: Dij ...
- BZOJ 4016 最短路径树问题 最短路径树构造+点分治
题目: BZOJ4016最短路径树问题 分析: 大家都说这是一道强行拼出来的题,属于是两种算法的模板题. 我们用dijkstra算法算出1为源点的最短路数组,然后遍历一下建出最短路树. 之后就是裸的点 ...
随机推荐
- 图像边缘检测--OpenCV之cvCanny函数
图像边缘检测--OpenCV之cvCanny函数 分类: C/C++ void cvCanny( const CvArr* image, CvArr* edges, double threshold1 ...
- XMPP系列(二)----用户注册和用户登录功能
1.创建一个新工程 2.导入XMPP框架 最新的XMPP框架下载地址:https://github.com/robbiehanson/XMPPFramework 将XMPP的几个文件夹拖进工程中,需要 ...
- 猴子吃桃问题---C实现
原题:猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了了一个.第二天早上又将剩下的桃子吃掉一半,又多吃了一个.以后每一天早上都吃前一天剩下桃子的一半零一个.到第十天早上想再吃时,发现 只剩下 ...
- 从开发者角度解析 Android N 新特性!
大清早看到 Google 官方博客发布 Android N 的开发者预览版,立马从床上跳起来开始仔仔细细的读起来. 从开发者角度来看,Android N 的更新并不算大.网上之前流传的一些 Andro ...
- MASM中3中文本宏的使用与区别
= 宏 格式 : name = exp 其中,exp只能为32位整数值,且用=宏定义的符号名称可以重定义: EQU 宏 格式1:name EQU exp exp为有效整数值,可以重定义: 格式2:na ...
- css选择器应用
.mynav li:not(:last-child) { margin-right: 20px; }
- Windows上模拟Linux环境的软件Cygwin
Windows上模拟Linux环境的软件Cygwin 2010-10-11 15:19 我要评论(0) 字号:T|T Cygwin是一个用于在Windows上 模拟Linux环境的软件.它可 ...
- 关于非现场审计软件的一些介绍(ACL、IEDA、Teammate)
http://group.vsharing.com/Article.aspx?aid=661512 IDEA是由caseware开发的数据分析软件.caseware的网址如下:http://www.c ...
- SQL Server复制表结构和表数据生成新表的语句
参考:http://topic.csdn.net/t/20020621/09/820025.html SELECT * INTO newTableName FROM oldTabl ...
- 体育Bank2016会议笔记
补注:会议全称应该是体育Bank2016体育投融资总裁年会 新华社体育部徐仁基 演讲主题:帮郭川找到大海-->帮民众找到自己真正的体育爱好 激发和培养体育市场是重中之重 将体育培养成生活习惯.生 ...
