吴恩达深度学习笔记（deeplearning.ai）之卷积神经网络（二）

经典网络

1. LeNet-5
2. AlexNet
3. VGG

• Ng介绍了上述三个在计算机视觉中的经典网络。网络深度逐渐增加，训练的参数数量也骤增。AlexNet大约6000万参数，VGG大约上亿参数。

• 从中我们可以学习到随着网络深度增加，模型的效果能够提升。另外，VGG网络虽然很深，但是其结构比较规整。每经过一次池化层（过滤器大小为2，步长为2），图像的长度和宽度折半；每经过一次卷积层，输出数据的channel数量加倍，即卷积层中过滤器（filter）的数量。

残差网络（ResNet）

• 由于存在梯度消失与梯度爆炸的现象，很难训练非常深的网络，因此引入了 “skip connections ”的概念，它可以从网络中的某一层获取激活值，并将信息传递给更深一层的网络（通过级联操作，将输入流合并），残差块可以训练更深的神经网络。

• 残差网络的结构如下：
  
  

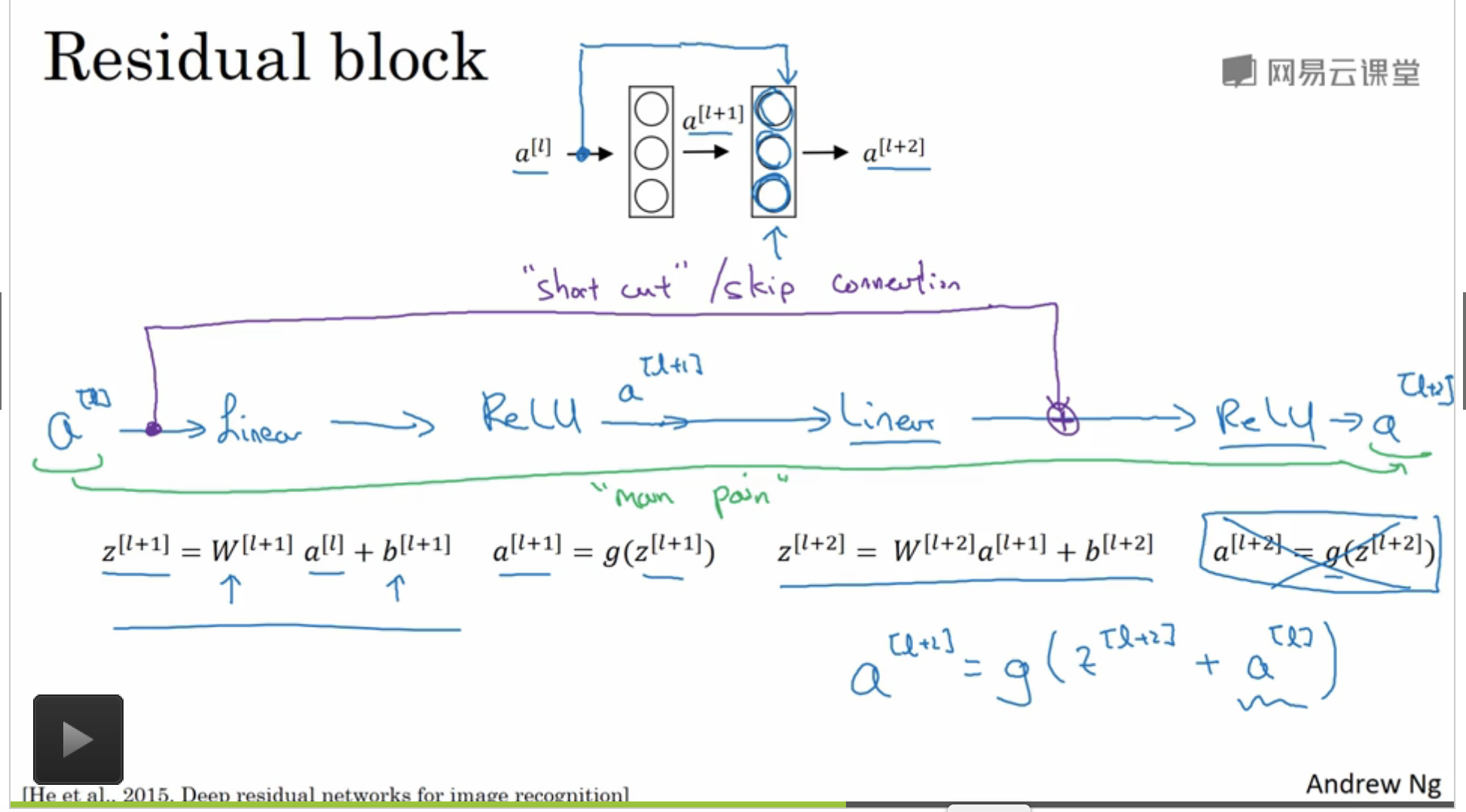
• 更加直观的理解是，残差网络可以尽量避免梯度爆炸或消失的现象；

• 我认为级联相当于对网络加了双层保险，类似于物理中电路的并联，两个输入流只要有一个work，仍能使网络正常训练。