1.6 dropout正则化

　　除了L2正则化，还有一个非常实用的正则化方法----dropout（随机失活），下面介绍其工作原理。

假设你在训练下图左边的这样的神经网络，它存在过拟合情况，这就是dropout所要处理的。我们复制这个神经网络，dropout会遍历网络每一层，并设置一个消除神经网络中节点的概率。

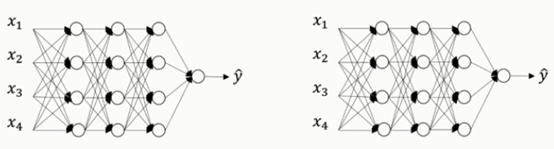
　　假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点之后，我们会消除一些节点，然后删掉从该节点进出的连线，如下图，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。对于每个训练样本（每一个mini-batch），我们都将重复上述操作，以一定的概率消除网络节点，得到一个精简后的神经网络，然后训练这个神经网络。

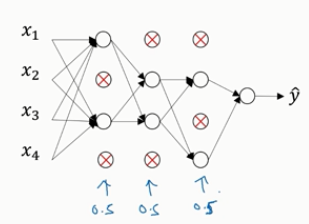
如何实施dropout呢？方法有几种，下面介绍最常见的，即inverted dropout（反向随机失活）。

下面我们用一个三层（L=3）的网络来举例说明。下面只举例说明如何在某一层中实施dropout。

首先要定义向量d，对d3表示第三层的dropout向量。

d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob

看d3是否小于某个数keep_prob，keep_prob是一个具体数字，上面的示例中它是0.5，本例中设置keep_prob=0.8，它表示保留某个隐藏单元的概率，即此处意味着消除任意一个隐藏单元的概率是0.2。 它的作用是生成随机矩阵，如果对a3进行因子分解，效果也是一样的。d3是一个矩阵，其中d3中值为1的概率都是0.8，值为0的概率是20%。接下来要做的就是从第三层中获取激活函数，这里我们叫它a3，a3含有要计算的激活函数

a3=np.multiply(a3, d3)     #a3*=d3

注：上面是对应元素相乘

它的作用就是过滤d3中所有等于0的元素。而各个元素等于0的概率只有20%，乘法运算最终把a3中相应的元素归零。

如果用python实现的话，d3就是一个布尔型数组，值为true或者false，而不是1或0。乘法运算依旧有效，python会把true和false翻译为1和0

最后我们向外扩展a3，即除以keep_prob参数

a3 /= keep_prob   #所谓的dropout方法，功能是不论keep_prob的值时多少，反向随机失活(inverted dropout)方法通过除以keep_prob，以确保a3的期望值不变。

下面解释为什么要这么做

方便起见，假设第三层隐藏层有50个神经元，在一维上a3是50，我们通过因子分解将它拆分成50xm维的，保留和删除它们的概率分别是80%和20%，这意味着最后被删除或者归零的神经元平均有10个。

我们现在看看z4

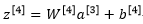
我们的预期是a3减少20%，也就是说a3中有20%的元素被归零，为了不影响z4的期望值，我们需要用w4*a3除以0.8，它将会修正或者说弥补我们所需的那20%，因此a3的期望值不会变。

事实证明，在测试阶段，当我们评估一个神经网络时，inverted dropout使得测试阶段变得更容易，因为它的数据扩展变得更容易。

目前实施dropout最常用的方法就是Inverted dropout

现在你使用的是d向量，你会发现不同的训练样本，清除不同的隐藏单元也不同，事实上，如果你通过相同训练集多次传递数据，每次训练数据的梯度不同，则随机对不同隐藏单元归零。

向量d或者d3用来决定第三层中哪些单元归零，无论在前向传播还是在反向传播的时候

如何在测试阶段训练算法？

在测试阶段，我们已经给出了x或者想预测变量，用的是标准计数法，a0表示第0层的激活函数标注为测试样本x，我们在测试阶段不使用dropout函数，尤其是像下面这种情况：

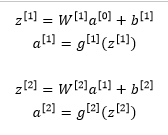
以此类推，直到最后一层预测值为y’

显然，在测试阶段，我们并没有使用dropout，自然也不需要随机将神经元失活，因为在测试阶段进行预测时，我们不期望输出的结果是随机的，如果在测试阶段应用dropout函数，预测会受到干扰，理论上，你只需要多次运行预测处理过程，每一次不同的隐藏单元会被随机归零，遍历它们并进行预测处理，这样得出的结果也几乎相同，但是计算效率低。

Inverted dropout函数除以keep_prob（ /=keep_prob ）这一操作，目的是确保即使是在测试阶段不执行dropout来调整数值范围，激活函数的预期结果也不会发生变化，所以没有必要在测试阶段额外添加尺度参数，这与训练阶段不同

内容主要来自与：

Andrew Ng的改善深层神经网络：超参数调试、正则化以及优化课程