2016弱校联盟十一专场10.2---Around the World（深搜+组合数、逆元）

题目链接

https://acm.bnu.edu.cn/v3/problem_show.php?pid=52305

problem  description

In ICPCCamp, there are n cities and (n−1) (bidirectional) roads between cities. The i-th road is between the ai-th and bi-th cities. It is guaranteed that cities are connected. Recently, there are 2×ci −1 new roads built between the ai-th and bi-th cities. Bobo soon comes up with an idea to travel around the world! He plans to start in city 1 and returns to city 1 after traveling along every road exactly once. It is clear that Bobo has many plans to choose from. He would like to find out the number of different plans, modulo (109 + 7). Note that two plans A and B are considered different only if there exists an i where the i-th traveled road in plan A is different from the i-th road in plan B.

Input

The first line contains an integer n (2 ≤ n ≤ 105 ). The i-th of the following (n − 1) lines contains 3 integers ai , bi , ci (1 ≤ ai , bi ≤ n, ci ≥ 1, c1 + c2 + · · · + cn−1 ≤ 106 ).

Output

An integer denotes the number of plans modulo (109 + 7).

Examples

standard input

3

1 2 1

2 3 1

3

1 2 1

1 3 2

standard output

4

144

题意：输入n 表示由n个节点构成的树，然后输入n-1条边，n-1行每行输入ai bi c 表示ai点和bi点之间有2*c条边相连，现在求从1号点开始走完所有边且每条边只走一次的方案数？

思路：深搜，然后排列组合，举两个例子：

        

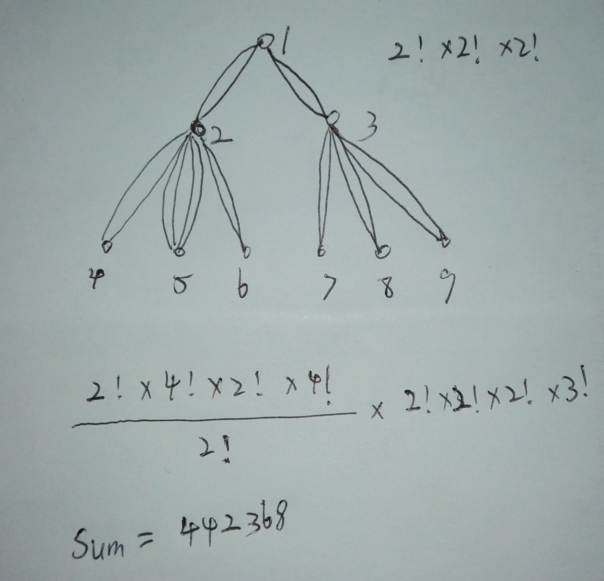
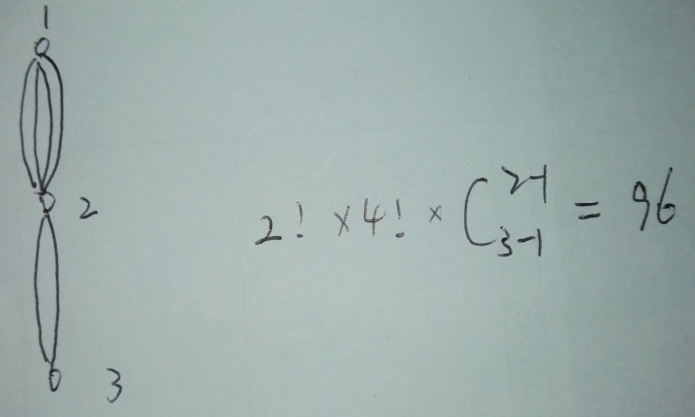
第一个图片中：定义sum=1，从1号点开始向下深搜，到达孩子2号点的时候sum*=2！  表示从1到2号点走遍边的方法数，然后继续向下深搜到4号点，sum*=2！  然后返回再到5号点，sum*=4！ 再返回走到6号点，sum*=2！ ，然后返回2号点，这时sum*=4！/2！ 为什么呢？ 因为从2号点开始走完它的直系（儿子）孩子节点时，它的儿子路径之间存在先后顺序，所以乘上路径数的阶乘，但要除去重复的部分比如从2号点到5号点时这两条路径的先后顺序在之前的4！中已经考虑了，接下来就是相同的过程了......注意的是下面的孩子节点算完了，再计算上层节点时就不需要考虑了，但是相邻两层的节点之间还是有影响的，这个图看不出来，我用下面一个图作解释。

第二个图片中：按照之前的算法为sum=4！*2！=48  其实正确的解是96  ，少乘了一个2，为什么呢？ 因为上面一层的路径对下面一层的路径产生了影响，上一层有两条路径，下面一层只有一条路径，那么可以分析存在两种情况：1、  1->2->3->2->1->2->1         2、  1->2->1->2->3->2->1   怎么产生的？ 其实是在走上一层的路径时，在哪一次走的这一层的路径，用挡板法，设上一层有t条路径，这一层有s条路径，那么得在t次把下面的s条路径走完，也就是C（t+s-1，t-1） 。

代码如下：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
typedef long long LL;
const LL maxn=1e5+;
const LL mod=1e9+;
using namespace std;
struct Tree
{
    LL to,next,c;
} edge[maxn*];
LL Inv[*maxn];
LL tot,head[maxn];
LL jc[maxn*];
LL sum;
void Init()
{
    Inv[]=;
    Inv[] = ;
    for(LL i=; i<*maxn; i++)
        Inv[i] = (mod-mod/i)*Inv[mod%i]%mod;
    for(LL i=; i<*maxn; i++)
        Inv[i] = (Inv[i-]*Inv[i])%mod;
}
void init()
{
    tot=;
    memset(head,-,sizeof(head));
}
void add_edge(LL u,LL v,LL c)
{
    edge[tot].to=v;
    edge[tot].c=c;
    edge[tot].next=head[u];
    head[u]=tot++;
}

void init2()
{
    jc[]=;
    for(LL i=; i<maxn*; i++)
        jc[i]=((jc[i-]*i)%mod);
}
LL road[maxn];
void  dfs(LL u,LL pre)
{
    road[u]=;
    for(LL i=head[u]; i!=-; i=edge[i].next)
    {
        LL v=edge[i].to;
        if(v==pre) continue;
        dfs(v,u);
        road[u]+=edge[i].c;
        sum=(((sum*jc[edge[i].c*])%mod)*Inv[edge[i].c])%mod;
        sum=((sum*  jc[(road[v]+edge[i].c-)]%mod)*Inv[edge[i].c-] )%mod;
        sum=(sum*Inv[road[v]])%mod;
    }
    sum=(sum*jc[road[u]])%mod;
}

int main()
{
    Init();
    init2();
    LL n,u,v,c;
    while(scanf("%lld",&n)!=-)
    {
        sum=;
        init();
        for(LL i=; i<n; i++)
        {
            scanf("%lld%lld%lld",&u,&v,&c);
            add_edge(u,v,c);
            add_edge(v,u,c);
        }
        dfs(,);
        printf("%lld\n",sum);
    }
    return ;
}