CS231-Multi-calss SVM的求导

接着上周的更，上周我们更到，在对图像的线性分类中，我们只用multi-class 的svm，然后我们得到以下的损失函数

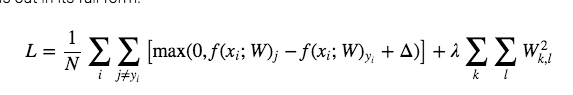
这里每个数值代表为下：

• X 是一个 N by D 的矩阵，N 代表 training data 的数量，D 代表每个 training data 的维度
• W 是一个 D by C 的矩阵，C 代表 class 的数量
• i 迭代 N 个 training data
• j 迭代 C 个 class
•  是 margin parameter

这里，我们想通过一个方法来得到损失函数L的最小值，方法很多，但是这里，考虑使用计算w的梯度来不停的对L进行优化，这里想的就是初始化一个W，然后计算W的梯度，接着不停的迭代W，直到收敛或者达到迭代次数。

那接着问题就是如何求L对于W的梯度了。

这里我们先不考虑后面的正则项，因为那个就是lambda w，一眼就求完了，求前面的就可以了。

那么，我们先把L给拆分一下，这样可以去掉一个求和符号

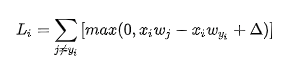
这里我们来拆解一下情况，如果后面一项小于或者等于0的时候，那这个导数就直接是0，我们主要考虑后面一项大于0的情况

首先j != yi

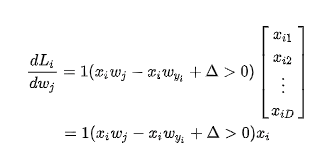
如果说j = yi

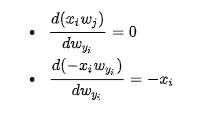
所以这里面

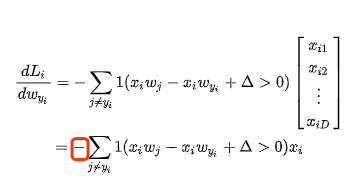
这里面我们需要用一个indicator 1 来判断符号，看起来比较复杂，但是可能代码里面会比较简单

接着我们把这N个样本的loss给sum起来就完事了。

周末回家了，没来及撸代码，下周更新代码。