【枚举Day1】20170529-2枚举算法专题练习 题目

20170529-2枚举算法专题练习

题解： http://www.cnblogs.com/ljc20020730/p/6918360.html

青岛二中日期	序号	题目名称	输入文件名	输出文件名	时限	内存	算法	难度	分类
081113	1	最大矩形	rectangle.in	rectangle.out	1s	256MB	枚举	1	02枚举
081031	2	回文	palin.in	palin.out	1s	256MB	枚举、优化	1	02枚举
081008	3	问题的设置	problemsetter.in	problemsetter.out	1s	256MB	排序+枚举	1	02枚举
081031	4	矩形着色	rectangles.in	rectangles.out	1s	256MB	枚举	2	02枚举

1.OneMoreRectangle一个矩形

【题目描述】

在一个平面上有一些矩形。矩形的边都与坐标轴平行。矩形允许相交、重叠。你的任务是，在平面上再放入一个边与坐标轴平行的矩形，且覆盖尽量多的已有矩形。

我们用四个整数来表示一个矩形，x1,y1,x2,y2，分别表示矩形的横纵坐标最小值、横纵坐标最大值。若矩形a的坐标为x1,y1,x2,y2，矩形A的坐标为X1,Y1,X2,Y2，则a能被A覆盖当且仅当X1<=x1<x2<=X2，且Y1<=y1<y2<=Y2。

【输入文件】第一行有三个整数n,X,Y，分别表示已有矩形个数、你要放入的矩形的边长（也就是X=X2-X1,Y=y2-y1）。你放入的矩形的大小必须同规定大小相同，位置由你决定。

接下来n行，每行4个整数x1,y1,x2,y2，表示已知矩形的坐标。

【输出文件】只有一个整数，表示你最多可以覆盖几个已有矩形。

【输入样例】

3 2 2

1 1 2 2

2 2 3 3

3 3 4 4

【输出样例】2

【数据规模和约定】

n<=50；

所有给定坐标的绝对值不超过10⁹；

所有给定坐标保证x1<x2，y1<y2；

X和Y是不超过10⁹的正整数。

2.Palindromes回文

【题目描述】一个回文串指的是，左右翻转后同原串相同的串。

给定一个数k(2<=k<=30000)和一个非空字符串S，S的长度不超过30000且只含小写字母。请你求出，S中有多少个不同的长度为k的回文子串。一个串的子串指的是它的连续的一部分。

本题中，两个长度为k的子串不同，当且仅当它们的起始位置不同。

【输入文件】第一行整数k。

第二行串S。

【输出文件】一个整数，表示不同的回文串个数。

【输入样例】

5

ababab

【输出样例】2

3.ProblemSetter(问题的设置)

【题目描述】

你要为一场比赛出题。从已有的题目中，你要选择三道不同的题：一道简单题、一道中等题，以及一道难题。每道题目都有一个整数的难度值。值越大，题目越难。假设E表示你选择的简单题的难度，M表示中等题难度，H表示难题难度，则必须保证E<=M<=H。你希望难度差尽量接近，也就是说，假设D1=M-E，D2=H-M，则|D1-D2|应该最小。如果有多种方案，选择其中E最小的。如果仍有多种方案，选择其中H最大的。如果还有多种方案，选择其中M最小的。

【输入文件】第一行一个整数n，表示题目数量。第二行n个整数，表示每道题的难度。

【输出文件】输出一行三个整数表示选择的题目难度。按照简单-中等-困难的顺序输出。中间用一个空格隔开。行尾不要有空格。

【输入样例】

5

1 2 3 4 5

【输出样例】

1 3 5

【样例说明】

此时，D1=D2=2。

【数据规模和约定】

3<=n<=50

难度是不超过1000的正整数。

4.ColoringRectangles着色的矩形

【题目描述】

在平面中给定N个与坐标轴平行的矩形，第i个矩形的左下角坐标是(x₁[i],y₁[i])，右上角坐标是(x₂[i],y₂[i])。

你的任务是从中选择K个矩形，使得所选矩形可视面积最大。如果一些矩形有重叠，那么重叠部分只有编号最大的矩形才可视。换句话说，编号大的矩形“盖”在编号小的矩形之上。请你输出选择的K个矩形的编号。如果有多种方法，输出字典序最小的一组。

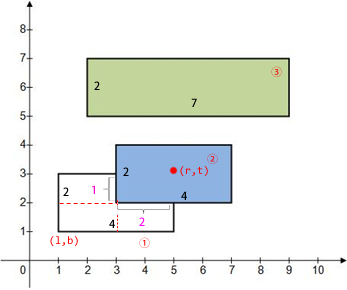
【输入文件】

第一行两个整数N,K。

第二行N个整数，表示x1[0]..x1[N-1]。

第三行N个整数，表示y1[0]..y1[N-1]。

第四行N个整数，表示x2[0]..x2[N-1]。

第五行N个整数，表示y2[0]..y2[N-1]。

【输出文件】

一行K个非负整数，表示选择的矩形的编号。编号之间用一个空格隔开。

【输入样例】

3 2

1 3 2

1 2 5

5 7 9

3 4 7

【输出样例】

1 2

【样例说明】

选择矩形0,1，面积为6+8=14

选择矩形0,2，面积为6+14=20

选择矩形1,2，面积为8+14=22。

【数据规模和约定】

1<=N<=50

-10000<=所有坐标<=10000

对于任意i，x1[i]<x2[i],y1[i]<y2[i]