python 实现二叉树的深度 & 广度优先遍历

什么是树

在计算器科学中，树（英语：tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。

树的特点

​ 每个节点有零个或多个子节点；

​ 没有父节点的节点称为根节点；

​ 每一个非根节点有且只有一个父节点；

​ 除了根节点外，每个子节点可以分为多个不相交的子树

概念

​ 节点的度：一个节点含有的子树的个数称为该节点的度；

​ 树的度：一棵树中，最大的节点的度称为树的度；

​ 叶节点或终端节点：度为零的节点；

​ 非终端节点或分支节点：度不为零的节点；

​ 父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

​ 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

​ 兄弟节点：具有相同父节点的节点互称为兄弟节点；

​ 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

​ 深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0；

​ 高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；

​ 堂兄弟节点：父节点在同一层的节点互为堂兄弟；

​ 节点的祖先：从根到该节点所经分支上的所有节点；

​ 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。

​ 森林：由m（m>=0）棵互不相交的树的集合称为森林；

什么是二叉树

二叉树：每个节点最多含有两个子树的树称为二叉树；

完全二叉树：对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；

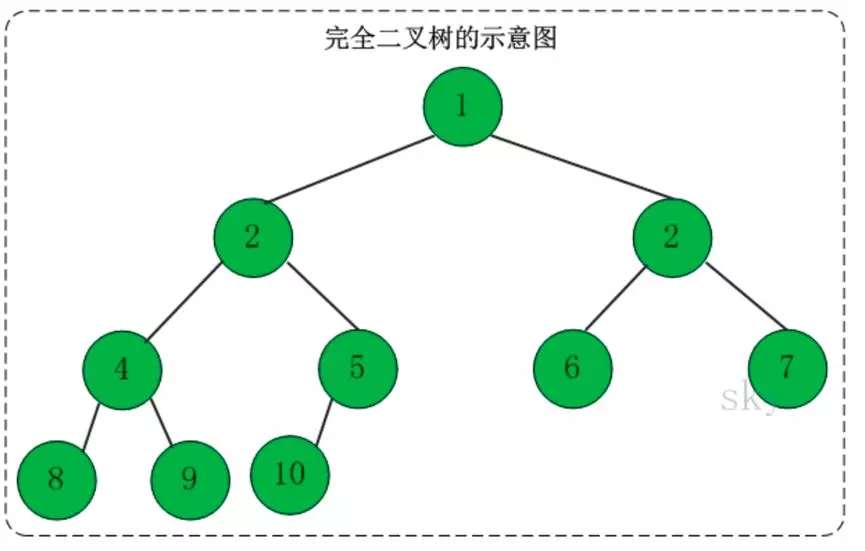
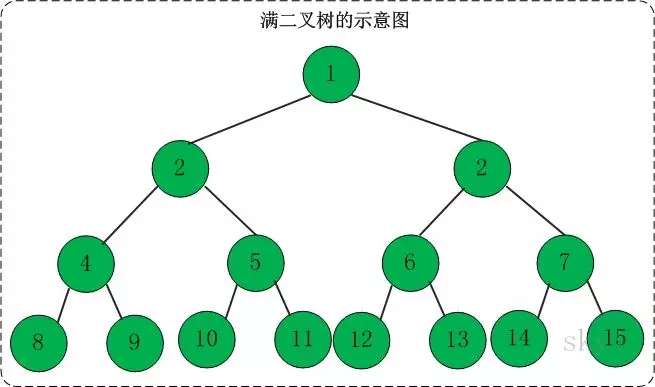
满二叉树：所有叶节点都在最底层的完全二叉树；

深度优先

深度优先遍历即是先按深度来遍历二叉树，包括：

前序遍历

遍历顺序 --> 根节点 -> 左子树 -> 右子树

中序遍历

遍历顺序--> 左子树 -> 根节点 -> 右子树

后序遍历

遍历顺序--> 左子树 -> 右子树 -> 根节点

# 定义一个树节点
class TreeNode:
    def __init__(self, value=None, left=None, right=None):
        self.value = value
        self.left = left     # 左子树
        self.right = right   # 右子树

# 实例化一个树节点
node1 = TreeNode("A",
                 TreeNode("B",
                          TreeNode("D"),
                          TreeNode("E")
                          ),
                 TreeNode("C",
                          TreeNode("F"),
                          TreeNode("G")
                          )
                 )

# 前序遍历
def preTraverse(root):
    if root is None:
        return
    print(root.value)
    preTraverse(root.left)
    preTraverse(root.right)

# 中序遍历
def midTraverse(root):
    if root is None:
        return
    midTraverse(root.left)
    print(root.value)
    midTraverse(root.right)

# 后序遍历
def afterTraverse(root):
    if root is None:
        return
    afterTraverse(root.right)
    afterTraverse(root.left)
    print(root.value)

if __name__ == "__main__":
    preTraverse(node1)
    print("------------------------")
    midTraverse(node1)
    print("------------------------")
    afterTraverse(node1)

# 运行结果
----------前序遍历--------------
A
B
D
E
C
F
G
----------中序遍历--------------
D
B
E
A
F
C
G
----------后序遍历--------------
G
F
C
E
D
B
A

广度优先

广度优先遍历即是层次遍历，按一层一层地遍历。

def levelOrder(root):
    # 如果根节点为空，则返回空列表
    if root is None:
        return res
    # 模拟一个队列储存节点
    q = []
    # 首先将根节点入队
    q.append(root)
    # 列表为空时，循环终止
    while len(q) != 0:
        length = len(q)
        for i in range(length):
            # 将同层节点依次出队
            r = q.pop(0)
            if r.left is not None:
                # 非空左孩子入队
                q.append(r.left)
            if r.right is not None:
                # 非空右孩子入队
                q.append(r.right)
            print(r.value)
if __name__ == "__main__":
    levelOrder(node1)

运行结果

A
B
C
D
E
F
G