poj3162（树形dp+优先队列）

Walking Race

Time Limit: 10000MS		Memory Limit: 131072K
Total Submissions: 5409		Accepted: 1371
Case Time Limit: 3000MS

Description

flymouse’s sister wc is very capable at sports and her favorite event is walking race. Chasing after the championship in an important competition, she comes to a training center to attend a training course. The center has N check-points numbered 1 through N. Some pairs of check-points are directly connected by two-way paths. The check-points and the paths form exactly a tree-like structure. The course lasts N days. On the i-th day, wc picks check-point i as the starting point and chooses another check-point as the finishing point and walks along the only simple path between the two points for the day’s training. Her choice of finishing point will make it that the resulting path will be the longest among those of all possible choices.

After every day’s training, flymouse will do a physical examination from which data will obtained and analyzed to help wc’s future training be better instructed. In order to make the results reliable, flymouse is not using data all from N days for analysis. flymouse’s model for analysis requires data from a series of consecutive days during which the difference between the longest and the shortest distances wc walks cannot exceed a bound M. The longer the series is, the more accurate the results are. flymouse wants to know the number of days in such a longest series. Can you do the job for him?

Input

The input contains a single test case. The test case starts with a line containing the integers N (N ≤ 10⁶) and M (M < 10⁹). Then follow N − 1 lines, each containing two integers f_i and d_i (i = 1, 2, …, N − 1), meaning the check-points i + 1 and f_i are connected by a path of length d_i.

Output

Output one line with only the desired number of days in the longest series.

Sample Input

3 2
1 1
1 3

Sample Output

3

Hint

Explanation for the sample:

There are three check-points. Two paths of lengths 1 and 3 connect check-points 2 and 3 to check-point 1. The three paths along with wc walks are 1-3, 2-1-3 and 3-1-2. And their lengths are 3, 4 and 4. Therefore data from all three days can be used for analysis.

Source

POJ Monthly--2006.12.31, flymouse

 

题意：给你一颗有n个节点的树，wc跑n天步，第i天从第i个节点出发，在该天选一个点为终点，在不折回跑的情况下，使得跑的路程最远。问选一段连续时间，在这些天内跑的路程最大值最小值差不超过m的条件下，最长的连续天数。

思路：看到这道题，很明显的树形dp的问题，我们可以先随便令一个点为根节点，先进行一次dfs算出在这基础下每个节点可以走的最大距离和次大距离，然后以这些算出的最大距离和次大距离再进行一次dfs算出以该点出发，可以走的最大距离。     

对于样例：

12 6
1 2
2 4
2 2
1 6
1 5
6 1
6 1
7 2
7 3
10 1
11 4

第一次dfs遍历后可以得到下图的数据（该点不同分支的最长距离，该点不同分支的次长距离）    

我们可以发现，当前点的最大长度（对于整颗树而言）取值有两种

红色路线为6号节点由第一次dfs求出的最长距离

绿色路线为1号节点由第一次dfs求出的最长距离

橙色路线为1号节点由第一次dfs求出的次长距离

1号节点为6号节点的父亲

 

以6号节点为例，一种是红线往下走的那种，还有一种是走黄线往上走回到它父亲然后选择父亲节点的最长路走或者次长路走

（如果当前节点就处于它父亲节点的最长路上，那么我们回到父亲节点时就只能走父亲节点的次长路，反之就可以走父亲节点的最长路，由此我们就可以算出6节点实际上可以走的最远距离）

对于6号节点，很显然它处于它父亲节点1的最长路上（绿色的线路），所以当它回到父亲节点时就只能走次长路（橙色的线路）。

最终实际最长距离取往父亲节点走（黄+橙色）（具体走橙色路线还是绿色路线以上面括号里的要求而定）和往自己的最长路走（红色路线）的中最大的那个

这里有点要注意的，当你求出了一个点的实际最长距离，并且该最长距离是往父亲节点走而获得的，那么我们要更新最长距离和次长距离

 

求出所有节点的实际最长距离后，我们就可以用优先队列或线段树来求出题目所需的最长连续天数了（本博客使用的是优先队列）

 

代码

 

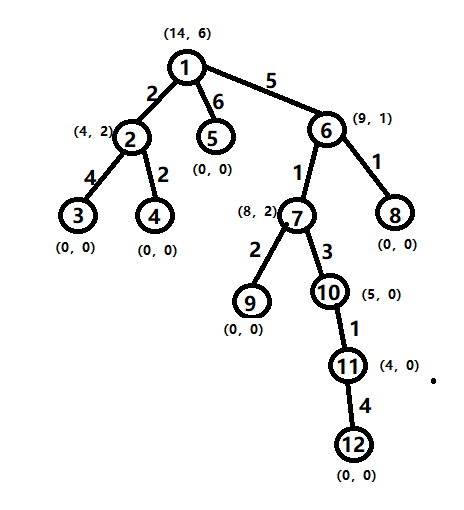
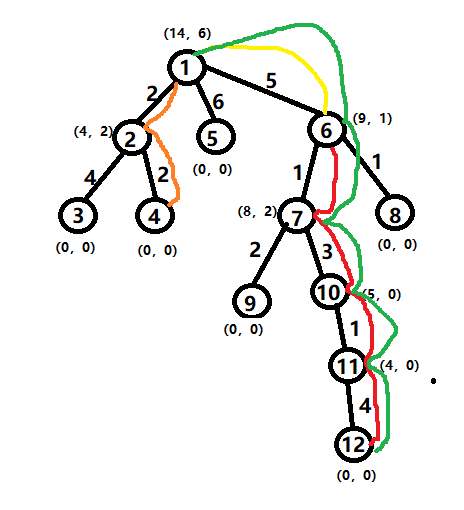
#include<cstdio>
#include<algorithm>
#include<queue>
#define ll long long
using namespace std;
struct{
	int v,w,next;
}edge[2000010];//前向星存树
int head[1000010];
int cnt;
deque<ll> mx,mn;//双向队列求连续天数
struct{
	ll lfst;//最长距离
	ll lsnd;//次长距离
}dp[1000010];
ll ans[1000010];//存实际最长距离
void add(int u,int v,int w){//加边
	edge[cnt].v=v;
	edge[cnt].w=w;
	edge[cnt].next=head[u];
	head[u]=cnt++;
}

void dfs1(int k,int fz){//（当前节点，父亲节点）
	//printf("%d\n",k);
	for(int i=head[k];i!=-1;i=edge[i].next){
		int v=edge[i].v;
		if(v==fz)
		continue;
		dfs1(v,k); //先往下递归
		ll a=dp[v].lfst+edge[i].w;
		if(a>dp[k].lfst){//更新最长，次长距离
			dp[k].lsnd=dp[k].lfst;
			dp[k].lfst=a;
		}
		else if(a>dp[k].lsnd)
		dp[k].lsnd=a;
	}
}
void dfs2(int k,int fz,int w){//（儿子节点，根节点，儿子节点到根节点的距离）
		//printf("wwww%d %d %d %d\n",k,fz,dp[fz].lfst,dp[fz].lsnd);
		if(dp[k].lfst+w==dp[fz].lfst){//如果当前节点在其父亲节点的最长距离线路上
			ll a=w+dp[fz].lsnd;//尝试走父亲节点的次长距离
			if(a>dp[k].lfst){
				dp[k].lsnd=dp[k].lfst;
				dp[k].lfst=a;
			}
			else if(a>dp[k].lsnd)
			dp[k].lsnd=a;
			ans[k]=dp[k].lfst;
		}
		else{
			ll a=w+dp[fz].lfst;//尝试走父亲节点的最长距离
			if(a>dp[k].lfst){//比较并更新
				dp[k].lsnd=dp[k].lfst;
				dp[k].lfst=a;
			}
			else if(a>dp[k].lsnd)
			dp[k].lsnd=a;
			ans[k]=dp[k].lfst;//求出实际最长距离
		}
	for(int i=head[k];i!=-1;i=edge[i].next){
		int v=edge[i].v;
		if(v==fz)
		continue;
		dfs2(v,k,edge[i].w);
	}
}
void addmn(int k){//加入递增队列
	while(mn.size()&&(ans[mn.back()]>ans[k])){//保持加入节点后队列的单调性
		mn.pop_back();
	}
	mn.push_back(k);
}
void addmx(int k){//加入递减队列
	while(mx.size()&&(ans[mx.back()]<ans[k])){
		mx.pop_back();
	}
	mx.push_back(k);
}
int main(){
	int n,m;
	int v,w;
	cnt=0;
	scanf("%d%d",&n,&m);
	fill(head,head+n+2,-1);//初始化
	dp[0].lfst=dp[0].lsnd=0;
	dp[1].lfst=dp[1].lsnd=0;
	for(int i=2;i<=n;i++){
		scanf("%d%d",&v,&w);
		dp[i].lfst=dp[i].lsnd=0;//初始化
		add(i,v,w);
		add(v,i,w);
	}
	dfs1(1,0);
	ans[1]=dp[1].lfst;//我是以1根，那么1的实际最长距离就等于它的最长距离
	for(int i=head[1];i!=-1;i=edge[i].next){//往它的儿子节点遍历
		dfs2(edge[i].v,1,edge[i].w);//（儿子节点，根节点，儿子节点到根节点的距离）
	}
	mx.clear();
	mn.clear();
	mx.push_back(1);//先放入第一天
	mn.push_back(1);
	int len=0;
	int len1=1;
	int lf=1;//左标记，表示以第几天开始来计算
	for(int i=2;i<=n;i++){
		addmx(i);//将该天加入到队列里
		addmn(i);
		len1++;//长度加1
		while(lf<i&&len1&&abs(ans[mn.front()]-ans[mx.front()])>m){//如果绝对差大于m，那么开始天数要往右移
			len1--;//当前绝对差大于m，我们要尝试右移开始天数来使得绝对差变小
			if(mn.front()==lf)//如果当前的开始天数是最小的距离
			mn.pop_front();
			if(mx.front()==lf)//如果当前的开始天数是最大距离
			mx.pop_front();
			lf++;
		}
		len=max(len,len1);//更新答案
		//printf("wwwwwww%d %lld %lld %d\n",i,mn.front(),mx.front(),lf);
	}
	printf("%d\n",len);
	return 0;
}