与图论的邂逅03：Lengauer-Tarjan

　　回想一下，当我们在肝无向图连通性时，我们会遇到一个神奇的点——它叫割点。假设现在有一个无向图，它有一个割点，也就是说把割点删了之后图会分成两个联通块A,B。设点u∈A，v∈B，在原图中他们能够互相到达，而删了割点后他们就不能了。于是类似的，我们能不能够在有向图里面也找出这样的“割点”呢？也就是说，现在有两个点u,v，其中u可以到达v；而删去割点后，u不能再到达v。

　　在解决这个问题前，我们先吃一盘开胃菜——我们先给图中的边都取个名字。众所周知，用深度优先搜索遍历一张图，过程中走过的边和点会共同构成一棵树，它叫做这个图的搜索树。现在我们有一张有向图，我们找出它的搜索树之后，来观察一下这些边：

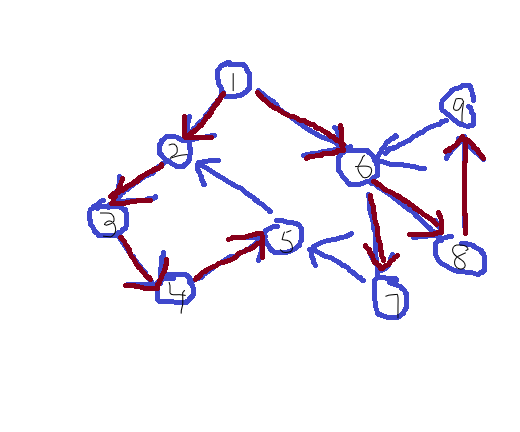
　　红色边和所连的点就是搜索树。画出这么一个玩意儿之后，我们给这些边都取个名字：

.树枝边：E(u,v)在搜索树中
.前向边：搜索树中连向v的边
.后向边：搜索树中v连出去的边
.横叉边：不在搜索树上的边

　　现在我们开始愉快地找规律。我们首先算出这些点的时间戳。假设图中每个点的时间戳都与自己的编号相同(假设是成立的)。先从树枝边开始，我们看E(1->2)并观察两个端点的时间戳，我们会发现，dfn[1]<dfn[2]；我们再观察E(2->3)，我们又发现dfn[2]<dfn[3]；我们再观察E(3->4)......观察完所有的树枝边，我们会发现一个规律：对于任意E(u->v)∈dfs tree，其中u∈V,v∈V，都有dfn[u]<dfn[v]。其实根据时间戳和搜索树的定义也是能够直接推出这个结论的。

　　由于前向边和后向边都是包含于树枝边的，我们现在先不管它。我们看看横叉边。E(5->2)就是横叉边，我们发现，dfn[5]>dfn[2]。那是不是对于任意E(u->v)∉dfs tree，其中u∈V,v∈V，都有dfn[u]>dfn[v]呢？看完图中所有横叉边之后，我们发现这个猜想仍然成立。但这是不是正确的结论呢？显然是的。下面来证一下，顺便加深一下我们对时间戳和搜索树的认识。

　　　　证明：假设我们搜索到了u，且图中存在E(u->v)，且v已经被搜索过，现在在搜索树中。设u的时间戳为dfn[v]，因为v已经被搜索过，所以E(u->v)不会加入到搜索树中，否则会形成环。易得出dfn[u]>dfn[v]，所以对于任意E(u->v)∉dfs tree，其中u∈V,v∈V，都有dfn[u]>dfn[v]。证毕。

　　好弱鸡的证明。。。但当时证这个的时候确实让我对时间戳和搜索树的认识加深了不少(其实还是我太弱了)。

---

　　看完这些乱七八糟的边之后，我们再整些点来玩(sang xin bing kuang)。

　　先看一下流图的定义：有向图G中，若存在一点r，从r出发能够到达图中所有的点，则称G为流图，记为(G,r)。

　　于是又有了一些新东西：

　　1.必经点。若(G,r)中r到v的所有路径都经过点u，则称u是v的必经点，记为u dom v(易懂吧)。v的所有必经点构成的集合记为dom(y)，dom(y)={x|x dom y}。

　　2.最近必经点。最接近v的必经点。首先，v的必经点的dfn肯定<v的dfn，在搜索树上越往上走，dfn越小。所以最接近v的必经点就是dom(v)中dfn最大的那个点。由于最近必经点唯一，可以记为idom(v)。

---

　　搞了这么大半天，我们到底要干些什么?!不清楚......啪！好吧，我们来给自己出一题：给定一张有向图(G,r)，求出对于每个点，有多少点以它为必经点。

　　考虑暴力怎么写。考虑特殊情况，我们认为dom(r)={r}。然后对于其余任意点v，考虑它的所有前驱节点的所有必经点。为了方便，我们设v的前驱节点集合为pre。设存在u1∈pre,u2∈pre，并且存在w dom u1。若|pre|=2，即v的前驱节点只有u1,u2，现有两种情况：w dom u2和!(w dom u2)。若是第一种情况，可以推出w同样是v的必经点；而第二种情况则w不是v的必经点。推广为|pre|>=2的情况，我们可以得出v的必经点集合就是v的所有前驱节点的必经点集合的交集，即∩_u∈predom(u)。于是我们得出了一种通过前驱节点来更新必经点的做法。所以我们可以从r开始往外算，若是DAG则根据拓补序计算，若是一般图则迭代一下。时间复杂度为O(N²)。但是连模板都跑不了。

　　那我们换一种思路求解。既然直接求出必经点太过突兀(?)，我们为何不通过求出一个弱鸡一点的东西，再进一步求出必经点呢？

　　所以我们再引入一个概念：

　　半必经点。能通过走非树枝边到达v的深度最小的v的祖先u。其实这个定义也没说清楚。假设u是v的半必经点，存在一条u到v的路径，把u和v都去掉后，路径上所有点的dfn都大于v的dfn。这样的u就是v的半必经点。当然，若路径上去掉u和v就没点了，那u就是v的半必经点。画个图：

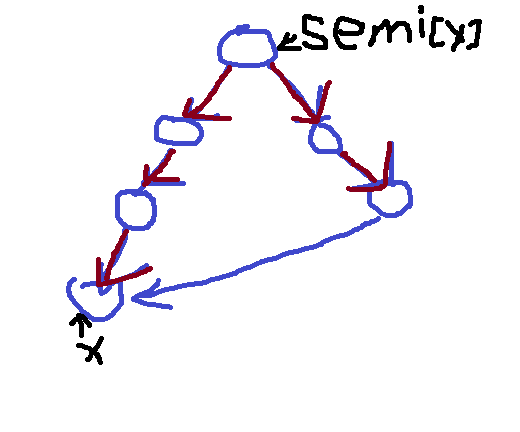
　   根据那个讲得不是很清楚的定义可以得出，一个点的半必经点是唯一的，u的半必经点记为semi(u)。

　　可以得出半必经点的一些性质：

1.x的半必经点一定是x在搜索树上的祖先，即dfn[semi[x]]<dfn[x].

2.半必经点不一定是必经点。

3.idom[x]是semi[x]在搜索树上的祖先(semi[x]也是自己的祖先)。

　　第一条是显而易见的。然后我们看第二条，假设半必经点就是必经点，下面给一个图推翻假设：

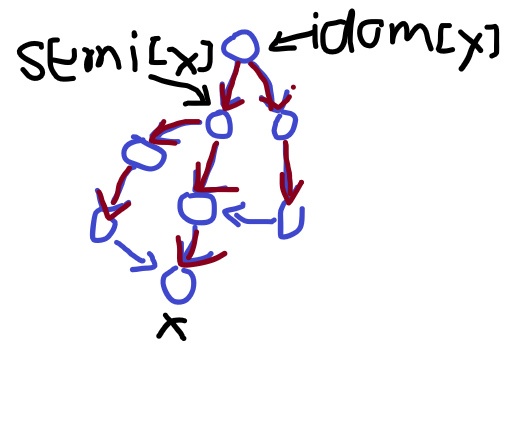
　　而第三条也是显然成立的，否则idom[x]就会位于semi[x]到x的路径上，而semi[x]到x的路径显然不止一条。

　　那么我们怎么求半必经点呢？

int tmp=+∞;
for(each v∈pre(u))
    if(dfn[v]<dfn[u]) tmp=min(tmp,dfn[v]);//E(v,u)为树枝边
    else for(each w∈anc(v)) if(dfn[w]>dfn[u])
        tmp=min(tmp,dfn[semi[w]]);//E(v,u)为横叉边
semi[u]=id[tmp];

　　这里的第二层for循环可以省掉。具体的做法是：用带权并查集来维护v的dfn最小的祖先，其权值就是dfn的值，用路径压缩可以达到logN级别，再加上按秩合并可以达到α(N)级别，增长率比log还慢，接近线性。然而我太弱了，只会打路径压缩。。。那么求出所有点的半必经点的时间复杂度就是0(NlogN)。

　　然而这只是半必经点而已，并不是必经点。所以我们还要通过半必经点来求出必经点。其实是求出最近必经点。

---

　　那么最近必经点怎么求呢？设semi[x]到x的路径上去掉了semi[x]之后的点构成的集合为path。

int y=id[min{dfn[semi[z]]|z∈path}];
if(semi[x]==semi[y]) idom[x]=semi[x];
else idom[x]=idom[y];

---

　　那么这两个东西的求法怎么证呢？(太弱了证不出来)这一块等层次练高了再补上。

---

　  然后就该解决问题了。我们来看一个神奇的东西：支配树。

　　支配树：从每个点的最近必经点往它连一条有向边。由于每个点的最近必经点是唯一的，所以新连的边和原图的点就构成了一棵树。这棵树叫支配树。也就是说树上的点支配着它的子树嘛。支配树中存在E(u,v)当且仅当u=idom(v)。树中存在u到v的路径当且仅当u dom v。

　　所以我们可以先求出有向图的支配树，那么对于一个点，它是多少点的必经点就等于它在支配树中有多少儿子了。怎么求呢？求支配树有一个算法，由Lengauer和Tarjan提出，那名字当然叫Lengauer-Tarjan啦~这个算法的原理是：

　　　　1.建出搜索树并算出每个点的时间戳

　　　　2.根据半必经点定理按时间戳从大到小计算出每个点的半必经点

　　　　3.根据必经点定理，通过算出的半必经点得出每个点的最近必经点

　　具体的过程：

　　　　1.每计算一个点时，把这个点放进生成森林中，用并查集维护

　　　　2.根据半必经点定理，若dfn[x]>dfn[y]，计算semi[y]时则需要考虑x祖先中dfn大于y的点

　　　　3.由于按时间戳从大到小的顺序计算，比y时间戳小的点还未加入生成森林，所以直接在生成森林中考虑x的祖先即可

　　　　4.令dfn[semi[x]]为x到其父亲的边的权值，用带权并查集可以求出边权的最小值

---

　　于是代码就能写得出来：

#include <stdio.h>
#include <string.h>
#define maxn 200001
#define maxm 300001

struct graph{
    struct edge{
        int to,next;
        edge(){}
        edge(const int &_to,const int &_next){ to=_to,next=_next; }
    }e[maxm];
    int head[maxn],k;
    inline void init(){ memset(head,-,sizeof head); }
    inline void add(const int &u,const int &v){
        e[k]=edge(v,head[u]),head[u]=k++;
    }
}a,b,c,d;

inline int read(){
    register int x(); register char c(getchar());
    while(c<''||''<c) c=getchar();
    while(''<=c&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x;
}

int bel[maxn],val[maxn],semi[maxn],idom[maxn];
int fa[maxn],dfn[maxn],id[maxn],tot;
int n,m,size[maxn];

void dfs(int u){
    dfn[u]=++tot,id[tot]=u;
    for(register int i=a.head[u];~i;i=a.e[i].next){
        int v=a.e[i].to;
        if(!dfn[v]){
            fa[v]=u;
            dfs(v);
        }
    }
}

int find(int u){
    if(bel[u]==u) return u;
    int tmp=find(bel[u]);
    if(dfn[semi[val[bel[u]]]]<dfn[semi[val[u]]]) val[u]=val[bel[u]];
    return bel[u]=tmp;
}

inline void lengauer_tarjan(){
    int u,v;
    for(register int i=tot;i>;i--){
        u=id[i];
        for(register int i=b.head[u];~i;i=b.e[i].next){
            if(dfn[v=b.e[i].to]){
                find(v);//带权并查集维护最小边权
                if(dfn[semi[val[v]]]<dfn[semi[u]]) semi[u]=semi[val[v]];
            }
        }
        c.add(semi[u],u);
        bel[u]=fa[u],u=fa[u];
        for(register int i=c.head[u];~i;i=c.e[i].next){
            find(v=c.e[i].to);
            if(semi[val[v]]==u) idom[v]=u;
            else idom[v]=val[v];
        }//半必经点定理
    }
    for(register int i=;i<=tot;i++){
        u=id[i];
        if(idom[u]!=semi[u]) idom[u]=idom[idom[u]];
    }//必经点定理
}

void dfs_ans(int u){
    size[u]=;
    for(register int i=d.head[u];~i;i=d.e[i].next){
        int v=d.e[i].to;
        dfs_ans(v);
        size[u]+=size[v];
    }
}

int main(){
    a.init(),b.init(),c.init(),d.init();
    n=read(),m=read();
    for(register int i=;i<=m;i++){
        int u=read(),v=read();
        a.add(u,v),b.add(v,u);
    }
    dfs();

    for(register int i=;i<=n;i++) bel[i]=val[i]=semi[i]=i;
    lengauer_tarjan();
    for(int i=;i<=n;i++) d.add(idom[i],i);
    dfs_ans();
    for(register int i=;i<=n;i++) printf("%d ",size[i]);puts("");
    return ;
}

　　等厉害一点了再回来写证明......(逃)