OO第一单元总结分析

综述：本模块的内容为表达式求导，目的是通过不同项的嵌套四则运算求导这一基本思路熟悉面向对象的继承与接口机制。

一、三次作业总结分析

1.第一次作业：

1.1 作业分析

盼望着，盼望着，鸽了一年的oo终于要掀开它神秘的面纱了（高工狗的怨念）。第一次作业的要求是初级的表达式求导，这次作业中项和因子的概念没有加以区分，所以导致我并没有从中体会到oop的思想，加上当时还有托福考试于是第一次作业基本算是“混过去”了，只用一个简单的面向过程的模式进行了书写。第一次作业和以前面向过程不同的就是要处理各种各样的错误输入并进行判断，最后输出“WRONG FROMAT!”。在这次作业中实现了一个errorManipulate方法进行对不同错误输出的处理便于定位。

1.2 程序架构

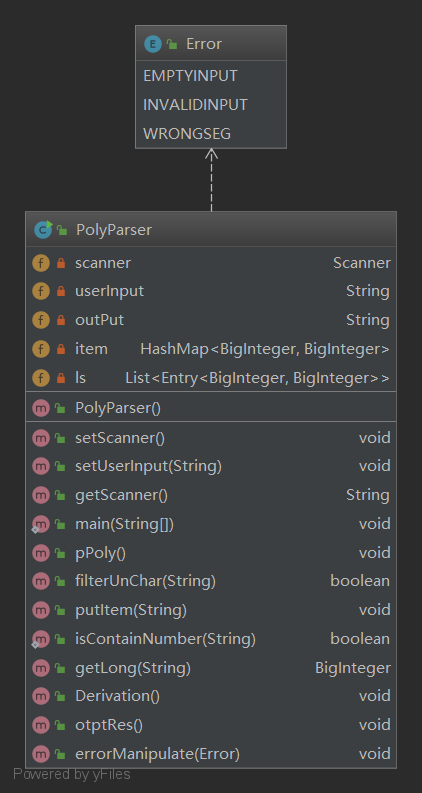
从图中可以看到笔者在第一次作业完全没有进行面向对象的抽象化过程，只是简单地按照 输入 -> 判断合法性并进行parse -> 记录项的系数以及指数 -> 进行求导 -> 输出 的按照方法进行分类的过程化流程，所以其兼容泛化性之低以及代码之丑也是可想而知了。

首先输入后会进行一系列的空格，\t和unchar的filter的预处理以简化后续的正则表达式处理部分，由于第一次作业的简单性，

正则表达式采用一整个字符串为正则的匹配方式。得到了每一项后分别记录每一项的系数和指数存入private变量itemRaw中，itemRaw以HashMap的形式进行存储。

求导只需按部就班地按照公式进行处理即可。

优化部分由于只是将同样的指数放在一起后进行系数的加减运算，所以也就和记录项的系数以及指数放在了一起。

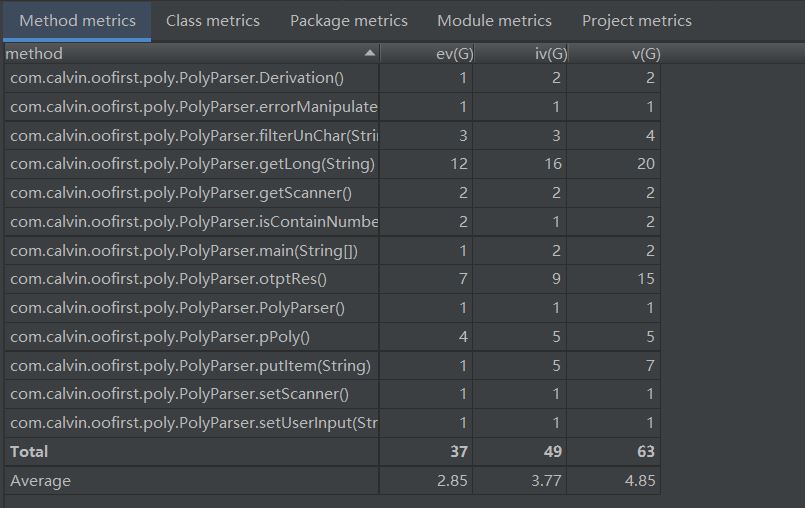
由于没有进行合理的需求分析，有些方法的复杂度由于嵌套if或者for的地方比较多造成了很大程度上的复杂度冗余

1.3 bug发现

在强测中发现了一个bug，经过查找发现是程序在复制（以后打死也不复制）的时候有一个正负号忘记更改，而这个错误产生的前提仅为--1*x并且省略-1的这种情况下，而且后续的自我测试没有对这个样例进行很好的覆盖，悔不当初。

1.4 总结

这次学到的东西主要就是正则表达式，虽然之前对正则表达式早有耳闻，不过这次还是第一次从头开始思考这则表达式的具体匹配问题。在debug过程中依照着讨论区大佬的指示，了解了正则表达式贪婪模式，非贪婪模式以及独占模式的区别，修改了自己正则爆栈的bug。同时了解了正则表达式的分组功能和反向引用功能，为后续开发打好基础。

2. 第二次作业

2.1 作业分析

第二次作业在第一次作业的基础上增加了因子的概念，即加入了乘法的计算，同时增加了三角函数这一个新的函数形式。从形式上来看这次作业的复杂度增加的地方主要在一个项内，即不同因子的重复出现以及组合。由于这次作业的优化部分和整个需求架构的方向不是特别一致，所以最终需要将优化部分抽离开来做。

2.2 程序架构

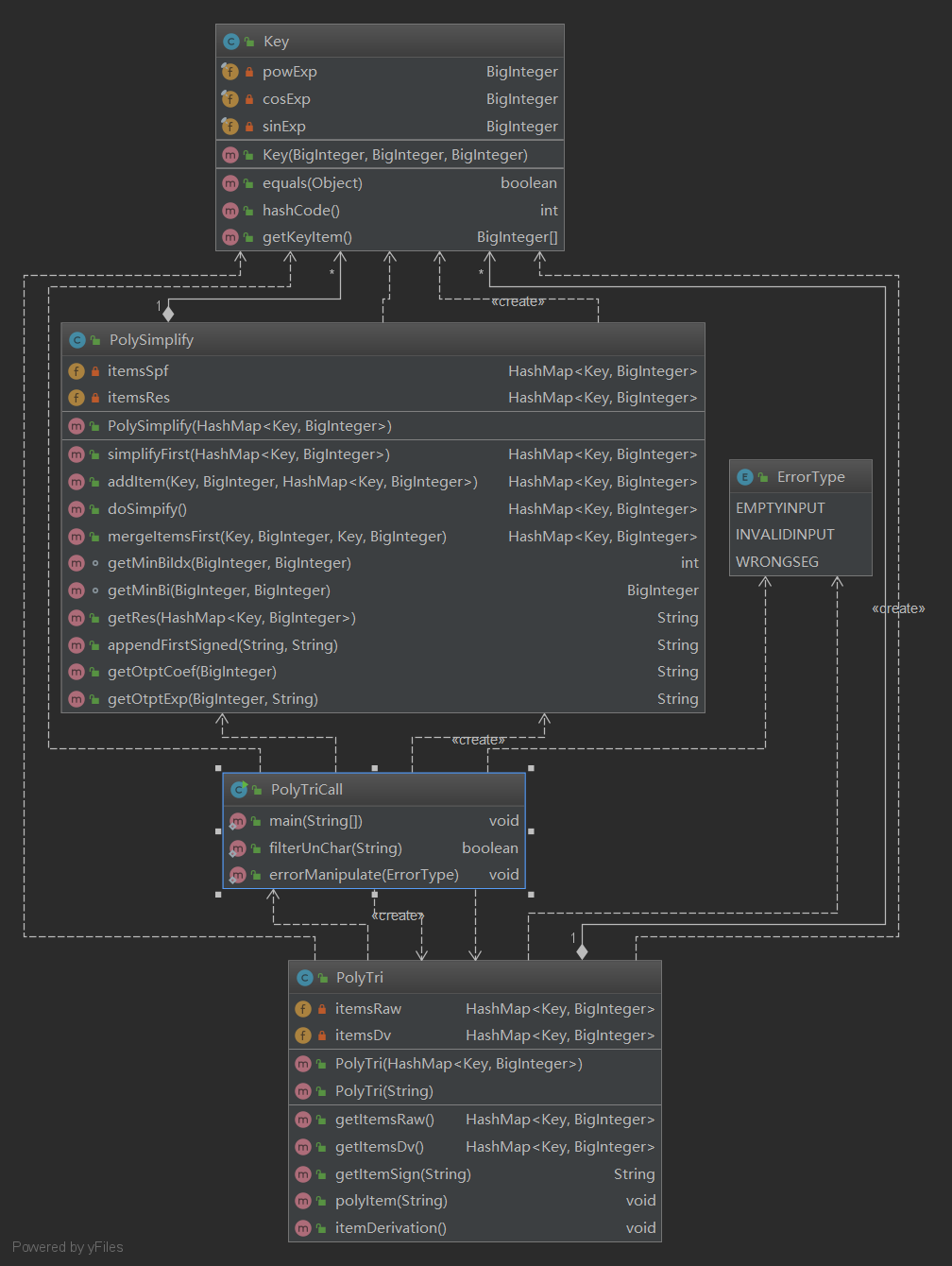
这次的作业采用了一个比较好想的处理方式：将每一项抽象为a*x^b*sin(x)^c*cos(x)^d （1），现在想来这种处理方式又是一个十分鸡肋的处理方式，因为它只能满足这种项内部因子的扩展，对嵌套的处理方式根本没有一丝帮助... 由于这种抽象方法这次我仍然没有领会到继承的精髓，因为在当时的我看来，每一个项都可以作为一个独立的数据结构，然后再进行数据之间的交互就好了，所以并没有区分不同项和因子之间的类型差异，只是以项为单位进行批量求导，化简操作，这也造成了第三次作业 叒全盘推到重建，浪费了大把时间。

这次的代码参考了部分第一次上机的代码，程序首先在PolyTriCall中进行字符串预处理，然后进入PolyTri的构造函数中进行parse，最终将parse好的（1）中结构（即为对应系数）存入HashMap中，键值对为<三个幂次->系数>。

这种新型的HashMap经过指导书的提示后我实现了一个新型的key类型供HashMap使用，书写时参考了Effective Java里面的规则 -- 两个equal的实力要拥有相同的HashCode，两个不同的实例尽量拥有不同的hashcode，以提高散列表的查找效率。

接下来的部分是求导，由于本次作业进行抽象之后求导仍旧是在一个项内的，不涉及项与项之间的关系，所以求导部分没有进行单独的类实现，而是直接写进了PolyTri的一个方法中（对对象的生疏让我能不用就不用，，这种坏习惯一定要改！！），通过getItemsRaw和getItemsDv方法可以分别获取求导之前以及求导之后的多项式项。

化简部分由于时间原因，只做了sin^2(x)+cos^2(x)=1的化简，化简时的思路比较混乱，以至于写的时候有一种拆东墙补西墙的感觉，而且在化简的时候就出现了类型对象取的少的尴尬之处了。比如对不同类型的factor做取exp的时候，我无法将这个方法做成接口或者继承的形式放在powfactor，sinfactor以及cosfactor这三者的类型中，有些取对象的方法就直接内嵌在了求导（例如merge）里面，给代码的可读性造成极大的影响，现在从头再看第二次作业的感觉就是做的时候有面向对象的心，可是写着写着就写回了原形。

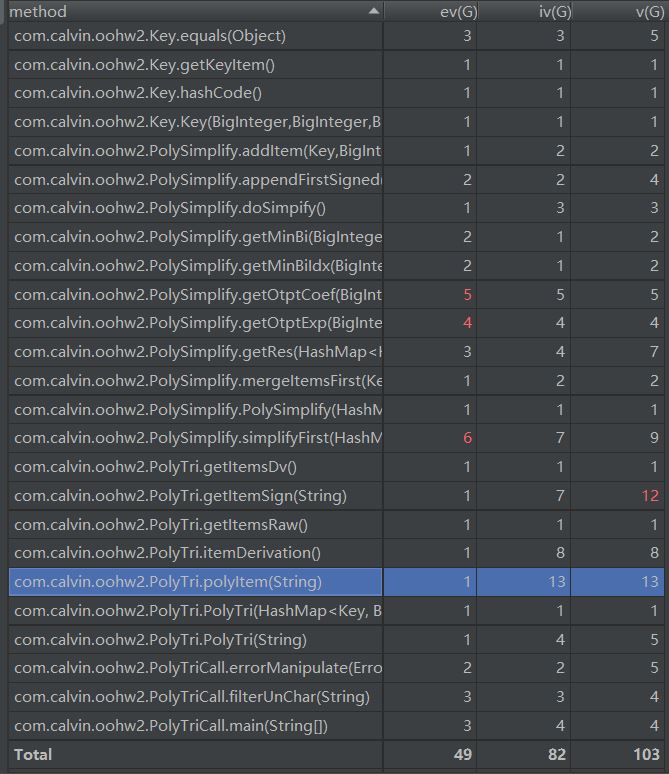
可以看到simplifyfirst这个方法里面有多次迭代以及循环，分支判断，导致其结构化很差，其余的两个也是由于分支判断的情况没有细分到各个factor中导致十分冗杂

2.3 bug发现

这部分在中测以及强测中均未发现bug

2.4 总结

虽然第二次作业没有什么bug，但是我在写完后仍然对自己没有掌握面向对象的思想而懊悔。这使得我在debug的时候经常发现很多莫名其妙的bug，想追根溯源却又变得十分困难。同时这次写的程序仍然是就题论题而毫无扩展性，在开始写第三次作业时这种感觉尤为强烈，希望自己可以引以为戒。

3.第三次作业

3.1 作业分析

第三次作业是“果不其然”的函数嵌套求导，即支持因子内部嵌套因子。由于表达式因子的存在这也就可以说是标准的表达式嵌套了。这次的作业对于我这种之前架构很差的人的要求就是能够编写出一个可以扩展的而且保持准确的架构模型。通过这一次的作业我终于了解到面向对象的魅力所在。

3.2 程序架构

这次的架构虽然看似很复杂，但是分解开来是十分清晰的。这次面对如此复杂的输入，我在思考了半天正则后发现没有什么思路能实现一个比较好的递归正则，于是将编译的思想应用到这次的parser中，因为毕竟编译器的lexer就是一个NFA自动机，它可以完全转化为一个正则表达式。后来有同学提醒可以通过项内因子来确定正则递归的结束条件，但是也没有改变这个架构。lexer的文法是：

在经过输入简单处理和lexer后，程序进入了parser来进行不同语法项的切分。切分的粒度就是文法左侧的非终结符。在写这部分的时候自己有些随意，但是自己在这里第一次写的时候有些小看神出鬼没的正负号导致后续debug有些摸不着头脑...anyway这是后话了。在进行了上述操作后，我没有直接进行各个项，各个因子的建立，而是维护了一个语法树，把各个项以加号相连，各个因子以乘号相连，嵌套结构以nested显示，叶子节点为各类factor，以下为2 * sin(cos((x^2+5)))^2 + 0 的语法树例子：

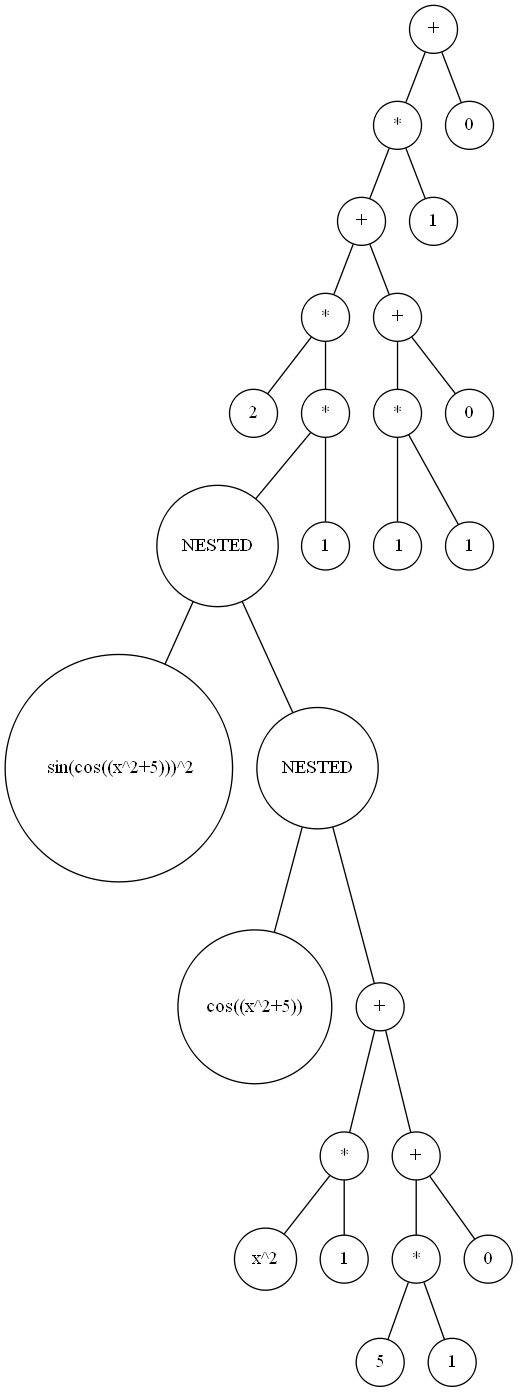
建立好语法树之后就是通过从上到下的递归来建立各个项的关系，这里需要采用后序遍历的方法，这样每次建立好子节点之后再去建立父结点，便于项的生成。

之后就在建立的表达式关系下从上至下跑一遍求导，求导使用接口实现的每次每部分求完导之后向上返回这部分的导数用于拼接。

3.3 bug发现

这次的bug都集中在强测阶段，这次的bug竟然是我最后临提交时因为修改一个临时发现的bug产生的，，，最后再修改bug的时候只是考虑到了括号较少的情况，没有想起来括号内嵌套多个的时候临时加一个负号会影响很多项，或者说是当时自己认为之前处理因子的时候在multiply的最外面加了括号可惜结果并没有，，，这次的bug一定程度上说明了bug与bug之间的耦合性，在修改bug的时候一定要建立在对自己的架构以及程序的细枝末节了解清楚的情况下，否则每修改一次bug就要进行一次工程化验证！

3.4 总结

这一部分算是让我真正体会到了一个oop程序的多态性是如何体现的。但是遗憾的是我的前期准备工作做得还是不充分，比如在词法分析的时候对表达式的括号问题界定不清，导致出现表达式级别仍会parse括号导致在factor中parse括号时判错，+ - 是否连空格问题没有预先处理导致parse时判断经常搞错，这些东西现在想一下都是一些架构时思考不到位的问题。还有表达式树这一步的建立其实单就这次作业来看是有些冗余的，完全可以按照从上到下的想法从输入式中取出各个项直接建立式子之间的关系。同时我还认识到了java语言浅拷贝与深拷贝的区别，因为我在表达式树的建立过程中进行了摘链挂链以及结点的销毁，在某处A的孩子结点B的挂到了另一个结点下面，如果销毁A的孩子结点，B也会跟着销毁，这种浅拷贝也让我在debug时吃了不少亏，下次再进行等号操作时一定要慎重！

二. 总结

在这第一部分的java面向对象课程中，我从一个java小白进化到一个对继承与多态有初步认识的新手。这一阶段的课程还算是比较中规中矩的，希望在接下来的多线程历练中我还能继续磨练自己的技能，在昆仑课程中前行！