Houdini SDF/Raymarching/等高曲面绘制

1 , SDF

<1> union  min(a,b)

<2> intersect: max(a,b)

<3> Substract  a-b  :

if(b> -a){

return b;

}

return -a;

2, 2d Plane SDF:

float planeSDF(float x;float y;float px;float py; float nx; float ny)
{
    return (x - px ) * nx + (y-py) *ny;
}

// box ramp to 0-1
vector min;
vector max;
getbbox(,min,max);
vector rpos = fit(@P, min ,max , set(,,) , set(,,) );
rpos.y =  - rpos.y; 

@Cd = planeSDF(
rpos.x , rpos.y ,
0.0f, 0.5f,
0.0f ,1.0f);

X和Y SDF平面切换比较简单:

/* X SDF Plane   */
@Cd = planeSDF(
rpos.x , rpos.y ,
0.5f, 0.0f,
1.0f ,0.0f);

/* Y SDF Plane  */
@Cd = planeSDF(
rpos.x , rpos.y ,
0.0f, 0.5f,
0.0f ,1.0f);

Houdini渲染一个： Raymarching 2d

Qt Framework:

 2,极坐标2d

1,心:

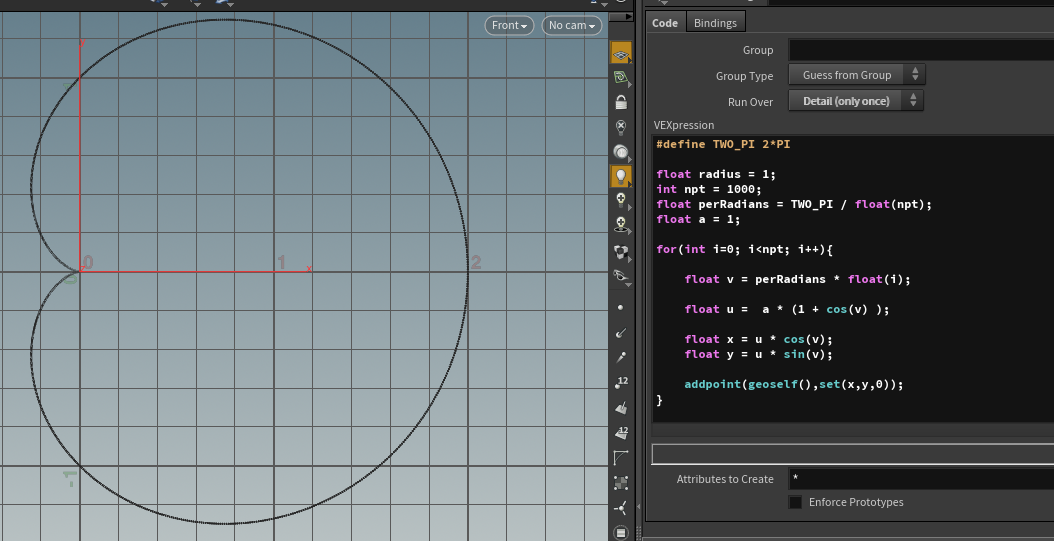
2:阿基米德螺线

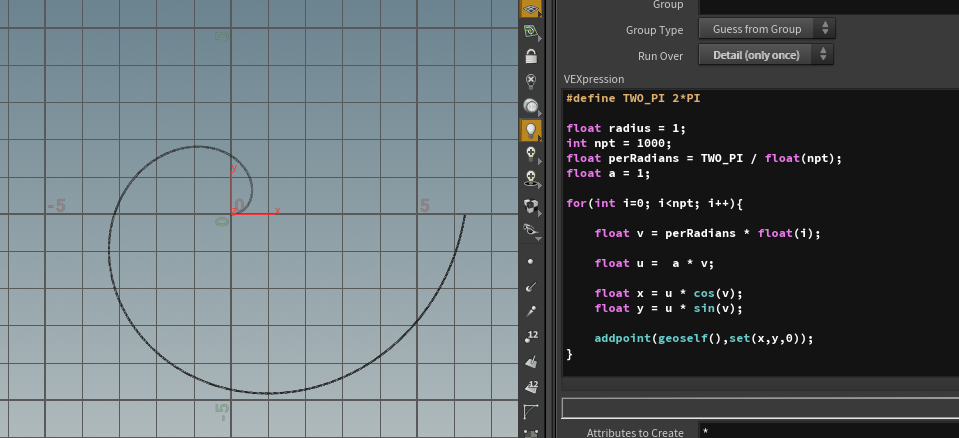
3,复数下的极坐标以及对图像产生的影响

这里的复数定义: Z = x + yi ;

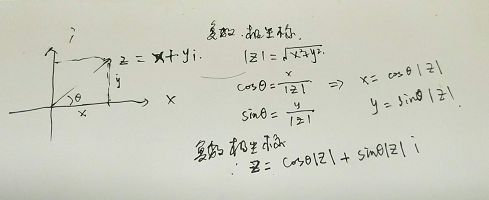
Houdini里扔一个图:

>> , z^2

float ex(float r; float theta)
{
    return cos(theta) * r;
}
float ey(float r; float theta)
{
    return sin(theta) * r;
}

// Z = x + yi;
// Z*Z = (x^2 - y^2) + (2xy)*i;

float real = @P.x* @P.x - @P.y*@P.y;
float img  =  * @P.x * @P.y;
float r = sqrt(real * real + img*img);
float theta = atan2(img,real);

@P.x = ex(r , theta);
@P.y = ey(r , theta);

>> Z -> -1/Z

float ex(float r; float theta)
{
    return cos(theta) * r;
}
float ey(float r; float theta)
{
    return sin(theta) * r;
}

// Z = x + yi;
// -1/z = -(x/(x^2+y^2)) + y/(x^2+y^2)i

float real = -(@P.x/(@P.x*@P.x + @P.y*@P.y)) ;
float img  = @P.y/(@P.x*@P.x + @P.y*@P.y) ;
float r = sqrt(real * real + img*img);
float theta = atan2(img,real);

@P.x = ex(r , theta);
@P.y = ey(r , theta);

e^z

Houdini如何画参数方程:

比如:r(t) = (1/t) i + sin(t) j

由于t 不能等于0:

float rmp = float(@ptnum) / float(@numpt-) + 0.000001;
rmp = rmp*;
@P.x = 1.0/rmp;
@P.y = sin(rmp);

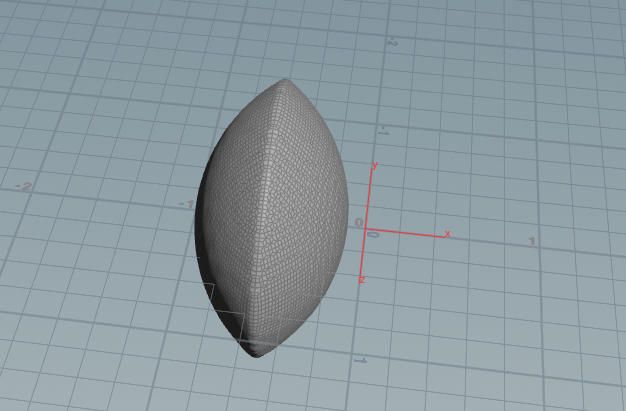
 Houdini ISO Surface:画等高面的利器：

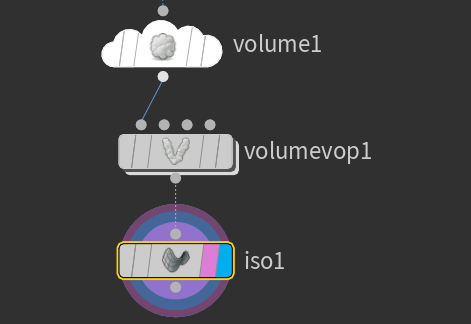
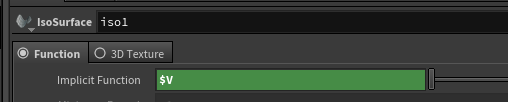
使用输入的值，volumevop里随便创建了半径为r = 0.4的SDF球:

则形成的iossurface是:

implicit function for isosurface: Houdini默认给的这个。这个是个半径为1的球。 这其实是一个 三元函数的一个等高面.

$X*$X + $Y*$Y + $Z*$Z - 

半径为5的圆柱则是: x^2 + y^2 = 5 (注意些Houdini由于y是向上，y和z要调换顺序)

$X*$X + $Z*$Z -

x^2+y^2 = z (注意些Houdini由于y是向上，y和z要调换顺序)

$X*$X + $Z*$Z -$Y

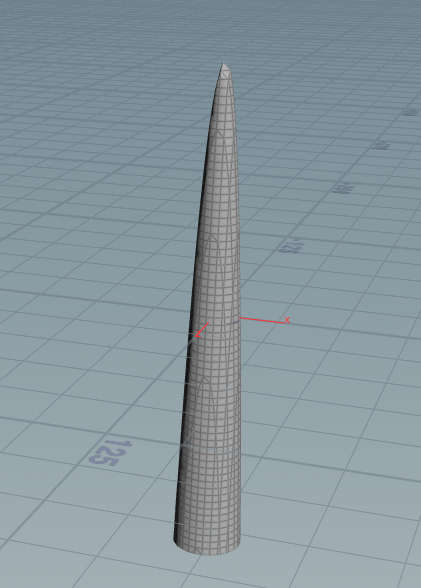
如果f(x,y) = 100 - x^2 - y^2

虽说是f(x,y)二元函数,但由于x,y ->对应一个z,画出来是个R^3空间的 三维曲面 ，所以f(x,y) = Z,

在houdini里要写 :

 - $X*$X - $Z*$Z - $Y

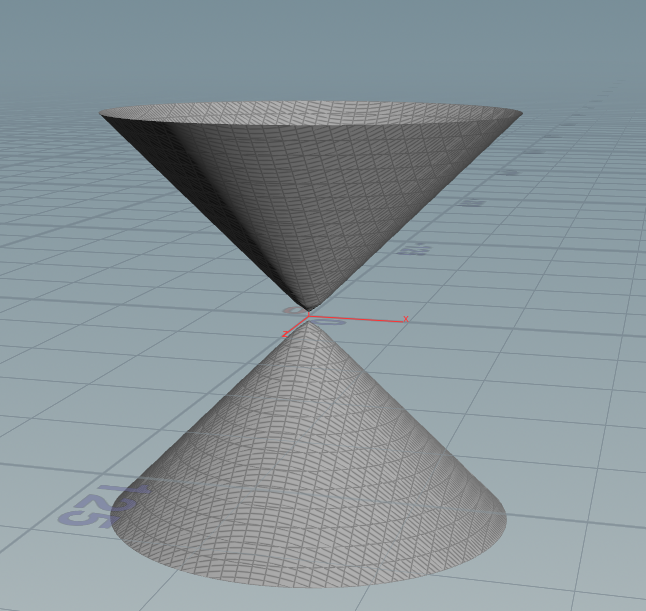
画双曲面:

z^2 - x^2 - y^2 = 1(注意些Houdini由于y是向上，y和z要调换顺序)

$Y*$Y - $X*$X - $Z*$Z - 

|x| + |y| 的等高线:

float grad = (abs(@P.x) + abs(@P.z));
@Cd = grad % ;

pow()之后：

float grad = (abs(@P.x) + abs(@P.z));
@Cd = pow(grad,) % ;

参考:

1,高等数学(同济大学)，托马斯微积分

2,https://zhuanlan.zhihu.com/milocode

3,https://www.youtube.com/watch?v=MRuhHGYUJSI