Kasaraju算法--强连通图遍历及其python实现

在理解有向图和强连通分量前必须理解与其对应的两个概念，连通图（无向图）和连通分量。

连通图的定义是：如果一个图中的任何一个节点可以到达其他节点，那么它就是连通的。

例如以下图形：

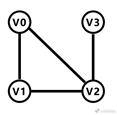
这是最简单的一个连通图，即使它并不闭合。由于节点间的路径是没有方向的，符合从任意一个节点出发，都可以到达其他剩余的节点这一条件，那么它就是连通图了。

连通分量

显然这也是一个图，只不过是由三个子图组成而已，但这并非一个连通图。这三个子图叫做这个图的连通分量，连通分量的内部归根还是一个连通图。

有向图：

在连通图的基础上增加了方向，两个节点之间的路径只能有单一的方向，即要么从节点A连向节点B，要么从节点B连向节点A。有向图与连通图（更准确来说是无向图）最大的区别在于节点之间的路径是否有方向。

有向图也分两种，一种是有环路的有向图。另外一种是无环路的有向图，即通常所说的有向无环图DAG（Directed Acyclic Graph）。严格来说，第一种有环路的图，如果任意一个节点都可以与其他节点形成环路，那么它也是一个连通图。

例如下面的就为一个有向图同时也是连通图：

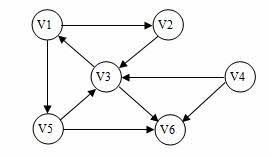
强连通分量

强连通分量SCCs（strongly connected components）是一种有向的连通图。

如果一个图的连通分量是它里面所有节点到能够彼此到达的最大子图，那么强连通分量SCCs就是一个有向图中所有节点能够彼此到达的子图。

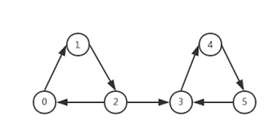
显然由345组成的子图是无法到达由012组成的子图的。那么012和345分别组成两个强连通分量。

在实际的现实问题中，我们考虑问题可能就不会简单地研究无向图。例如地图上的最短路径规划，ARP路由算法等等，考虑的都是有向图的问题。

如果有这样一个需求，我们希望用最少的次数遍历所有节点，怎么处理呢？

时间效应问题，强连通分量间的时间问题。

如果有向图的各个强连通分量中的元素个数相仿，那么，它们内部分别进行遍历的时间量级别是相等的，但实际情况是，这种情况很少发生。一般从一个强连通分量到另一个强连通分量。

正如上面的需求：如何用最少的次数遍历整个有向图的所有节点。假设我们将0、1、2组成子图1，将3、4、5组成子图，子图1有一条指向子图2的路径。这时候，我们从子图1的任意一点开始遍历。假设我们从1开始遍历，那么遍历的顺序将会是1—2，那么来到2的时候问题来了，是先走0的路径还是走子图1和子图2之间的路径去遍历节点3呢？

如果我们先遍历节点0，那么我们遍历完节点0之后，发现节点1已经遍历过，就会返回节点2，再沿着子图1和子图2之间的路径去遍历子图2。这看起来是挺合理的。

但问题是，如果是先遍历节点3（也就是说先遍历子图2）呢？

假设沿着子图1和子图2的路径去遍历子图2，那么子图2遍历完后，子图1还剩下节点0没有被遍历，这时候就会出现很为难的事情，因为之前遍历的情况无法判断哪些节点是没有遍历的，只能是原路返回，依次去从新遍历，“发现”哪些节点是还没去遍历的。似乎上图比较简单，这种方法不会耗费太多的时间。但如果是节点2连接着（并指向）许多个强连通子图的有向图，这种“返回式”的遍历将会是很费劲的一件事。

为了解决这个问题，Kosaraju算法提出了它的解决方案。Kosaraju算法的核心操作是将所有节点间的路径都翻转过来。下面分析一下为什么这种算法有它的优势。

还是拿上面的图来讲述。想象一下上面的有向图中的所有节点间的路径都翻转过来了。读者可以自己用一张纸简单画一下。就像下面的图：

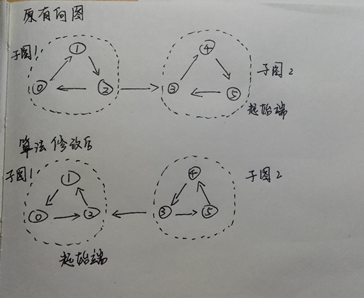
这一次，我们还是以0、1、2组成子图1，以3、4、5组成子图2。所不同的是，这次遍历的起始点从子图1开始。

多强连通分量的有向图

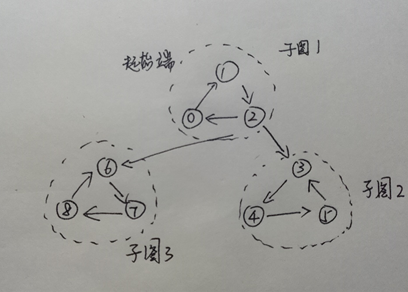
再来看一下这个多子图的强连通图，如果像上图所示，从子图1开始，就会像上文提到的那样，遍历到节点2，会出现多个去向的问题。而在还没有遍历完子图1的前提下，从节点2过渡到子图2/子图3，再回溯的时候会引来较大的麻烦。通过Kosaraju算法之后，从2节点出发的路径都会变成指向2。此时，遍历的起点还是从子图1开始，由于子图1没有出路，就不会出现上面所说的问题。再遍历完子图1后，继续遍历子图2、子图3。而子图2、子图3的遍历都是在强连通分量内部实现的。

算法实现

邻接集表示的有向图

N={
    "a":{"b"},   #a
    "b":{"c"},   #b
    "c":{"a","d","g"},   #c
    "d":{"e"},   #d
    "e":{"f"},   #e
    "f":{"d"},   #f
    "g":{"h"},   #g
    "h":{"i"},   #h
    "i":{"g"}    #i
}

翻转图实现代码：

def re_tr(G):
    GT = {}
    for u in G:
        for v in G[u]:
            # print(GT)
            if GT.get(v):
                GT[v].add(u)
            else:
                GT[v] = set()
                GT[v].add(u)

    return GT

深度遍历算法实现代码：

#递归实现深度优先排序
def rec_dfs(G,s,S=None):
    if S is None:
        #S = set()    #集合存储已经遍历过的节点
        S = list()    #用列表可以更方便查看遍历的次序，而用集合可以方便用difference求差集
    # S.add(s)
    S.append(s)
    print(S)
    for u in G[s]:
        if u in S:continue
        rec_dfs(G,u,S)

return S

在强连通图内遍历

#遍历有向图的强连通分量
def walk(G,start,S=set()):     #传入的参数S，即上面的seen很关键，这避免了通过连通图之间的路径进行遍历
    P,Q = dict(),set()      #list存放遍历顺序，set存放已经遍历过的节点
    P[start] = None
    Q.add(start)
    while Q:
        u = Q.pop()                      #选择下一个遍历节点（随机性）
        for v in G[u].difference(P,S):         #返回差集
            Q.add(v)
            P[v] = u
    print(P)
    return P

获得强连通分量

#获得各个强连通图
def scc(G):
    GT = re_tr(G)
    sccs,seen = [],set()
    for u in rec_dfs(G,"a"):    #以a为起点
        if u in seen:continue
        C = walk(GT,u,seen)
        seen.update(C)
        sccs.append(C)
    return sccs

单元测试

print(scc(N))

结果：
{'a': None, 'c': 'a', 'b': 'c'}
{'d': None, 'f': 'd', 'e': 'f'}
{'g': None, 'i': 'g', 'h': 'i'}
[{'a': None, 'c': 'a', 'b': 'c'}, {'d': None, 'f': 'd', 'e': 'f'}, {'g': None, 'i': 'g', 'h': 'i'}]

这是本人学习过程所写的第一篇关于图的算法文章，供大家一起学习讨论。其中难免会有错误。如有错误之处，请各位指出，万分感谢！