IEEE Trans 2009 Stagewise Weak Gradient Pursuits论文学习

论文在第二部分先提出了贪婪算法框架，如下截图所示：

接着根据原子选择的方法不同，提出了SWOMP（分段弱正交匹配追踪）算法，以下部分为转载《压缩感知重构算法之分段弱正交匹配追踪(SWOMP)》

分段弱正交匹配追踪(StagewiseWeak OMP)可以说是StOMP的一种改进算法，它们的唯一不同是选择原子时的门限设置，这可以降低对测量矩阵的要求。我们称这里的原子选择方式为“弱选择”（Weak Selection），详见文献[1]的第3部分“III. STAGEWISE WEAK ELEMENTSELECTION”。

1 SWOMP重构算法流程

2 分段弱正交匹配追踪(SWOMP)Matlab代码(CS_SWOMP.m)

代码基本与StOMP.m一致，不同之处只是修改了门限，为了测试α=1时的重构效果，门限比较时由StOMP的大于改为了大于等于。

function [ theta ] = CS_SWOMP( y,A,S,alpha )
%CS_SWOMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-05-11
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%   y = Phi*Psi * theta
%   令 A = Phi*Psi, 则y=A*theta
%   S is the maximum number of SWOMP iterations to perform
%   alpha is the threshold parameter
%   现在已知y和A，求theta
%   Reference:Thomas Blumensath，Mike E. Davies．Stagewise weak gradient
%   pursuits[J]．IEEE Transactions on Signal Processing，2009，57(11)：4333-4346．
    if nargin < 4
        alpha = 0.5;%alpha范围(0,1),默认值为0.5
    end
    if nargin < 3
        S = 10;%S默认值为10
    end
    [y_rows,y_columns] = size(y);
    if y_rows<y_columns
        y = y';%y should be a column vector
    end
    [M,N] = size(A);%传感矩阵A为M*N矩阵
    theta = zeros(N,1);%用来存储恢复的theta(列向量)
    Pos_theta = [];%用来迭代过程中存储A被选择的列序号
    r_n = y;%初始化残差(residual)为y
    for ss=1:S%最多迭代S次
        product = A'*r_n;%传感矩阵A各列与残差的内积
        sigma = max(abs(product));
        Js = find(abs(product)>=alpha*sigma);%选出大于阈值的列
        Is = union(Pos_theta,Js);%Pos_theta与Js并集
        if length(Pos_theta) == length(Is)
            if ss==1
                theta_ls = 0;%防止第1次就跳出导致theta_ls无定义
            end
            break;%如果没有新的列被选中则跳出循环
        end
        %At的行数要大于列数，此为最小二乘的基础(列线性无关)
        if length(Is)<=M
            Pos_theta = Is;%更新列序号集合
            At = A(:,Pos_theta);%将A的这几列组成矩阵At
        else%At的列数大于行数，列必为线性相关的,At'*At将不可逆
            if ss==1
                theta_ls = 0;%防止第1次就跳出导致theta_ls无定义
            end
            break;%跳出for循环
        end
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
        %At*theta_ls是y在At列空间上的正交投影
        r_n = y - At*theta_ls;%更新残差
        if norm(r_n)<1e-6%Repeat the steps until r=0
            break;%跳出for循环
        end
    end
    theta(Pos_theta)=theta_ls;%恢复出的theta
end

3 SWOMP单次重构测试代码

以下测试代码基本与OMP单次重构测试代码一样。代码中“Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵”并不像StOMP一样要求一定要除以sqrt(M)，这也是SWOMP对StOMP的最大改进之处。

%压缩感知重构算法测试
clear all;close all;clc;
M = 128;%观测值个数
N = 256;%信号x的长度
K = 30;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的，且位置是随机的
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y
%% 恢复重构信号x
tic
theta = CS_SWOMP( y,A);
x_r = Psi * theta;% x=Psi * theta
toc
%% 绘图
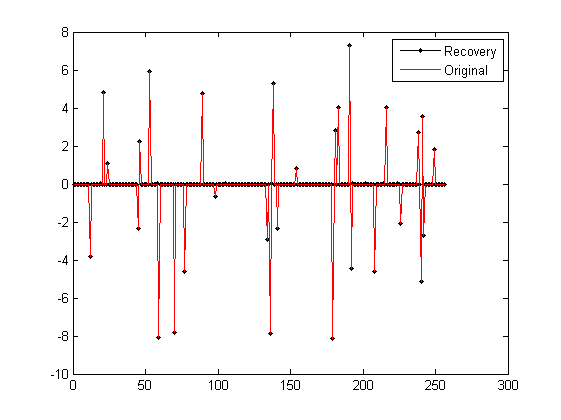
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

运行结果如下：（信号为随机生成，所以每次结果均不一样）

1）图：

 2）Command  windows

        Elapsedtime is 0.093673 seconds.

        恢复残差：

        ans=

          2.9037e-014

4 门限参数α、测量数M与重构成功概率关系曲线绘制例程代码

因为文献[1]中对门限参数α给出的是一个取值范围，所以有必要仿真α取不同值时的重构效果。以下的代码是基于StOMP相应的测试代码修改的，基本结构一样，只是α的测试值共10个，而在StOMP中ts的测试值共6个。

%压缩感知重构算法测试
clear all;close all;clc;
M = 128;%观测值个数
N = 256;%信号x的长度
K = 30;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的，且位置是随机的
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵  clear all;close all;clc;
%% 参数配置初始化
CNT = 1000;%对于每组(K,M,N)，重复迭代次数
N = 256;%信号x的长度
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
alpha_set = 0.1:0.1:1;
K_set = [4,12,20,28,36];%信号x的稀疏度集合
Percentage = zeros(N,length(K_set),length(alpha_set));%存储恢复成功概率
%% 主循环，遍历每组(alpha,K,M,N)
tic
for tt = 1:length(alpha_set)
    alpha = alpha_set(tt);
    for kk = 1:length(K_set)
        K = K_set(kk);%本次稀疏度
        %M没必要全部遍历，每隔5测试一个就可以了
        M_set=2*K:5:N;
        PercentageK = zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
        for mm = 1:length(M_set)
           M = M_set(mm);%本次观测值个数
           fprintf('alpha=%f,K=%d,M=%d\n',alpha,K,M);
           P = 0;
           for cnt = 1:CNT %每个观测值个数均运行CNT次
                Index_K = randperm(N);
                x = zeros(N,1);
                x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的，且位置是随机的
                Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
                A = Phi * Psi;%传感矩阵
                y = Phi * x;%得到观测向量y
                theta = CS_SWOMP(y,A,10,alpha);%恢复重构信号theta
                x_r = Psi * theta;% x=Psi * theta
                if norm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
                    P = P + 1;
                end
           end
           PercentageK(mm) = P/CNT*100;%计算恢复概率
        end
        Percentage(1:length(M_set),kk,tt) = PercentageK;
    end
end
toc
save SWOMPMtoPercentage1000 %运行一次不容易，把变量全部存储下来
%% 绘图
for tt = 1:length(alpha_set)
    S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
    figure;
    for kk = 1:length(K_set)
        K = K_set(kk);
        M_set=2*K:5:N;
        L_Mset = length(M_set);
        plot(M_set,Percentage(1:L_Mset,kk,tt),S(kk,:));%绘出x的恢复信号
        hold on;
    end
    hold off;
    xlim([0 256]);
    legend('K=4','K=12','K=20','K=28','K=36');
    xlabel('Number of measurements(M)');
    ylabel('Percentage recovered');
    title(['Percentage of input signals recovered correctly(N=256,alpha=',...
        num2str(alpha_set(tt)),')(Gaussian)']);
end
for kk = 1:length(K_set)
    K = K_set(kk);
    M_set=2*K:5:N;
    L_Mset = length(M_set);
    S = ['-ks';'-ko';'-kd';'-k*';'-k+';'-kx';'-kv';'-k^';'-k<';'-k>'];
    figure;
    for tt = 1:length(alpha_set)
        plot(M_set,Percentage(1:L_Mset,kk,tt),S(tt,:));%绘出x的恢复信号
        hold on;
    end
    hold off;
    xlim([0 256]);
    legend('alpha=0.1','alpha=0.2','alpha=0.3','alpha=0.4','alpha=0.5',...
        'alpha=0.6','alpha=0.7','alpha=0.8','alpha=0.9','alpha=1.0');
    xlabel('Number of measurements(M)');
    ylabel('Percentage recovered');
    title(['Percentage of input signals recovered correctly(N=256,K=',...
        num2str(K),')(Gaussian)']);
end
y = Phi * x;%得到观测向量y
%% 恢复重构信号x
tic
theta = CS_SWOMP( y,A);
x_r = Psi * theta;% x=Psi * theta
toc
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

本程序在联想ThinkPadE430C笔记本（4GBDDR3内存，i5-3210）上运行共耗时8430.877154秒（时间较长，运行时可以干点别的事情了），程序中将所有数据均通过“save SWOMPMtoPercentage1000”存储了下来，以后可以再对数据进行分析，只需“load SWOMPMtoPercentage1000”即可。

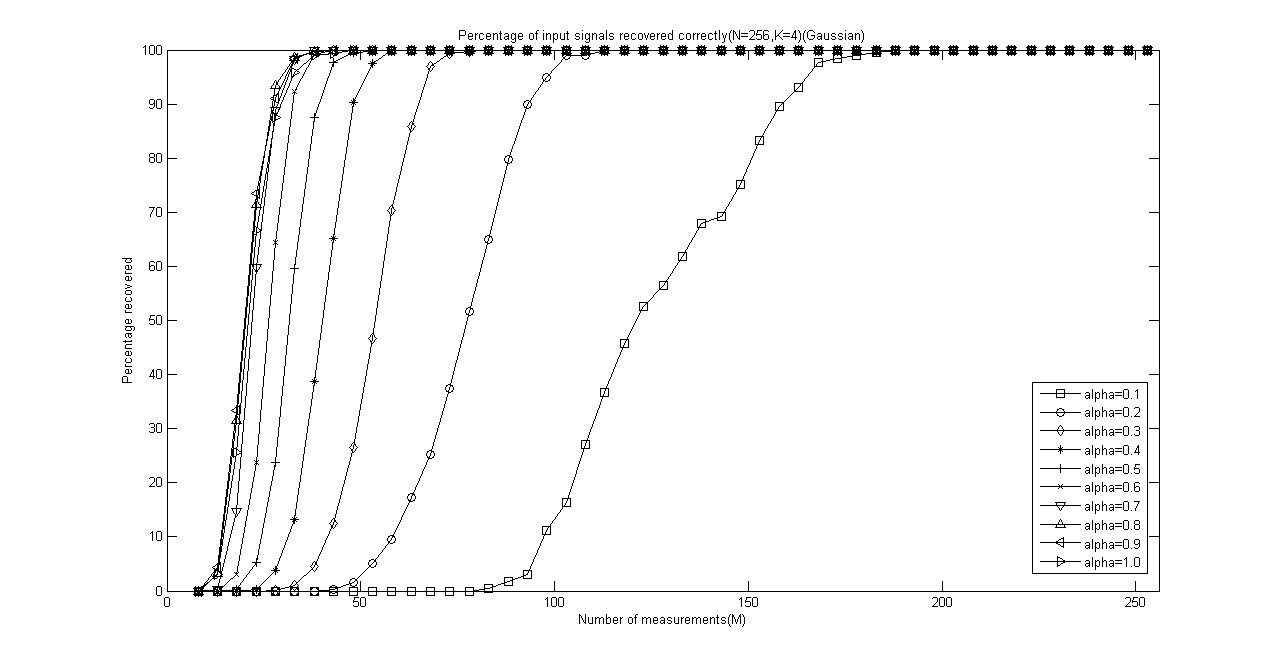
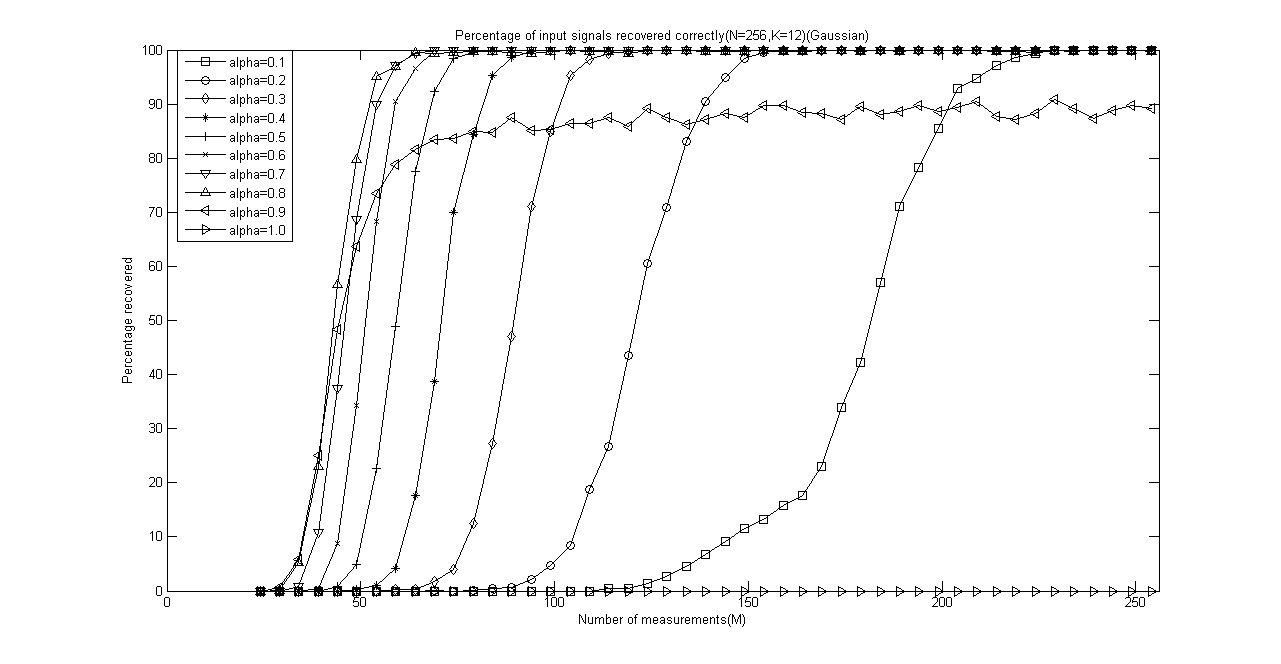
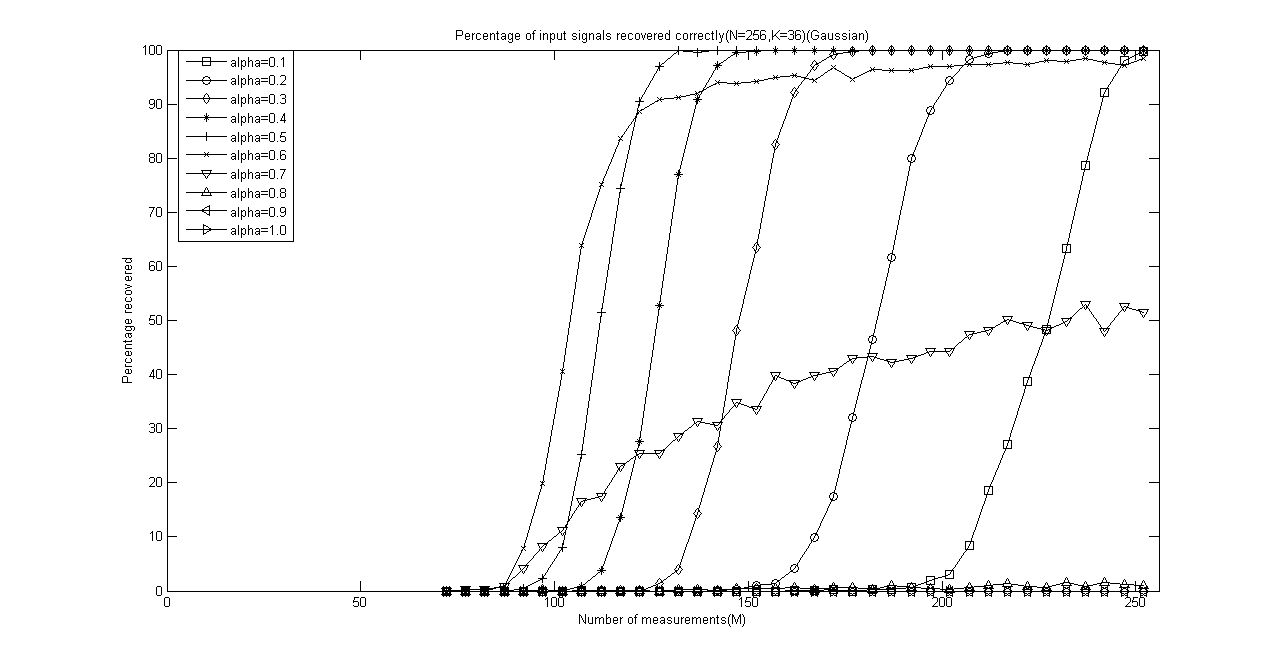
程序运行结束会出现10+5=11幅图，前10幅图分别是α分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1.0时的测量数M与重构成功概率关系曲线（类似于OMP此部分，这里只是对每一个不同的α画出一幅图），后5幅图是分别将稀疏度K为4、12、20、28、32时将十种α取值的测量数M与重构成功概率关系曲线绘制在一起以比较α对重构结果的影响。

以下是α分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和 1.0时的测量数M与重构成功概率关系曲线：

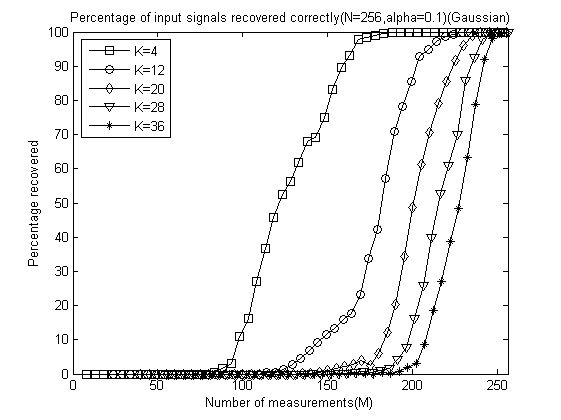
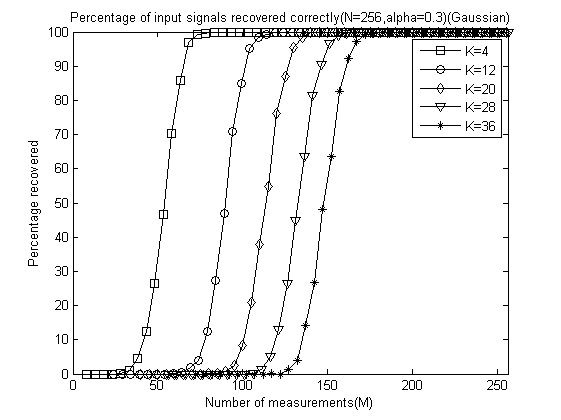
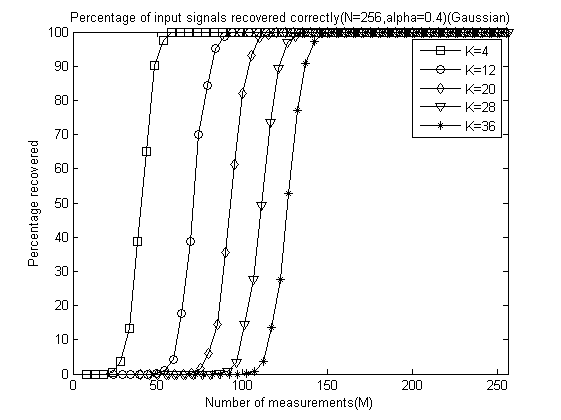
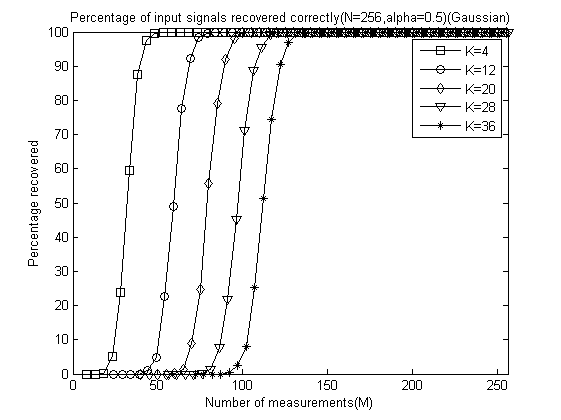
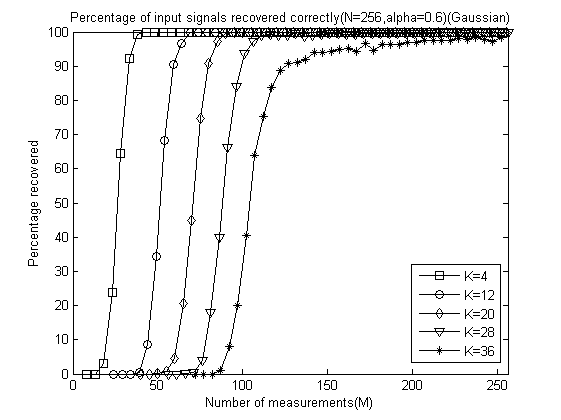
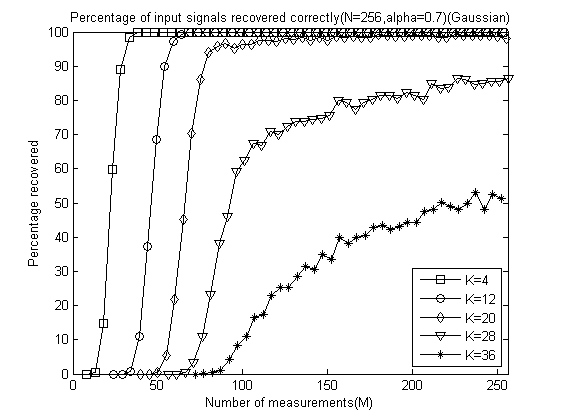
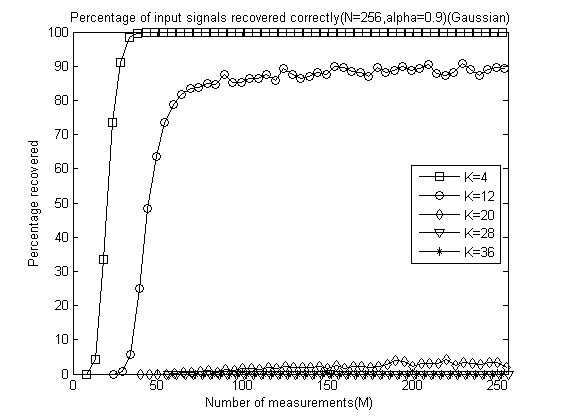
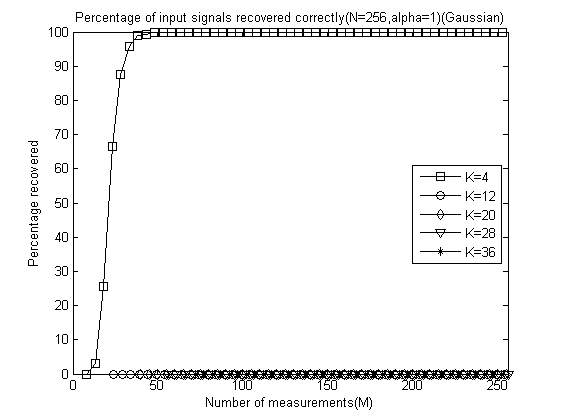
以下是稀疏度K为4、12、20、28、32时将十种α取值的测量数M与重构成功概率关系曲线放在一起的五幅图：