Spark 贝叶斯分类算法

　　一、贝叶斯定理数学基础

　　我们都知道条件概率的数学公式形式为

　　即B发生的条件下A发生的概率等于A和B同时发生的概率除以B发生的概率。

　　根据此公式变换，得到贝叶斯公式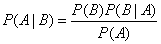：  即贝叶斯定律是关于随机事件A和B的条件概率（或边缘概率）的一则定律。通常，事件A在事件B发生的条件溪的概率，与事件B在事件A的条件下的概率是不一样的，而贝叶斯定律就是描述二者之间的关系的。

　　更进一步将贝叶斯公式进行推广，假设事件A发生的概率是由一系列的因素(A1,A2,A3,...An)决定的，则事件A的全概率公式为：

　　

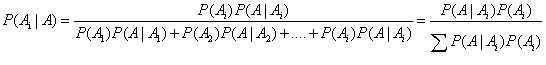
　　二、朴素贝叶斯分类

　　朴素贝叶斯分类是一种十分简单的分类算法，其思想基础是：对于给定的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项就属于哪个类别。

　　假设V=(v1,v2,v3....vn)是一个待分项，而vn为V的每个特征向量；

　　       B=(b1,b2,b3...bn)是一个分类集合，bn为每个具体的分类；

　　　　如果需要测试某个Vn归属于B集合中的哪个具体分类，则需要计算P(bn|V)，即在V发生的条件下，归属于b1,b2,b3,....bn中哪个可能性最大。即：

　　　　

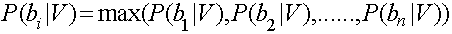
　　　　因此，这个问题转换成求每个待分项分配到集合中具体分类的概率是多少。而这个·具体概率的求法可以使用贝叶斯定律。

　　　　

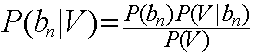
　　　　经过变换得出：

　　　　

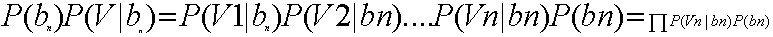
　　三、MLlib对应的API

　　1、贝叶斯分类伴生对象NativeBayes,原型：

object NaiveBayes extends scala.AnyRef with scala.Serializable {
  def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
  def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint], lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
}

　　其主要定义了训练贝叶斯分类模型的train方法，其中input为训练样本，lambda为平滑因子参数。

　　2、train方法，其是NativeBayes对象的静态方法，根据设置的朴素贝叶斯分类参数新建朴素贝叶斯分类类，并执行run方法进行训练。

　　3、朴素贝叶斯分类类NaiveBayes,原型：

class NaiveBayes private (private var lambda : scala.Double) extends scala.AnyRef with scala.Serializable with org.apache.spark.Logging {
  def this() = { /* compiled code */ }
  def setLambda(lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayes = { /* compiled code */ }
  def run(data : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
}

　　4、run方法，该方法主要计算先验概率和条件概率。首先对所有样本数据进行聚合，以label为key，聚合同一个label的特征features，得到所有label的统计(label，features之和),然后根据label统计数据，再计算p(i),和theta(i)(j)，最后，根据类别标签列表、类别先验概率、各类别下的每个特征的条件概率生成贝叶斯模型。

　　先验概率并取对数p(i)=log(p(yi))=log((i类别的次数+平滑因子)/(总次数+类别数*平滑因子)）)

　　各个特征属性的条件概率，并取对数

　　theta(i)(j)=log(p(ai|yi))=log(sumTermFreqs(j)+平滑因子)-thetaLogDenom

　　其中，theta(i)(j)是类别i下特征j的概率，sumTermFreqs(j)是特征j出现的次数，thetaLogDenom一般分2种情况，如下：

　　　　1.多项式模型

　　　　　　thetaLogDenom=log(sumTermFreqs.values.sum+ numFeatures* lambda)

　　　　　　其中，sumTermFreqs.values.sum类别i的总数，numFeatures特征数量，lambda平滑因子

　　　　2.伯努利模型

　　　　　　thetaLogDenom=log(n+2.0*lambda)

　　5、aggregated:对所有样本进行聚合统计，统计没个类别下的每个特征值之和及次数。

　　6、pi表示各类别·的·先验概率取自然对数的值

　　7、theta表示各个特征在各个类别中的条件概率值

　　8、predict:根据模型的先验概率、条件概率，计算样本属于每个类别的概率，取最大项作为样本的类别

　　9、贝叶斯分类模型NaiveBayesModel包含参数：类别标签列表(labels)、类别先验概率(pi)、各个特征在各个类别中的条件概率(theta)。

　　四、使用示例

　　1、样本数据:

0,1 0 0
0,2 0 0
1,0 1 0
1,0 2 0
2,0 0 1
2,0 0 2

　　

import org.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.{SparkConf, SparkContext}

object Bayes {
  def main(args: Array[String]): Unit = {
    val conf=new SparkConf().setAppName("BayesDemo").setMaster("local")
    val sc=new SparkContext(conf)
    //读取样本数据，此处使用自带的处理数据方式·
    val data=MLUtils.loadLabeledPoints(sc,"d://bayes.txt")
    //训练贝叶斯模型
    val model=NaiveBayes.train(data,1.0)
    //model.labels.foreach(println)
    //model.pi.foreach(println)
    val test=Vectors.dense(0,0,100)
    val res=model.predict(test)
    println(res)//输出结果为2.0
  }
}

　　

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.{SparkConf, SparkContext}

object Bayes {
  def main(args: Array[String]): Unit = {
    //创建spark对象
    val conf=new SparkConf().setAppName("BayesDemo").setMaster("local")
    val sc=new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)
    //读取样本数据
    val data=sc.textFile("d://bayes.txt")//读取数据
    val demo=data.map{ line=>//处理数据
      val parts=line.split(',')//分割数据·
      LabeledPoint(parts(0).toDouble,//标签数据转换
        Vectors.dense(parts(1).split(' ').map(_.toDouble)))//向量数据转换
    }
    //将样本数据分为训练样本和测试样本
    val sp=demo.randomSplit(Array(0.6,0.4),seed = 11L)//对数据进行分配
    val train=sp(0)//训练数据
    val testing=sp(1)//测试数据
    //建立贝叶斯分类模型，并进行训练
    val model=NaiveBayes.train(train,lambda = 1.0)

    //对测试样本进行测试
    val pre=testing.map(p=>(model.predict(p.features),p.label))//验证模型
    val prin=pre.take(20)
    println("prediction"+"\t"+"label")
    for(i<- 0 to prin.length-1){
      println(prin(i)._1+"\t"+prin(i)._2)
    }
　　　　val accuracy=1.0 *pre.filter(x=>x._1==x._2).count()//计算准确度

println(accuracy)

}
 }