有限等距性质RIP

/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/113cb19292fa4d61b5fc7ea4ef63bb1f/untitle.png)
(1) y为观测所得向量,大小为M×1
(2) x为原信号,大小为N×1
(3) θ为K稀疏的,是信号在x在某变换域的稀疏表示
(4) Φ称为观测矩阵、测量矩阵、测量基,大小为M×N
(5) Ψ称为变换矩阵、变换基、稀疏矩阵、稀疏基、正交基字典矩阵,大小为N×N
(6) A称为测度矩阵、传感矩阵、CS信息算子,大小为M×N
上式中,一般有K<<M<<N,后面三个矩阵各个文献的叫法不一,以后我将Φ称为测量矩阵、将Ψ称为稀疏矩阵、将A称为传感矩阵。
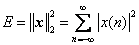
/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/3a7c45f60ab94c8681e26438027cde40/untitle.gif)
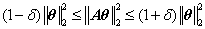
/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/7bcd88572dab4400a6115eac11ab02cf/untitle.gif) ||Aθ||2
||Aθ||2/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/3a619e09d3c94800a7e8f5064719f248/untitle.gif) 2实际上是||y||2
2实际上是||y||2/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/3a619e09d3c94800a7e8f5064719f248/untitle.gif) 2,即输出信号的能量, ||θ||2
2,即输出信号的能量, ||θ||2/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/3a619e09d3c94800a7e8f5064719f248/untitle.gif) 2
2/youdaoyun/Ynote/qq62B8CB8B9DB7E86B77B06F836EE1FF2E/ce30a104270e4f3b88c98a8c8f7825af/untitle.gif) 即输入信号的能量(稀疏变换x=Ψθ为正交变换,而正交变换保持能量不变,即信号理论中的Parseval定理)。
即输入信号的能量(稀疏变换x=Ψθ为正交变换,而正交变换保持能量不变,即信号理论中的Parseval定理)。
有限等距性质RIP的更多相关文章
- 浅谈压缩感知(十七):测量矩阵之有限等距常数RIC的计算
有限等距常数(RestrictedIsometry Constant, RIC)是与有限等距性质(Restricted IsometryProperty, RIP)紧密结合在一起的一个参数. 一.RI ...
- 压缩感知(CS)
总结一下最近看的压缩感知(Compressed Sensiong)的内容. 它是在采样过程中完成了数据压缩的过程. 一. 将模拟信号转换为计算机能够处理的数字信号,必然要经过采样的过程.问题在于,应该 ...
- 浅谈压缩感知(十六):感知矩阵之RIP
在压缩感知中,总是看到"矩阵满足RIP"之类的字眼,没错,这是一个压缩感知绕不开的术语,有限等距性质(Restricted Isometry Property, RIP). 注意: ...
- [中英双语] 数学缩写列表 (List of mathematical abbreviations)
List of mathematical abbreviations From Wikipedia, the free encyclopedia 数学缩写列表 维基百科,自由的百科全书 This ar ...
- 基于Hash算法的高维数据的最近邻检索
一.摘要 最紧邻检索:一种树基于树结构,一种是基于hash a.随机投影算法,需要产生很多哈希表,才能提高性能. b.基于学习的哈希算法在哈希编码较短时候性能不错,但是增加编码长度并不能显著提高性能. ...
- TCP/IP入门(2) --网络层
/** 本篇博客由 126(127不可用) 2^24 -2 B 2^14 -1 128.1 191.255 2^16 -2 C 2^21 -1 192.0.1 223.255.255 2^8 -2 D ...
- 动态选路、RIP协议&&OSPF协议详解
动态选路.RIP协议&&OSPF协议详解 概念 当相邻路由器之间进行通信,以告知对方每个路由器当前所连接的网络,这时就出现了动态选路.路由器之间必须采用选路协议进行通信,这样的选路协议 ...
- TCP/IP笔记 二.网络层(2)——ICMP,RIP,OSPF,BGP
1. ICMP ICMP (Internet Control Message Protocol) 作用:提高 IP 数据报交付成功的机会. 1.1 特点 ICMP 允许主机或路由器报告差错情况和提供有 ...
- 一类SG函数递推性质的深入分析——2018ACM陕西邀请赛H题
题目描述 定义一种有根二叉树\(T(n)\)如下: (1)\(T(1)\)是一条长度为\(p\)的链: (2)\(T(2)\)是一条长度为\(q\)的链: (3)\(T(i)\)是一棵二叉树,它的左子 ...
随机推荐
- 使用dynamic特性处理XML文档
处理XML文档是我们经常需要进行的一项工作,尤其是在进行网络服务相关编程时,比如更新RSS等.在.NET 3.5中引入了Linq To XML,使得XML文档的读写已经大大简化,而.NET 4.0中最 ...
- Linux ext2文件系统之初步思考
数据存放在磁盘中,磁盘最小存取单位sector(512Byte);文件系统中存储的最小单位是 块(Block),大小通常(1KB,2KB,4KB...), 一个block对应多个sector,因而可用 ...
- java中的内存溢出和内存泄漏
内存溢出:对于整个应用程序来说,JVM内存空间,已经没有多余的空间分配给新的对象.所以就发生内存溢出. 内存泄露:在应用的整个生命周期内,某个对象一直存在,且对象占用的内存空间越来越大,最终导致JVM ...
- PullToRefreshListView插件初次进入页面自动刷新
只要将PullToRefreshListView源码中的: @Override protected void onRefreshing(final boolean doScroll) { /** * ...
- npm -v;报错 cannot find module "wrapp"
1.node -v正常.npm-v就报错.. 说明:在官网上下载了安装了好几次.一用到npm就报这个错.园友们,我不太懂node,你们遇到这个问题怎么解决的? 2.报错 cannot find mod ...
- django 前端请求跨域问题解决
django 前端请求跨域问题解决 笔者之前在做django-restful-api开发的时候,在前端请求页面发送请求的时候直接出现301,域名重定向的问题,经过一番查阅资料,终于得到了非常完美的解决 ...
- 基于Jquery UI的autocompelet改写,自动补全控件,增加下拉选项,动态设置样式,点击显示所有选项,并兼容ie6+
Jquery UI的autocompelete改写 注意:实现功能,除了原版的自动补全内容外,增加一个点击显示所有选项,样式能动态设置. 加载数据的来源为后台数据库读取. 具体代码如下: 引用 从官方 ...
- 赢在面试之Java泛型篇(十二)
139. Java中的泛型是什么 ? 使用泛型的好处是什么? 泛型是Java SE 1.5的新特性,泛型的本质是参数化类型,也就是说所操作的数据类型被指定为一个参数. 好处: 1.类型安全,提供编译期 ...
- Luogu P1073 最优贸易
题目描述 C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市.任意两个城市之间最多只有一条道路直接相连.这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双 ...
- NodeMCU Builder, yet another NodeMCU IDE
最近几天研究基于NodeMCU的Wi-Fi小车,突然之间想要写一个专门开发NodeMCU Lua代码的工具自己用,由于官方已经有了NodeMCU Studio,所以我的就叫NodeMCU Builde ...
