局部权重线性回归(Locally weighted linear regression)
在线性回归中，因为对參数个数选择的问题是在问题求解之前已经确定好的，因此參数的个数不能非常好的确定，假设參数个数过少可能拟合度不好，产生欠拟合(underfitting)问题，或者參数过多，使得函数过于复杂产生过拟合问题(overfitting)。因此本节介绍的局部线性回归(LWR)能够降低这种风险。
欠拟合与过拟合
首先看以下的图
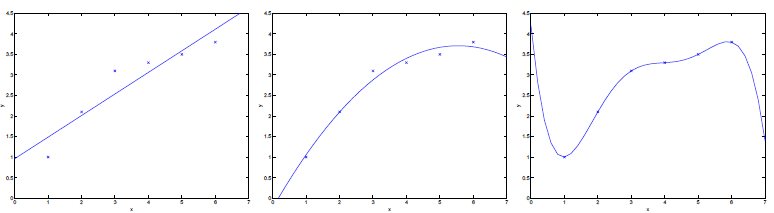
对于图中的一系列样本点，当我们採用y=θ0+θ1x形式的时候，我们可能产生最左边图形式的拟合曲线；假设我们採用y=θ0+θ1x+θ2x2时候，我们就能够产生中间的拟合曲线；假设採用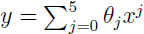
形式，便会产生最右边的拟合曲线。从三张图中我们能够看出来，第一条曲线存在欠拟合问题，第三条的曲线存在过拟合问题。
局部权重线性回归(Locally weighted linear regression)
在主要的线性回归问题中，首先我们构造出预測函数h(x)，然后变化參数θ使得误差函数最小化，一旦θ确定，以后不会改变，全部的预測值都会使用着一个參数：
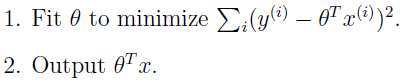
相比之下，局部权重线性回归方法运行例如以下的算法：
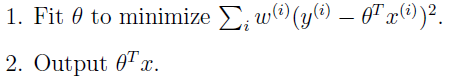
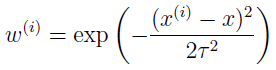
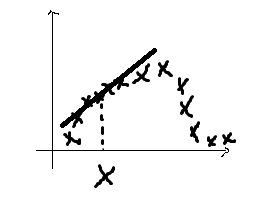
x代表须要预測的值的输入，x(i)表示的是训练的样本的输入值。从w(i)的表达式我们能够看出，（x(i)−x）2能够理解成训练值与预測值之间的距离，当距离越大w≈0，反之，距离越小，w≈1。因此，当距离须要计算的x非常远的训练样本值会在最小化时候变为0，而仅仅使用x周围的局部点预測线性函数。例如以下图
w中的τ称为带宽(bandwidth)參数,能够控制x周围的概念，即控制距离x多远能够參与线性函数的预计，τ越大，參与的点越多，反之，參与的点越少。
因为局部权重线性回归方法每个预測每个点时候都须要又一次计算一次
θ的值，因此，算法费时间复杂度会非常高，是一种non-parametric算法。前面的基本线性回归是一种parametric学习算法。
局部权重线性回归(Locally weighted linear regression)的更多相关文章
- 局部加权线性回归(Locally weighted linear regression)
首先我们来看一个线性回归的问题,在下面的例子中,我们选取不同维度的特征来对我们的数据进行拟合. 对于上面三个图像做如下解释: 选取一个特征,来拟合数据,可以看出来拟合情况并不是很好,有些数据误差还是比 ...
- Locally Weighted Linear Regression 局部加权线性回归-R实现
局部加权线性回归 [转载时请注明来源]:http://www.cnblogs.com/runner-ljt/ Ljt 作为一个初学者,水平有限,欢迎交流指正. 线性回归容易出现过拟合或欠拟合的问 ...
- Locally weighted linear regression(局部加权线性回归)
(整理自AndrewNG的课件,转载请注明.整理者:华科小涛@http://www.cnblogs.com/hust-ghtao/) 前面几篇博客主要介绍了线性回归的学习算法,那么它有什么不足的地方么 ...
- 局部加权回归、欠拟合、过拟合（Locally Weighted Linear Regression、Underfitting、Overfitting）
欠拟合.过拟合 如下图中三个拟合模型.第一个是一个线性模型,对训练数据拟合不够好,损失函数取值较大.如图中第二个模型,如果我们在线性模型上加一个新特征项,拟合结果就会好一些.图中第三个是一个包含5阶多 ...
- 线性回归模型（Linear Regression）及Python实现
线性回归模型(Linear Regression)及Python实现 http://www.cnblogs.com/sumai 1.模型 对于一份数据,它有两个变量,分别是Petal.Width和Se ...
- 贝叶斯线性回归（Bayesian Linear Regression）
贝叶斯线性回归(Bayesian Linear Regression) 2016年06月21日 09:50:40 Duanxx 阅读数 54254更多 分类专栏: 监督学习 版权声明:本文为博主原 ...
- 机器学习：线性回归法（Linear Regression）
# 注:使用线性回归算法的前提是,假设数据存在线性关系,如果最后求得的准确度R < 0,则说明很可能数据间不存在任何线性关系(也可能是算法中间出现错误),此时就要检查算法或者考虑使用其它算法: ...
- 多元线性回归（Multivariate Linear Regression）简单应用
警告:本文为小白入门学习笔记 数据集: http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearnin ...
- 斯坦福CS229机器学习课程笔记 Part1：线性回归 Linear Regression
机器学习三要素 机器学习的三要素为:模型.策略.算法. 模型:就是所要学习的条件概率分布或决策函数.线性回归模型 策略:按照什么样的准则学习或选择最优的模型.最小化均方误差,即所谓的 least-sq ...
随机推荐
- asp.net ajax 检测用户名是否可用代码
原文 asp.net ajax 检测用户名是否可用代码 .net ajax 检测用户名是否可用代码 <script type="text/网页特效" src="c ...
- iot表和heap表排序规则不同
SQL> select * from (select * from t1 order by id ) where rownum<20; ID A1 A2 A3 ---------- --- ...
- ORACLE 五种表的优缺点总结
ORACLE 五种表的优缺点总结: 1.普通表(heap table):适合大部分设计场景,有长处也有缺点. 长处: a,语法简单方便 b,适合大部分场景 缺点: a,更新日志开销较大 b,Delet ...
- MVC3和MVC4中CRUD操作
MVC3中EF实现的CRUD操作 public class HomeController : Controller { // // GET: /Home/ CarModelContainer db = ...
- Swift - 本地数据的保存与加载（使用NSCoder将对象保存到.plist文件）
下面通过一个例子将联系人数据保存到沙盒的“documents”目录中.(联系人是一个数组集合,内部为自定义对象). 功能如下: 1,点击“保存”将联系人存入userList.plist文件中 2,点击 ...
- HDU 2152 Fruit (母函数)
# include<stdio.h> # include <algorithm> # include <string.h> # include <iostre ...
- Mysql对自增主键ID进行重新排序
Mysql数据库表的自增主键ID号经过一段时间的添加与删除之后乱了,需要重新排列. 原理:删除原有的自增ID,重新建立新的自增ID. 1,删除原有主键: ALTER TABLE `table_name ...
- ajax文本空输入显示用户信息
一般文件代码 public void ProcessRequest (HttpContext context) { //获取主见值 string s = context.Request["u ...
- CArray
CArray是windows下的相当于动态数组的模板类.用起来及其方便,近期由于需要在JNI下的C语言中使用,自己参考CArray类函数,及其自己需要使用到的部分函数用C++实现出来,以供自己使用,在 ...
- Missing artifact net.sf.json-lib:json-lib:jar:2.2.3:compile
json-lib是需要区分jdk版本的,pom.xml中的配置应加上<classifier>标签,如用jdk15: <dependency> <groupId>ne ...