[Optimization] Dynamic programming

“就是迭代，被众人说得这么玄乎"

“之所以归为优化，是因为动态规划本质是一个systemetic bruce force"

“因为systemetic，所以比穷举好了许多，就认为是优化的功绩咯"

一个热身问题

不等长活动的安排

活动不等长，安排利用率最高的活动安排。

不同于“贪心算法”的例子，这里希望活动地点的时间利用率尽量的满，而不是“为满足更多的活动”。

三个例子：

T(1) = f1-s1

T(2) = f2-s2

T(3) = T(1) + f3-s3，包含了子问题T(1)；

核心思维：

T(3)时，就要优先保留住f3-s3，然后再看其他"不冲突的items"；这些"不冲突的items"其实是个之前的子问题。

T(n) 不一定是最大，所以，最后要找出Table中的T(1)->T(n)中最大的，即是最优的。

进化而来的 "动态规划"

最长公共子序列法（LCS）

寻找子问题的思想

Ref: http://www.cnblogs.com/liyukuneed/archive/2013/05/22/3090597.html

动态规划，众所周知，第一步就是找子问题，也就是把一个大的问题分解成子问题。

A = "a0, a1, a2, ..., am-1"，

B = "b0, b1, b2, ..., bn-1"。

如果am-1 == bn-1，则当前最长公共子序列为"a0, a1, ..., am-2"与"b0, b1, ..., bn-2"的最长公共子序列与am-1的和。长度为"a0, a1, ..., am-2"与"b0, b1, ..., bn-2"的最长公共子序列的长度+1。

　　// 尾巴一样，那肯定可以直接考虑“子问题”；

如果am-1 != bn-1，则最长公共子序列为max（"a0, a1, ..., am-2"与"b0, b1, ..., bn-1"的公共子序列，"a0, a1, ..., am-1"与"b0, b1, ..., bn-2"的公共子序列）

　　// 尾巴如果不一样，你的尾巴可能是我的倒数第二个；我的尾巴也可能是你的倒数第二个；二者找一个最大的就好；

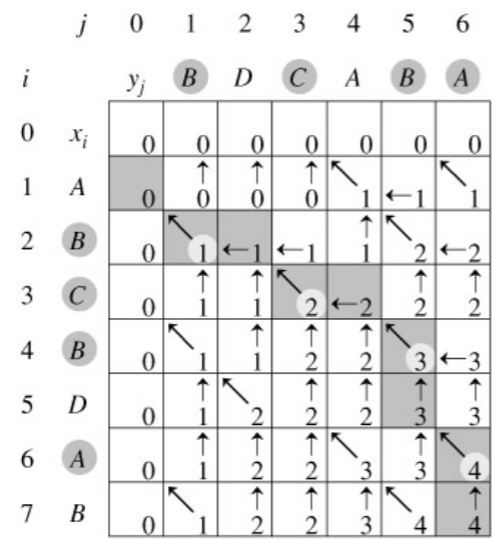
可视化为“二维数组”

按照动态规划的思想，对问题的求解，其实就是对子问题自底向上的计算过程。

这里，计算c[i][j]时，c[i-1][j-1]、c[i-1][j]、c[i][j-1]已经计算出来了，这样，我们可以根据X[i]与Y[j]的取值，按照上面的递推，求出c[i][j]，同时把路径记录在b[i][j]中（路径只有3中方向：左上、左、上，如下图）。

最长递增子序列（LIS）

Ref: 最长递增子序列

给定一个长度为N的数组，找出一个最长的单调自增子序列（不一定连续，但是顺序不能乱）。

例如：

给定一个长度为6的数组A{5， 6， 7， 1， 2， }，则其最长的单调递增子序列为{5，6，7，8}，长度为4.

解法一：利用LCS法

可以把上面的问题转化为求最长公共子序列的问题。

(1) 排序A ----> 得到子序列 B。

(2) A和B求LCS即可。

解法二：naive迭代法 O(N^2)

时间复杂度：从前到后遍历每一个elem，每一elem都要与之前的所有i 做比较，这样时间复杂度为O(N^2)。

这是简单粗暴的方法。

解法三：动态规划法 O(NlogN)

假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7，可以看出来它的LIS长度为5。

下面一步一步试着找出它。

我们定义一个序列B，然后令 i = 1 to 9 逐个考察这个序列。

此外，我们用一个变量Len来记录现在最长算到多少了。

// 注意下面的“淘汰掉5”的过程

首先，把d[1]有序地放到B里，令B[1] = 2，就是说当只有len=1 一个数字2的时候，长度为1的LIS的最小末尾是2。这时Len=1

然后，把d[2]有序地放到B里，令B[1] = 1，就是说长度为1的LIS的最小末尾是1，d[1]=2已经没用了，很容易理解吧。这时Len=1

接着，d[3] = 5，d[3]>B[1]，所以令B[1+1]=B[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，很容易理解吧。这时候B[1..2] = 1, 5，Len＝2

再来，d[4] = 3，它正好加在1,5之间，放在1的位置显然不合适，因为1小于3，长度为1的LIS最小末尾应该是1，这样很容易推知，长度为2的LIS最小末尾是3，于是可以把5淘汰掉，这时候B[1..2] = 1, 3，Len = 2

继续，d[5] = 6，它在3后面，因为B[2] = 3, 而6在3后面，于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6，还是很容易理解吧？ Len = 3 了噢。

第6个, d[6] = 4，你看它在3和6之间，于是我们就可以把6替换掉，得到B[3] = 4。B[1..3] = 1, 3, 4， Len继续等于3

第7个, d[7] = 8，它很大，比4大，嗯。于是B[4] = 8。Len变成4了

第8个, d[8] = 9，得到B[5] = 9，嗯。Len继续增大，到5了。

最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，所以我们知道，最新的B[4] =7，B[1..5] = 1, 3, 4, 7, 9，Len = 5。

于是我们知道了LIS的长度为5，且此时最后一个数字应该是 9。【有了这个线索，倒着遍历，发现9后，就可以过滤出想要的序列了】

注意。这个1,3,4,7,9不是LIS，它只是存储的对应长度LIS的最小末尾。有了这个末尾，我们就可以一个一个地插入数据。

虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义，但是如果后面再出现两个数字 8 和 9，那么就可以把8更新到d[5], 9更新到d[6]，得出LIS的长度为6。

然后应该发现一件事情了：在B中插入数据是有序的，而且是进行替换而不需要挪动——也就是说，我们可以使用二分查找，将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)

分解 “子问题”

硬币找零

如果我们有面值为1元、3元和5元的硬币若干枚，如何用最少的硬币凑够11元？

思维方式

首先我们思考一个问题，如何用最少的硬币凑够i元(i<11)？

1. 当我们遇到一个大问题时，总是习惯把问题的规模变小，这样便于分析讨论。

2. 这个规模变小后的问题和原来的问题是同质的，除了规模变小，其它的都是一样的，本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。

初始化

当i=0，即我们需要多少个硬币来凑够0元。由于1，3，5都大于0，即没有比0小的币值，因此凑够0元我们最少需要0个硬币。

我们用 d(i)=j 来表示凑够i元最少需要j个硬币。

于是我们已经得到了 d(0)=0，表示凑够0元最小需要0个硬币。

当i=1时，只有面值为1元的硬币可用，因此我们拿起一个面值为1的硬币，接下来只需要凑够0元即可，而这个是已经知道答案的，即 d(0)=0。

所以，d(1)=d(1-1)+1=d(0)+1=0+1=1。

当i=2时，仍然只有面值为1的硬币可用，于是我拿起一个面值为1的硬币，接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量)，而这个答案也已经知道了。

所以d(2)=d(2-1)+1=d(1)+1=1+1=2。

当i=3时，我们能用的硬币就有两种了：1元的和3元的。既然能用的硬币有两种，我就有两种方案。

如果我拿了一个1元的硬币，我的剩下的目标就变为了：凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。

如果我拿了一个3元的硬币，我的剩下的目标就变为了：凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1。

状态转移方程

这两种方案哪种更优呢？记得我们可是要用最少的硬币数量来凑够3元的。

所以，选择d(3)=1，怎么来的呢？具体是这样得到的：d() = min{d(-1)+1, d(-3)+1}。

可见，这边形成了一个三叉树（因为有三种情况1，3，5），而子问题就是当前问题的孩子，这些孩子已有了局部结果，直接用即可。

d(n) = min{ d(n-x_i)+1 | i = types of coin}

巨量的子问题

理解：N(i,j) = N(i,j-i) + N(i-1, j)

以上只是求最优的一个解，即：最少的coin的方案。这其实是很多种组合中的一个。

那么，本来有多少种组合呢？（有点像“没有上级的宴会邀请问题”）

N(i, j)

i:使用的面值最大的coin
j:要构成的总价值

N(1, 1000) : 只有一种方案。

N(2, 1000) : 有好多种方案，很多很多，怎么算呢？

N(3, 1000) : 有更多种方案，很多很多，怎么算呢？

/* 一定使用i,即至少有一个i, 那么，剩下的价值最大的可能（bound）就是j-i。

* 不会使用i,会有多少种方案，这个子问题会提前被解。

N(i,j) = N(i,j-i) + N(i-1, j)

N(i,j) = N(i,j-i) + N(i-1, j)
N(3,1000) = N(3,997) + N(2, 1000)
N(3,997)				N(2, 1000)
N(3,994)		N(2, 997)		N(2,998)		N(1, 1000)
N(3,991)	N(2,994)	N(2,995)	N(1,997)	N(2,996)	N(1,998)
N(3,988); N(2,991)	N(2,992); N(1,994)	N(2,993); N(1,995)		N(2,994); N(1,996)
...	...	...		...

可见，最后结果是个极其庞大的数字。

感性理解

为何 N(2, 1000) = N(2, 998) + N(1, 1000) ?

假设1000不是全部由1构成，那么，出现在其中的2就肯定可以移动到顶端。

又因为这里是考虑的组合问题，而不是排列，所以，出现的2的这种情况就肯定能由x个左边的情况中的一种所表示。

其实就是：有2，或者没2；如果有2，那就等于1000减去这个2；

这个思维，与"叠海龟问题"中的”w+s最大的肯定能放在最下面“的思想是一致的。

再次理解 “子问题”

Devise a dynamic programming algorithm that counts the number of non-decreasing
sequences of integers of length N, such that the numbers are between 0 and M
inclusive.

举例：

#（3，2）表示：用数字1和2（条件是<=2）构成的len <=3的非递减序列有多少种？

1,1

1,2

2,2

1,1,1

1,1,2

1,2,2

2,2,2

#（5，10）= #（4，10）+ #（5，9）

考虑10时，

等号右侧左变量：有10，10已占坑，只需考虑剩下前四个即可#（4，10）。
等号右侧右变量：没10，最大只能是9，5个数字要从10前面的item里选择。

子问题变成了只能向右下角（终点）推进的二维数组模式。

进一步练习

背包问题

Integer Knapsack Problem (Duplicate Items NOT Allowed)

You have n items (some of which can be identical); item Ii is of weight wi and value vi.
You also have a knapsack of capacity C. Choose a combination of available items

which all fit in the knapsack and whose value is as large as possible.

Matrix 的横轴纵轴表示

子问题的表达：左黄到右黄 or 左黄到右下蓝

矩阵解释

数组f[i][j]：在只有i个物品，容量为j的情况下背包问题的最优解.

当物品种类变大为i+1时，最优解是什么？

第i+1个物品，假设：

- 能放进背包（前提是放得下），那么f[i+1][j]= f[i][j-weight[i+1]+value[i+1]；
- 如果不放进背包，那么f[i+1][j]= f[i][j]。

这就得出了状态转移方程：

f[i+1][j]=max( f[i][j], f[i][j-weight[i+1]+value[i+1] )。

手动举例子

From: http://blog.csdn.net/mu399/article/details/7722810

条件：

- 有编号分别为a,b,c,d,e的五件物品，
- 它们的重量分别是2,2,6,5,4，
- 它们的价值分别是6,3,5,4,6，
- 现在给你个承重为10的背包，

如何让背包里装入的物品具有最大的价值总和？

现考虑 a4：

此时考虑a，但放不下了（此时的value=6是因为放了v(e) = 6）

接下来自然会想，是不是换一下袋子里的这个东东，能获得更大的value呢？此时，表格对子问题的记录就发挥作用了！

直接看sub-p:b2，看起来4-2->2有点自动导航到所需子问题的味道。

结果是：你要分要放得下a，那么，能得到value为9这个方案。这个方案看起来更好呦。

所以，思维的关键就是要不要a的时候，看看两种不同情况下的value就好了。

Extended:

if Duplicate items allowed.

P = NP, 只能穷举。

Extended:

数字分组问题，将问题转化为求背包容量为所有数总和一半的背包问题。

生产线装配问题

问题描述

下图中可以看出按照红色箭头方向进行装配汽车最快，时间为38。分别现在装配线1上的装配站1、3和6，装配线2上装配站2、4和5。

寻找子问题

(1) 描述通过工厂最快线路的结构

对于装配线调度问题，一个问题的（找出通过装配站S_i,j的最快线路）最优解包含了子问题（找出通过S_1,j-1或S_2,j-1的最快线路）的一个最优解，这就是最优子结构。

观察一条通过装配站S_1,j(在装配线1上) 的最快线路，会发现它必定是经过装配线1或2上装配站j-1。因此通过装配站的最快线路只能以下二者之一：

　　a) 通过装配线S_1,j-1的最快线路，然后直接通过装配站S_i,j；

　　b) 通过装配站S_2,j-1的最快线路，从装配线2移动到装配线1，然后通过装配线S_1,j。

为了解决这个问题，即寻找通过一条装配线上的装配站j的最快线路，需要解决其子问题，即寻找通过两条装配线上的装配站j-1的最快线路。

(子问题有两条路线罢了)

(2) 一个递归的解

最终目标是确定底盘通过工厂的所有路线的最快时间，设为f*，令f_i[j]表示一个底盘从起点到装配站S_i,j的最快时间，

则f* = min(f₁[n]+x₁, f₂[n]+x₂)。逐步向下推导，直到j=1。

- 当j=1时：
  - f₁[1] = e₁+a_1,1, f₂[1] = e₂+a_2,1。
- 当j>1时：
  - f₁[j] = min(f₁[j-1]+a_1,j， f₂[j-1]+t_2,j-1+a_1,j)，
  - f₂[j] = min(f₂[j-1]+a_2,j， f₁[j-1]+t_1,j-1+a_2,j)。

Link: http://www.cnblogs.com/aabbcc/p/6509191.html

矩阵连乘

To evaluate (AB)C we need
(10 × 5) × 100 + (10 × 50) × 5 = 5000 + 2500 = 7500 multiplications;
To evaluate A(BC) we need
(100 × 50) × 5 + (10 × 50) × 100 = 25000 + 50000 = 75000 multiplications!

如何使计算量最小？

Ref: https://cnbin.github.io/blog/2015/12/19/ju-zhen-lian-cheng-dong-tai-gui-hua-xiang-jie/

最优子结构

(1) 找出最优解的性质，刻画其特征结构

令 m[i][j] 表示第i个矩阵至第j个矩阵这段的最优解。从 i --> j

将矩阵连乘积简记为A[i:j] ，这里i<=j。

假设这个最优解在第k处断开，i<=k<j，因为A[i:j]是最优的，那么A[i,k]和A[k+1:j]也是相应矩阵连乘的最优解。　　// <-- 整体最优，内部分割也最优

可以用反证法证明之。这就是最优子结构，也是用动态规划法解题的重要特征之一。

(2) 建立递归关系

设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n] 。

当i=j时，A[i,j]=Ai, m[i,j]=0;(表示只有一个矩阵,如A1,没有和其他矩阵相乘，故 乘的次数为0)
当i<j时，m[i,j] = min{ m[i,k] + m[k+1,j] + p_i-1*p_k*p_j} , 其中 i<=k<j

相当于对i~j这段，把它分成2段，看哪种分法乘的次数最少，如：

A1,A2,A3,A4,则有3种分法:{A1}{A2A3A4}、{A1A2}{A3A4}、{A1A2A3}{A4}，

其中，{}表示其内部是最优解，如{A1A2A3}表示是A1A2A3的最优解。

实践出真知

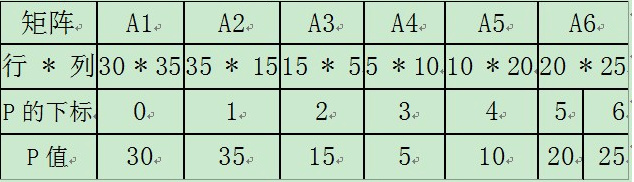
对于 p={30, 35, 15, 5, 10, 20, 25}:

计算顺序

每个对角线算是一组；总共有如下六组。

表中是可能的所有组合情况，需要计算选出每个表格中最小的一个组合方式。

“左下”的计算就将成为“右上”计算的子问题集合！

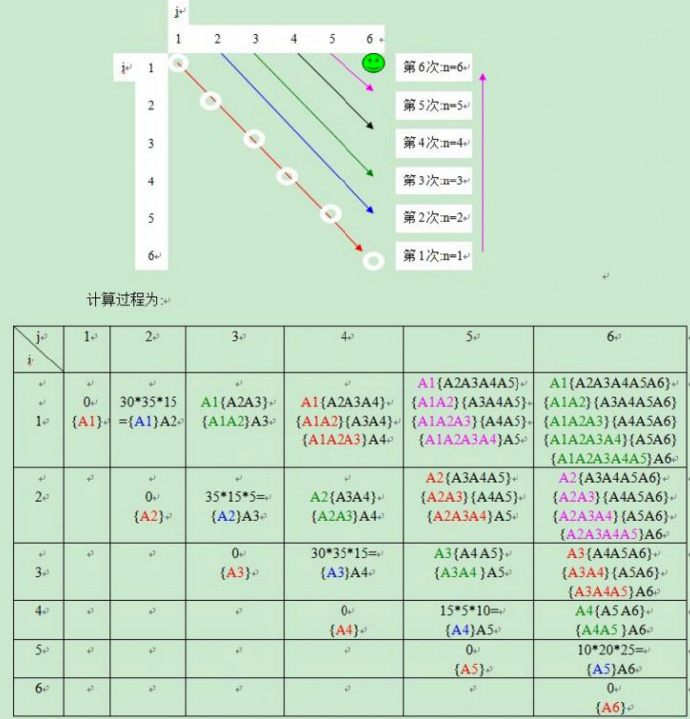
对上例,共6个矩阵(A1~A6)，n=6,

当r=3时，r循环里面的是3个矩阵的最优解，i 从1->4，即求的是 (r=3时对角线是共四种情况)

(A1 A2 A3), (A2 A3 A4), (A3 A4 A5), (A4 A5 A6) 这4个矩阵段 (长度为3) 的最优解.

当i=2时，(A2 A3 A4) 的最优解为 { A2 (A3 A4) , (A2 A3) A4 } 的较小值。

思维技巧

花括号里的东西不用计算了，因为之前已经计算过了，只需要查表找到最优的方式，以及min value直接用即可。

Graph 的路径问题

Bellman-Ford算法

单源头最短路径，支持负权值

Ref: 几个最短路径算法Floyd、Dijkstra、Bellman-Ford、SPFA的比较

Dijkstra Algorithm

Dijkstra Algorithm Video: https://www.youtube.com/watch?v=RFEqcXSo_Zg

Dijkstra 算法采用贪心算法（Greedy Algorithm）范式进行设计，普通实现的时间复杂度为 O(V²)，

若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)。

Bellman-Ford Algorithm

Bellman-Ford Algorithm 和 Dijkstra 算法同为解决单源最短路径的算法。对于带权有向图 G = (V, E)，

- Dijkstra 算法要求图 G 中边的权值均为非负。　　// 基于贪心算法，普通实现的时间复杂度为 O(V²)，若基于 Fibonacci heap 的最小优先队列实现版本则时间复杂度为 O(E + VlogV)
- Bellman-Ford 算法能适应一般的情况（即存在负权边的情况）。　　// 基于动态规划，O(V*E)

一个实现的很好的 Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。

Bellman-Ford 算法采用动态规划（Dynamic Programming）进行设计，实现的时间复杂度为 O(V*E)，其中 V 为顶点数量，E 为边的数量。

Bellman-Ford 讲解

油管讲解: Bellman-Ford Algorithm Explained EASY

此链接讲得很明了。例如：

iteration: 3 D --> 7

// 建立在“子问题”之上，也就是上一个“列”。

S走三步到D，那么当然从上一次iter的两步的基础之上考虑！

上一轮中"非无限"的，有哪些直达D呢？(下图所示)
- C直达，且第二次iter时C=5，所以，5+2=7成为relax后的新值。
- F直达，且第二次iter时C=4，但是，4+3=7成为relax后的新值，以上面的新值一样。
再看下一个E。

可见这里体现了时间复杂度为O(V*E)，就是矩阵的格子数。

【横轴：从S开始走几步能到达某个结点】

结果

最终的结果就是最后一列。

后一列比前一列更“优化”，值也就更“小”。

采用队列继续优化

Bellman-ford算法浪费了许多时间去做没有必要的松弛，

而 SPFA算法用队列进行了优化，效果十分显著，高效难以想象。(后续再研究)

Floyd Warshall Algorithm

多源最短路径求法? 点击图片进入视频链接。

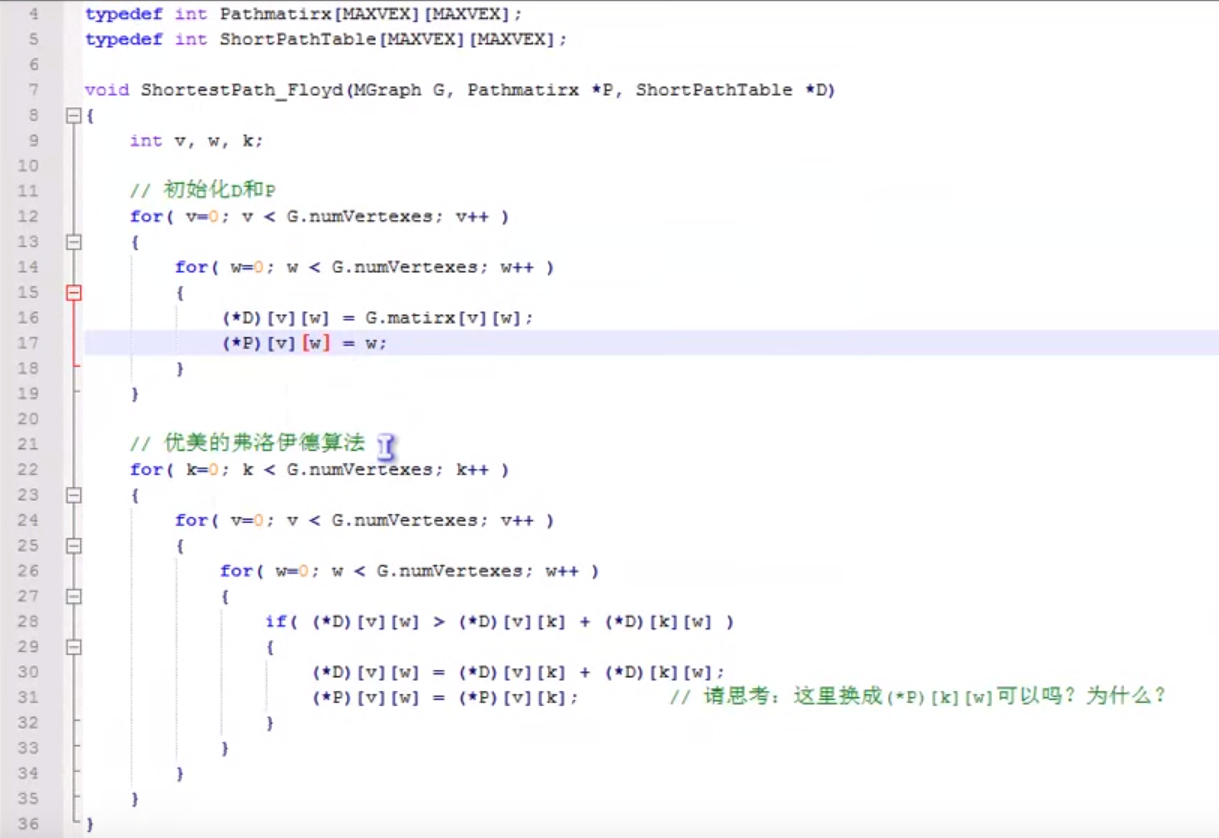
初始状态

Ref: 65 小甲鱼数据结构与算法最短路径（弗洛伊德算法）

P矩阵告诉我们：从v_x到v_y时必须要经过哪个点。

时间复杂度O(n^3)

最终状态

课后练习

Edit Distance

字符串变换的”最少操作“：

Given two text strings A of length n and B of length m, you
want to transform A into B. You are allowed to insert a character, delete a
character and to replace a character with another one. An insertion costs ci, a
deletion costs cd and a replacement costs cr.
Task: find the lowest total cost transformation of A into B

Ref: http://www.cnblogs.com/masterlibin/p/5785092.html

子问题：

Maximizing an expression

Instance: a sequence of numbers with operations +, −, × in between, for example
　　1 + 2 − 3 × 6 − 1 − 2 × 3 − 5 × 7 + 2 − 8 × 9
Task: Place brackets in a way that the resulting expression has the largest possible
value.

Ref: https://courses.csail.mit.edu/6.006/fall10/psets/ps6/ps6-sol.pdf

答案：有点复杂，详见链接。

Extended:

逻辑表达式中插入符号，使结果为true。求有多少种方式。

上图为子问题：T(i, j) 的表达方式。

子问题看上去也得有O(n^2)个regression。

子字符串（隐含）出现的次数

We say that a sequence of Roman letters A occurs as a subsequence of a sequence
of Roman letters B if we can obtain A by deleting some of the symbols of B. Design
an algorithm which for every two sequences A and B gives the number of different
occurrences of A in B, i.e., the number of ways one can delete some of the symbols
of B to get A. For example, the sequence ba has three occurrences in the sequence
baba: baba, baba, baba.

From: https://stackoverflow.com/questions/6877249/find-the-number-of-occurrences-of-a-subsequence-in-a-string

Idea:

Based on Suffix matching.

The subproblem is to give the number of different occurences of substring of A in substring of B. (A的后缀字符串在B的后缀字符串出现的次数)

Algorithm:

- In
  cell [row][col]
  write the value found at [row-1][col].
- If
  sequence at row row
  and
  subsequence
  at column col
  start
  with the same char,
  add the value found at [row-1][col-1]
  to the value just written to [row][col].

求最大子数组的和 in O(n)

给定一个数组,它里面全是一些数字,要找出不论什么连续的值中最大的和. 例: 已有数组:{31, -41, 59, 26, -53, 58, 97, -93, -23, 84}

它的连续的值最大的和则是第 2 个值到第 6 个值的合:187.

如果用函数f(i)表示以第i个数字结尾的子数组的最大和，那么我们需要求出max(f[0...n])。我们可以给出如下递归公式求f(i)

这个公式的意义：

当以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)小于0时，如果把这个负数和第i个数相加，得到的结果反而不第i个数本身还要小，所以这种情况下最大子数组和是第i个数本身。
如果以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)大于0，与第i个数累加就得到了以第i个数结尾的子数组中所有数字的和。

31	-41	59	26	-53	58	97	-93	-23	84
	-10		85	32	90	187	94	71	155
31	-10	59	85	32	90	187	94	71	155

动态规划，众所周知，第一步就是找子问题，也就是把一个大的问题分解成子问题。这里我们设两个字符串A、B，A = "a0, a1, a2, ..., am-1"，B = "b0, b1, b2, ..., bn-1"。