卷积神经网络 cnnff.m程序 中的前向传播算法 数据 分步解析

最近在学习卷积神经网络，哎，真的是一头雾水！最后决定从阅读CNN程序下手！

程序来源于GitHub的DeepLearnToolbox

由于确实缺乏理论基础，所以，先从程序的数据流入手，虽然对高手来讲，这样有点太小儿科了，但觉得对于个人理解CNN网络的结构和数据流走向有较大帮助！

下面，将要分析CNN的前向传播算法cnnff.m

本程序所用的神经网络的结构如下图的结构体net所示

结构体net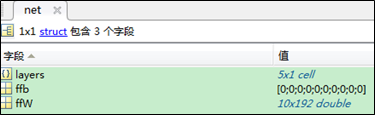
包含5层	每层的结构

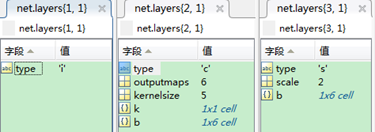
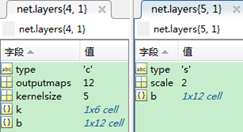
这五层的结构如下：

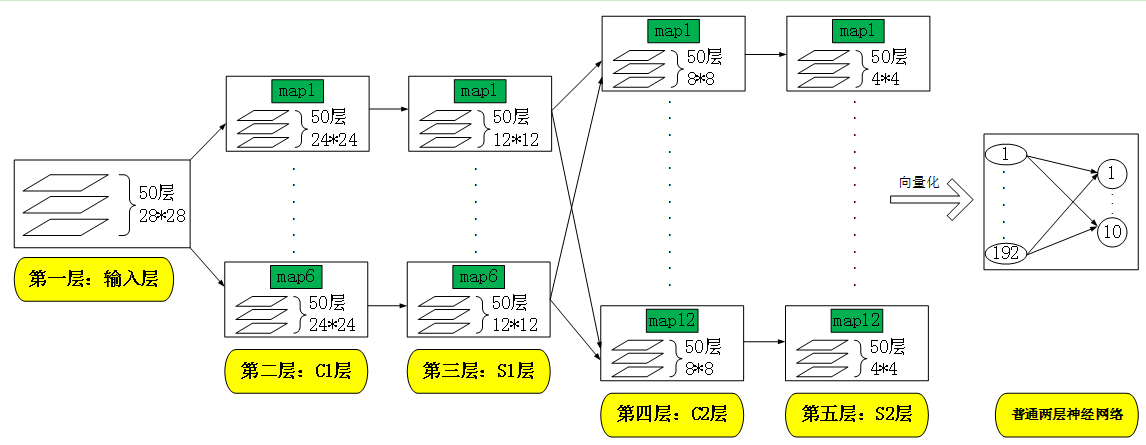
每层的结构分别如下：

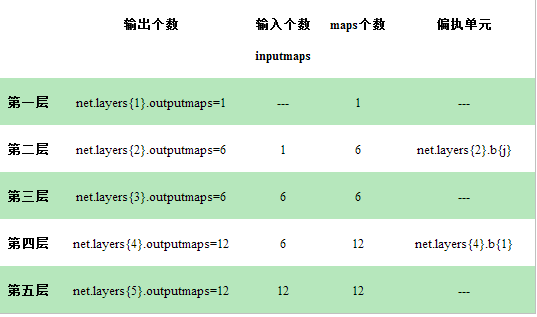
为了方便自己理解，下面，分别对每一层的输入、输出、传播分解介绍

只考虑某一批词的样本

注：所有样本集被分为numbatches批，每一批含有batchsize个样本，对于本程序而言，共有50个样本

 1 第一层到第五层的数据传递

2 第1层到第2层的前面传播（l=2）：卷积操作

利用循环，分别计算第二层每个map的输出：net.layers{2}.a{j} (j=1,..,6)（这里的l=2）

下面，讨论第j次循环时，循环体内部的分步解析

（1）初始化一个三维矩阵z

• z的大小为24*24*50，即第二层中每个map的尺寸
• z存放的是：第二层中每个map的输入

（2）计算第2层第j个map的输入

• 即第1层的所有输出（i=1,…, inputmaps）对第2层的第j个输入的贡献的累加
• z的计算方法是：

  利用第二层的第j个map的卷积核net.layers{2}.k{i}{j}分别对第一层中的第i个map进行卷积运算(i=1,…, net.layers{1}.outputmaps)，并将得到的所有卷积结果相加

  

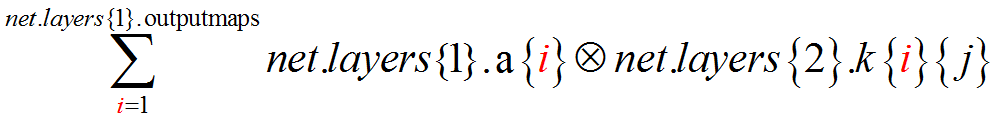
• 第2层的inputmaps=1
• 对net.layers{l}.k{i}{j}进行解释：

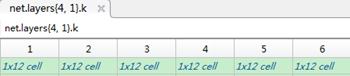
net.layers{l}.k：是一个元胞，有两层

net.layers{l}.k{i}：第l-1层的第i个map到第l层的所有maps的卷积核

net.layers{l}.k{i}{j}：第l-1层的第i个map到第l层的第j个map的卷积核

下面是一个例子：

第四层的卷积核元胞

第3层的第1个map到第4层的所有maps的卷积核（12）个

第3层的第1个map到第四层的第1个maps的卷积核

（3）计算第2层的第j个map的输出

• 第二层的第j个map的输出为net.layers{2}.a{j}=sigm(z+net.layers{l}.b{j})

  即第二层的第j个map的输入z+该map的偏执项后，求sigm函数

（4）对第1层的map进行卷积操作的图例

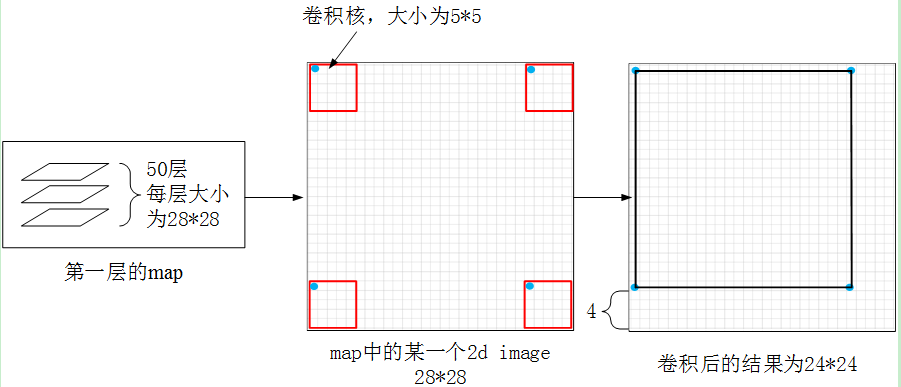
3 第2层到第3层（l=3）：降采样操作

下面，讨论第j次循环时，循环体内部的分步解析

（1）对第二层的第j个map进行卷积运算，得到z

• 利用的卷积核（大小为scale*scale）如下：

  

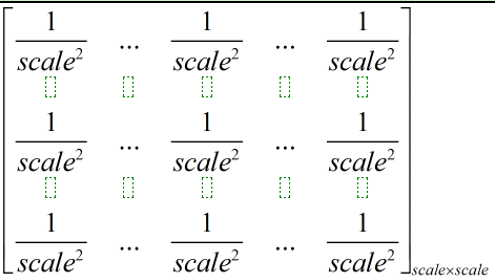
（2）对z进行降采样，得到第三层的第j个map的输出

（3）如上所示的降采样过程示例如下图所示

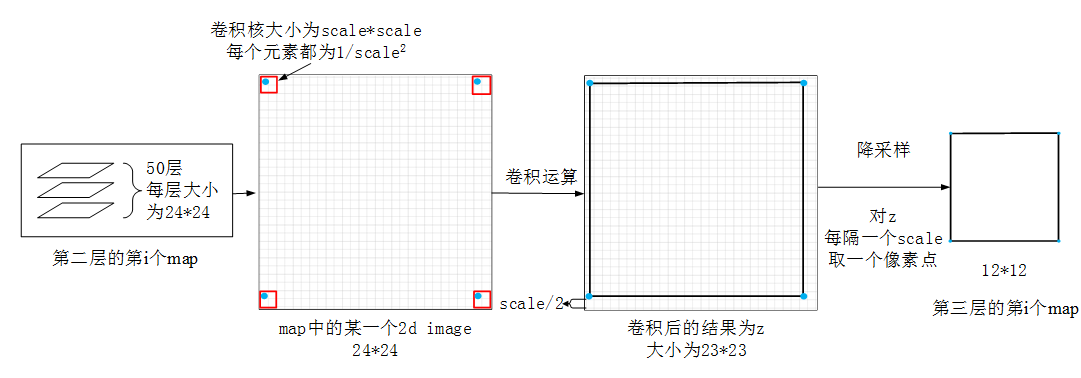
4 第3层到第4层的前面传播（l=4）：卷积操作

利用循环，分别计算第四层每个map的输出：net.layers{4}.a{j} (j=1,..,12)（这里的l=4）

下面，讨论第j次循环时，循环体内部的分步解析

（1）初始化一个三维矩阵z

• z的大小为24*24*50，即第二层中每个map的尺寸
• z存放的是：第四层中每个map的输入

（2）计算第4层的第j个map的输入

• 即第3层的所有输出（i=1,…, inputmaps）对第4层的第j个输入的贡献的累加
• z的计算方法是：

  利用第4层的第j个map的卷积核net.layers{4}.k{i}{j}分别对第3层中的第i个map进行卷积运算(i=1,…, net.layers{1}.outputmaps)，并将得到的所有卷积结果相加

  

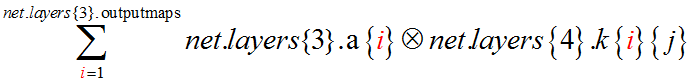
• 第4层的inputmaps=12

（3）计算第4层的第j个map的输出

• 第4层的第j个map的输出为net.layers{4}.a{j}=sigm(z+net.layers{4}.b{j})

  即第4层的第j个map的输入z+该map的偏执项后，求sigm函数

（4）对第3层的map进行卷积操作的图例

5 第4层到第5层 (l=5)：降采样

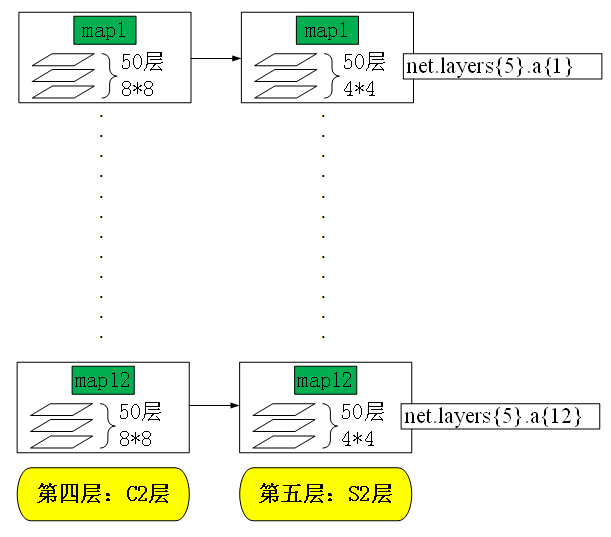
下面，讨论第j次循环时，循环体内部的分步解析

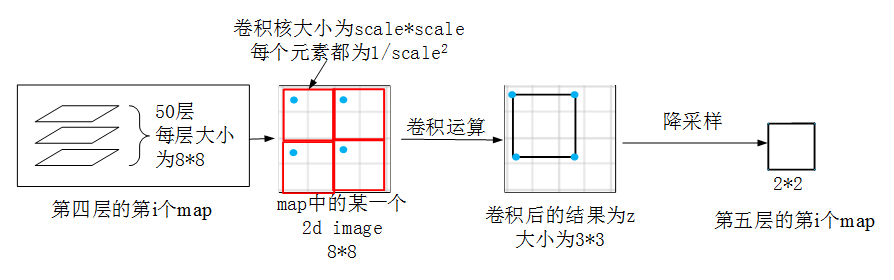
（1）对第四层的第j个map进行卷积运算，得到z

• 利用的卷积核（大小为scale*scale）如下：

  

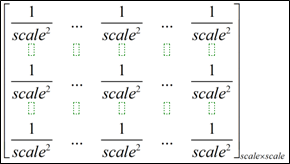
（2）对z进行降采样，得到第五层的第j个map的输出

（3）如上所示的降采样过程示例如下图所示

6 将第五层的map输出向量化

（1）初始化net网络中的fv（其实是新加入fv，原来输入的net中没有fv）

（2）分别对第五层的每个输出map进行向量化（一共用numel(net.layers{n}.a个输出map)

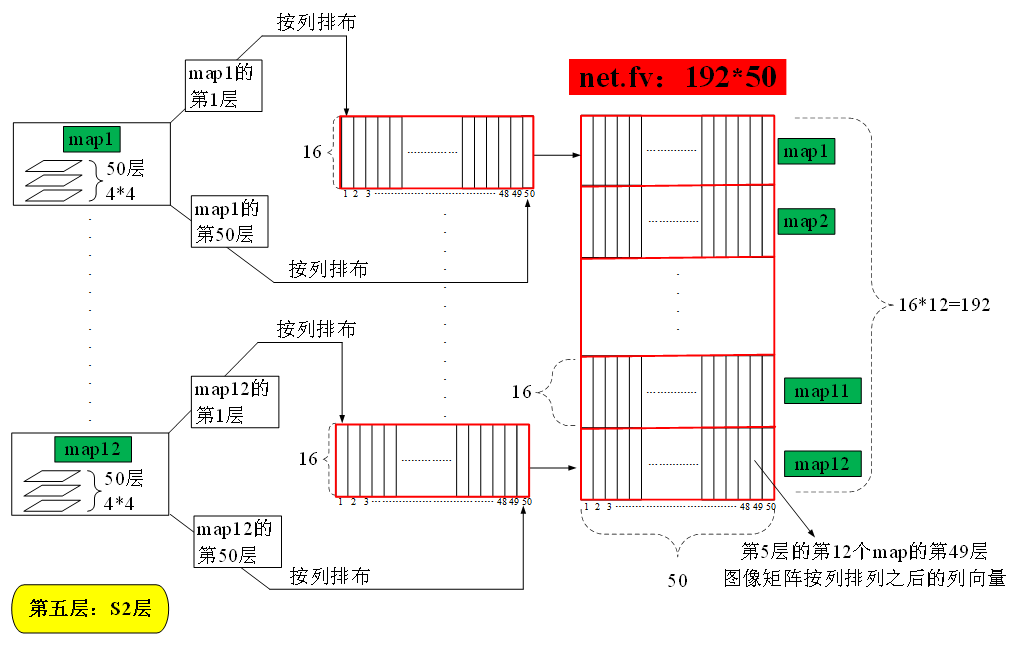
（3）对于第五层的第j个输出map

• 得到第五层第j个输出map的尺寸，应该是三维的，得到的三维尺寸向量存入sa中
• 将第五层的第j个输出map的矩阵转化为一个sa(1)*sa(2)，sa(3)大小的矩阵
• 并将该得到的转化矩阵接入到第五层的第j-1个输出map之后
• 关于矩阵fv的结构如上图所示

7 第五层向量化后传入普通神经网

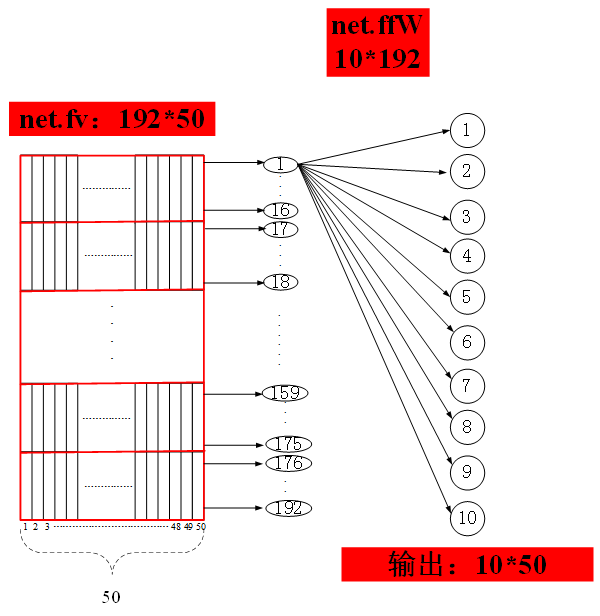
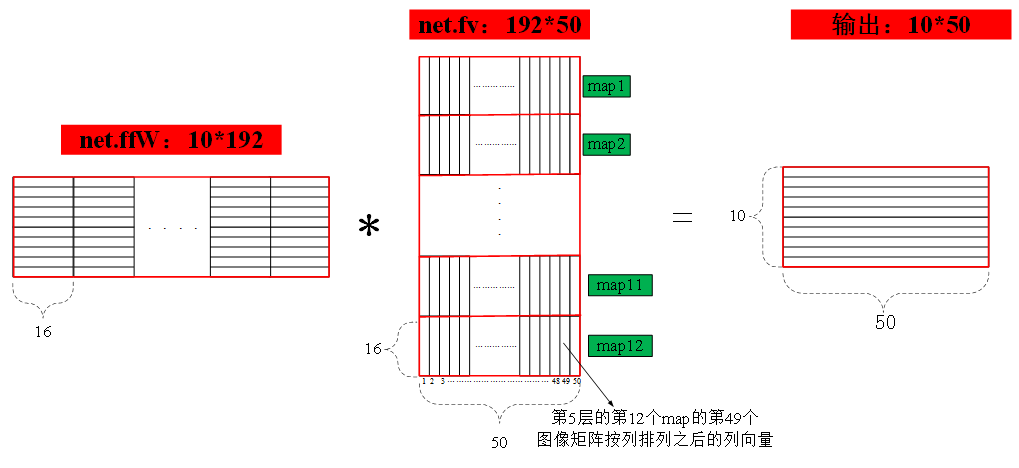
第五层的向量化输出传入一个普通的神经网络，只有输入层和输出层，输入层含有192个神经元，输出层含有10个神经元，输入到输出层的权值矩阵存放在矩阵net.ffW中，在该权值矩阵作用下，该简单神经网络的输出即为最终的整个网络的输出，输出结果存放在net.o矩阵中，该矩阵大小为10*50，每一列分别表示每个输入样本得到的相应的输出