OpenCV支持向量机SVM对线性不可分数据的处理

支持向量机对线性不可分数据的处理

目标

本文档尝试解答如下问题:

• 在训练数据线性不可分时，如何定义此情形下支持向量机的最优化问题。
• 如何设置 CvSVMParams 中的参数来解决此类问题。

动机

为什么需要将支持向量机优化问题扩展到线性不可分的情形？ 在多数计算机视觉运用中，我们需要的不仅仅是一个简单的SVM线性分类器， 我们需要更加强大的工具来解决 训练数据无法用一个超平面分割 的情形。

我们以人脸识别来做一个例子，训练数据包含一组人脸图像和一组非人脸图像(除了人脸之外的任何物体)。 这些训练数据超级复杂，以至于为每个样本找到一个合适的表达 (特征向量) 以让它们能够线性分割是非常困难的。

最优化问题的扩展

还记得我们用支持向量机来找到一个最优超平面。 既然现在训练数据线性不可分，我们必须承认这个最优超平面会将一些样本划分到错误的类别中。 在这种情形下的优化问题，需要将 错分类(misclassification) 当作一个变量来考虑。新的模型需要包含原来线性可分情形下的最优化条件，即最大间隔(margin), 以及在线性不可分时分类错误最小化。

我们还是从最大化 间隔 这一条件来推导我们的最优化问题的模型(这在 前一节 已经讨论了):

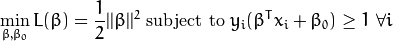
在这个模型中加入错分类变量有多种方法。比如，我们可以最小化一个函数，该函数定义为在原来模型的基础上再加上一个常量乘以样本被错误分类的次数:

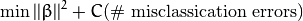
然而，这并不是一个好的解决方案，其中一个原因是它没有考虑错分类的样本距离同类样本所属区域的大小。 因此一个更好的方法是考虑 错分类样本离同类区域的距离:

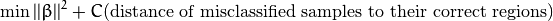
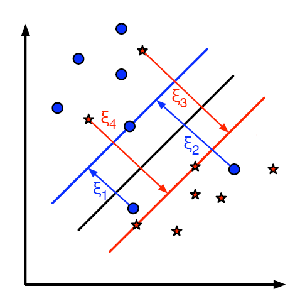
这里为每一个样本定义一个新的参数 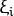 ， 这个参数包含对应样本离同类区域的距离。 下图显示了两类线性不可分的样本，以及一个分割超平面和错分类样本距离同类区域的距离。

Note

图中只显示了错分类样本的距离，其余样本由于已经处于同类区域内部所以距离为零。

红色和蓝色直线表示各自区域的边际间隔， 每个 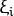 表示从错分类样本到同类区域边际间隔的距离。

最后我们得到最优问题的最终模型:

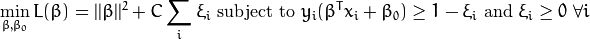
关于参数C的选择， 明显的取决于训练样本的分布情况。 尽管并不存在一个普遍的答案，但是记住下面几点规则还是有用的:

• C比较大时分类错误率较小，但是间隔也较小。 在这种情形下， 错分类对模型函数产生较大的影响，既然优化的目的是为了最小化这个模型函数，那么错分类的情形必然会受到抑制。
• C比较小时间隔较大，但是分类错误率也较大。 在这种情形下，模型函数中错分类之和这一项对优化过程的影响变小，优化过程将更加关注于寻找到一个能产生较大间隔的超平面。

源码

你可以从OpenCV源码库文件夹 samples/cpp/tutorial_code/gpu/non_linear_svms/non_linear_svms 下载源码和视频， 或者 从此处下载.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118

#include <iostream> #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/ml/ml.hpp> #define NTRAINING_SAMPLES 100 // Number of training samples per class #define FRAC_LINEAR_SEP 0.9f // Fraction of samples which compose the linear separable part using namespace cv; using namespace std; int main() { // Data for visual representation const int WIDTH = 512, HEIGHT = 512; Mat I = Mat::zeros(HEIGHT, WIDTH, CV_8UC3); //--------------------- 1. Set up training data randomly --------------------------------------- Mat trainData(2*NTRAINING_SAMPLES, 2, CV_32FC1); Mat labels (2*NTRAINING_SAMPLES, 1, CV_32FC1); RNG rng(100); // Random value generation class // Set up the linearly separable part of the training data int nLinearSamples = (int) (FRAC_LINEAR_SEP * NTRAINING_SAMPLES); // Generate random points for the class 1 Mat trainClass = trainData.rowRange(0, nLinearSamples); // The x coordinate of the points is in [0, 0.4) Mat c = trainClass.colRange(0, 1); rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(0.4 * WIDTH)); // The y coordinate of the points is in [0, 1) c = trainClass.colRange(1,2); rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT)); // Generate random points for the class 2 trainClass = trainData.rowRange(2*NTRAINING_SAMPLES-nLinearSamples, 2*NTRAINING_SAMPLES); // The x coordinate of the points is in [0.6, 1] c = trainClass.colRange(0 , 1); rng.fill(c, RNG::UNIFORM, Scalar(0.6*WIDTH), Scalar(WIDTH)); // The y coordinate of the points is in [0, 1) c = trainClass.colRange(1,2); rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT)); //------------------ Set up the non-linearly separable part of the training data --------------- // Generate random points for the classes 1 and 2 trainClass = trainData.rowRange( nLinearSamples, 2*NTRAINING_SAMPLES-nLinearSamples); // The x coordinate of the points is in [0.4, 0.6) c = trainClass.colRange(0,1); rng.fill(c, RNG::UNIFORM, Scalar(0.4*WIDTH), Scalar(0.6*WIDTH)); // The y coordinate of the points is in [0, 1) c = trainClass.colRange(1,2); rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT)); //------------------------- Set up the labels for the classes --------------------------------- labels.rowRange( 0, NTRAINING_SAMPLES).setTo(1); // Class 1 labels.rowRange(NTRAINING_SAMPLES, 2*NTRAINING_SAMPLES).setTo(2); // Class 2 //------------------------ 2. Set up the support vector machines parameters -------------------- CvSVMParams params; params.svm_type = SVM::C_SVC; params.C = 0.1; params.kernel_type = SVM::LINEAR; params.term_crit = TermCriteria(CV_TERMCRIT_ITER, (int)1e7, 1e-6); //------------------------ 3. Train the svm ---------------------------------------------------- cout << "Starting training process" << endl; CvSVM svm; svm.train(trainData, labels, Mat(), Mat(), params); cout << "Finished training process" << endl; //------------------------ 4. Show the decision regions ---------------------------------------- Vec3b green(0,100,0), blue (100,0,0); for (int i = 0; i < I.rows; ++i) for (int j = 0; j < I.cols; ++j) { Mat sampleMat = (Mat_<float>(1,2) << i, j); float response = svm.predict(sampleMat); if (response == 1) I.at<Vec3b>(j, i) = green; else if (response == 2) I.at<Vec3b>(j, i) = blue; } //----------------------- 5. Show the training data -------------------------------------------- int thick = -1; int lineType = 8; float px, py; // Class 1 for (int i = 0; i < NTRAINING_SAMPLES; ++i) { px = trainData.at<float>(i,0); py = trainData.at<float>(i,1); circle(I, Point( (int) px, (int) py ), 3, Scalar(0, 255, 0), thick, lineType); } // Class 2 for (int i = NTRAINING_SAMPLES; i <2*NTRAINING_SAMPLES; ++i) { px = trainData.at<float>(i,0); py = trainData.at<float>(i,1); circle(I, Point( (int) px, (int) py ), 3, Scalar(255, 0, 0), thick, lineType); } //------------------------- 6. Show support vectors -------------------------------------------- thick = 2; lineType = 8; int x = svm.get_support_vector_count(); for (int i = 0; i < x; ++i) { const float* v = svm.get_support_vector(i); circle( I, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thick, lineType); } imwrite("result.png", I); // save the Image imshow("SVM for Non-Linear Training Data", I); // show it to the user waitKey(0); }

解释

1. 建立训练样本

本例中的训练样本由分属于两个类别的2维点组成。 为了让程序更加吸引人，我们用均匀概率密度函数(PDF)随机生成样本.

我们将样本的生成代码分成两部分。

在第一部分我们生成两类线性可分样本

// class 1 随机样本生成
Mat trainClass = trainData.rowRange(0, nLinearSamples);
// x 坐标范围 [0, 0.4)
Mat c = trainClass.colRange(0, 1);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(0.4 * WIDTH));
// y 坐标范围 [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

// class 2 随机样本生成
trainClass = trainData.rowRange(2*NTRAINING_SAMPLES-nLinearSamples, 2*NTRAINING_SAMPLES);
// x 坐标范围 [0.6, 1]
c = trainClass.colRange(0 , 1);
rng.fill(c, RNG::UNIFORM, Scalar(0.6*WIDTH), Scalar(WIDTH));
// y 坐标范围 [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

在第二部分我们同时生成重叠分布线性不可分的两类样本.

// classes 1 ， 2 随机样本生成
trainClass = trainData.rowRange(  nLinearSamples, 2*NTRAINING_SAMPLES-nLinearSamples);
// x 坐标范围  [0.4, 0.6)
c = trainClass.colRange(0,1);
rng.fill(c, RNG::UNIFORM, Scalar(0.4*WIDTH), Scalar(0.6*WIDTH));
// y 坐标范围  [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

1. 设置SVM参数

See also

前一节 支持向量机(SVM)介绍 提到了类 CvSVMParams 中的一些参数需要在训练SVM之前设置。

CvSVMParams params;
params.svm_type    = SVM::C_SVC;
params.C              = 0.1;
params.kernel_type = SVM::LINEAR;
params.term_crit   = TermCriteria(CV_TERMCRIT_ITER, (int)1e7, 1e-6);

这里的设置和 前一节 的设置有两处不一样的地方

• CvSVM::C_SVC. 此处取值较小，目的是优化时不过分惩罚分类错误。这样做的目的是为了得到一个与直觉预期比较接近的分隔线。 您可以通过调整该参数来加深你对问题的理解。

  Note

  这里在两类之间重叠区域的点比较少，缩小 FRAC_LINEAR_SEP 会增加不可分区域的点数，此时 CvSVM::C_SVC 参数的调整对结果的影响深远。

• 算法终止条件. 最大迭代次数需要显著增加来容许非线性可分的训练数据， 这里的最大迭代设置是前一节的10的5次方倍。

1. 训练支持向量机

调用函数 CvSVM::train 来建立SVM模型。 注意训练过程可能耗时比较长，您需要多一点耐心来等待。

CvSVM svm;
svm.train(trainData, labels, Mat(), Mat(), params);

1. SVM区域分割

函数 CvSVM::predict 通过重建训练完毕的支持向量机来将输入的样本分类。 本例中我们通过该函数给向量空间着色， 即将图像中的每个像素当作卡迪尔平面上的一点，每一点的着色取决于SVM对该点的分类类别：深绿色表示分类为1的点，深蓝色表示分类为2的点。

Vec3b green(0,100,0), blue (100,0,0);
for (int i = 0; i < I.rows; ++i)
     for (int j = 0; j < I.cols; ++j)
     {
          Mat sampleMat = (Mat_<float>(1,2) << i, j);
          float response = svm.predict(sampleMat);

          if      (response == 1)    I.at<Vec3b>(j, i)  = green;
          else if (response == 2)    I.at<Vec3b>(j, i)  = blue;
     }

1. 显示训练样本

函数 circle 被用来显示训练样本。 标记为1的样本用浅绿表示，标记为2的样本用浅蓝表示。

int thick = -1;
int lineType = 8;
float px, py;
// Class 1
for (int i = 0; i < NTRAINING_SAMPLES; ++i)
{
     px = trainData.at<float>(i,0);
     py = trainData.at<float>(i,1);
     circle(I, Point( (int) px,  (int) py ), 3, Scalar(0, 255, 0), thick, lineType);
}
// Class 2
for (int i = NTRAINING_SAMPLES; i <2*NTRAINING_SAMPLES; ++i)
{
     px = trainData.at<float>(i,0);
     py = trainData.at<float>(i,1);
     circle(I, Point( (int) px, (int) py ), 3, Scalar(255, 0, 0), thick, lineType);
}

1. 支持向量

这里用了几个函数来获取支持向量的信息。 函数 CvSVM::get_support_vector_count 输出支持向量的数量，函数CvSVM::get_support_vector 根据输入支持向量的索引来获取指定位置的支持向量。 通过这一方法我们找到训练样本的支持向量并突出显示它们。

thick = 2;
lineType  = 8;
int x     = svm.get_support_vector_count();

for (int i = 0; i < x; ++i)
{
     const float* v = svm.get_support_vector(i);
     circle(     I,  Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thick, lineType);
}

结果

• 程序创建了一张图像，在其中显示了训练样本，其中一个类显示为浅绿色圆圈，另一个类显示为浅蓝色圆圈。
• 训练得到SVM，并将图像的每一个像素分类。 分类的结果将图像分为蓝绿两部分，中间线就是最优分割超平面。由于样本非线性可分， 自然就有一些被错分类的样本。 一些绿色点被划分到蓝色区域， 一些蓝色点被划分到绿色区域。
• 最后支持向量通过灰色边框加重显示。

你可以在 YouTube 观看本程序的实时运行.

翻译者

niesu@ OpenCV中文网站 <sisongasg@hotmail.com>

from: http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/ml/non_linear_svms/non_linear_svms.html#nonlinearsvms