背包问题(dp基础)

　　

题目描述：

　　在N件物品取出若干件放在容量为W的背包里，每件物品的体积为W1，W2……Wn（Wi为整数），与之相对应的价值为P1,P2……Pn（Pi为整数）。求背包能够容纳的最大价值。

Input

第1行，2个整数，N和W中间用空格隔开。N为物品的数量，W为背包的容量。(1 <= N <= 100，1 <= W <= 10000)
第2 - N + 1行，每行2个整数，Wi和Pi，分别是物品的体积和物品的价值。(1 <= Wi, Pi <= 10000)

Output

输出可以容纳的最大价值。

Input示例

3 6
2 5
3 8
4 9

Output示例

14

思路：设bp[i][v]为前i个物品放入到容量为v的背包当中；
　　　　状态转移方程为：

      

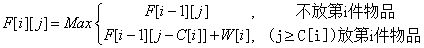
    for(int i=1;i<=n;i++){
        for(int v=1;v<=w;v++){
            if(v<W[i]) bp[i][v]=bp[i-1][v];
            else bp[i][v]=max(bp[i-1][v],bp[i-1][v-W[i]]+P[i]);
            //cout<<i<<"  "<<v<<"  "<<bp[i][v]<<endl;
        }
    }
优化：使用一位数组进行优化；将算法复杂度优化到O(n);
　　for(int i=w;i>=W[i];i--)
　　　　dp[i]=max(dp[i],dp[i-W[i]]+P[i]);