南阳OJ 61 传纸条（一）

传纸条（一）

时间限制：2000 ms  |  内存限制：65535 KB

难度：5

 

描述

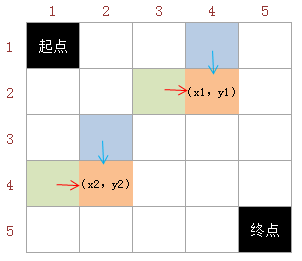
小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个m行n列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用0表示），可以用一个0-1000的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

 

输入

第一行输入N(0<N<100)表示待测数据组数。
每组测试数据输入的第一行有2个用空格隔开的整数m和n，表示班里有m行n列（2<=m,n<=50）。 
接下来的m行是一个m*n的矩阵，矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度（不大于1000）。每行的n个整数之间用空格隔开。

输出

每组测试数据输出共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。 

样例输入

1
3 3
0 3 9
2 8 5
5 7 0

样例输出

34

题目解析：

　　本道题需用到的算法为动态规划。

　　题目中提到在 m 行 n 列且带有权值的矩阵中从（1，1）到（m，n）找一条路径，然后再从（m，n）到（1,1）找一条路径，这两天路径不能重复，即每个点只能两个人只能走一次，且不可以回退，即第一条只能向下或向右，第二条只能向上或向左。化简后可知：其实就是从（1，1）到（m，n）找两条路径，这两条路径只能向下或向右且不相交，计算出这两条路径的权值和的最大值即可。

　　所以很容易构想出动态规划方程：

　　两个人走，利用四维的数组 dp[x1][y1][x2][y2] 来保存路径中间过程的权值之和的最大值，其中 x1 y1 x2 y2 分别表示两个人的位置。

　　每个人现在的位置都有两种可能：从他的上边或左边；两个人组合就有四种可能，因此：构造出动态规划方程（map[x][y] 表示权值，即好心程度）：

dp[x1][y1][x2][y2]=max(dp[x1-1][y1][x2-1][y2],dp[x1][y1-1][x2-1][y2],dp[x1][y1-1][x2][y2-1],dp[x1-1][y1][x2][y2-1])+map[x1][y1]+map[x2][y2];

　　其中 x1，x2 的取值范围为从起点到终点，即 1 ~ m，y1，y2 的取值范围为起点到终点，即 1 ~ n。

　　此方程的时间复杂度为 O(n⁴)。因此可以进一步优化：

　　假如现在是 5 x 5 的矩阵，每个人从起点走三步，会出现四种情况。

　　这四种情况的坐标分别为：（0，3）（1，2） （2，1） （3，0）。通过这四个坐标，发现一个规律： 0 + 3 = 1 + 2 = 2 + 1 = 3 + 0 = 3 = k （k为走的步数）。所有，x1 + x2 = k ， x2 + y2 = k。所以，y = k - x。因此，三维的动态规划方程为：

dp[k][x1][x2] = max(dp[k-1][x1][x2], dp[k-1][x1-1][x2-1], dp[k-1][x1-1][x2], dp[k-1][x1][x2-1]) + map[x1][k-x1] + map[x2][k-x2];

　　其中，dp[k][x1][x2] 就是四维的 dp[x1][y1][x2][y2]，dp[k-1][x1][x2] 就是四维的 dp[x1][y1-1][x2][y2-1]，map[x1][k-x1] 就是四维的 dp[x1][y1]，以此类推。

　　终点的坐标为 （m-1，n-1），但是 k 不能到达终点这个位置，因为违背了题目中两个人不能重复，k 的最大情况为（m-1）+（n-1）- 1，k 在最小情况也就是 2 x 2 的矩阵中取得最小值 1，所以 k 的取值范围为 1 ~  m+n-3。x1 和 x2 的取值范围都为从起点（0，0）到最大步数 k，即 0 ~ k。

　　此方程的时间复杂度为 O(n³)。因此还可以进一步优化：

　　从三维的动态规划方程可以发现，前一步总是 k - 1，所以，二维的动态规划方程可以优化为：

dp[x1][x2] = max(dp[x1][x2], dp[x1 - 1][x2 - 1], dp[x1 - 1][x2], dp[x1][x2 - 1]) + map[x1][k - x1] + map[x2][k - x2];

　　根据三维时的分析，两条路径都走不到终点，所以让第一个人走到终点的上方，第二个人走到终点的左方，k 的取值范围为 1 ~ （m-1）+（n-1）- 1，最终要输出的结果为 dp[m-2][m-1]。

　　此方程的时间复杂度为 O(n²)。

 

示例代码1 [四维数组]：

 注意：运用四维数组提交后报错【TimeLimitExceeded】

 #include <iostream>
 #include<stdio.h>
 #include<cmath>
 using namespace std;

 #define MAX_NUM 52

 int map[MAX_NUM][MAX_NUM];     //好心程度 | 权值
 int dp[MAX_NUM][MAX_NUM][MAX_NUM][MAX_NUM];

 int maxPath(int m, int n)
 {
     for (int x1 = ; x1 <= m; x1++)
     {
         for (int y1 = ; y1 <= n; y1++)
         {
             for (int x2 = ; x2 <= m; x2++)
             {
                 for (int y2 = ; y2 <= n; y2++)
                 {
                     /*
                         如果第一个人没有走到最后一行或最后一列，并且两个人没有重复
                         因为走到最后一行或最后一列，容易造成第二个人无路可走的情况
                     */
                     if ((x1 < m || y1 < n) && x1 == x2 && y1 == y2)
                     {
                         continue;
                     }
                     dp[x1][y1][x2][y2] = max( max(dp[x1-][y1][x2-][y2], dp[x1-][y1][x2][y2-]),
                                               max(dp[x1][y1-][x2-][y2], dp[x1][y1-][x2][y2-]))
                                              + map[x1][y1] + map[x2][y2];
                 }
             }
         }
     }
     return dp[m][n][m][n];
 }

 int main()
 {
     int x;
     scanf("%d", &x);
     while (x--) {
         int m, n;
         scanf("%d%d", &m, &n);

         for (int i = ;i <= m; i++)
             for (int j = ;j <= n; j++)
                 scanf("%d", &map[i][j]);

         int ans = maxPath(m, n);
         printf("%d\n", ans);
     } 

     return ;
 }

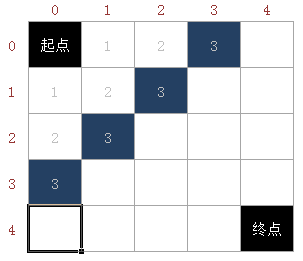
示例代码2 [三维数组]：

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 using namespace std;

 #define MAX_NUM 52

 int map[MAX_NUM][MAX_NUM];     //好心程度 | 权值
 int dp[MAX_NUM+MAX_NUM][MAX_NUM][MAX_NUM];

 int maxPath(int m, int n)
 {
     for (int k = ;k <= m+n-; k++)
     {
         for (int x1 = ; x1 <= k; x1++)
         {
             for (int x2 = ; x2 <= k; x2++)
             {
                 if (x1 == x2)    //x1 == x2 相当于(x1 == x2 && y1 = y2)
                 {
                     continue;
                 }
                 dp[k][x1][x2] = max(max(dp[k-][x1][x2], dp[k-][x1-][x2-]),
                                     max(dp[k-][x1-][x2], dp[k-][x1][x2-]))
                                 + map[x1][k-x1] + map[x2][k-x2];
             }
         }
     }
     return dp[m+n-][m-][m-];
 }

 int main()
 {
     int x;
     scanf("%d", &x);
     while (x--) {
         int m, n;
         scanf("%d%d", &m, &n);

         for (int i = ; i < m; i++)
             for (int j = ; j < n; j++)
                 scanf("%d", &map[i][j]);

         int ans = maxPath(m, n);
         printf("%d\n", ans);
     }

     return ;
 }

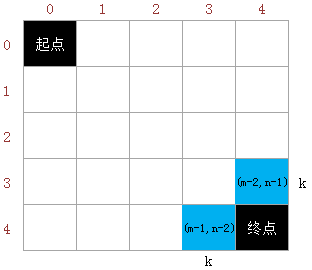
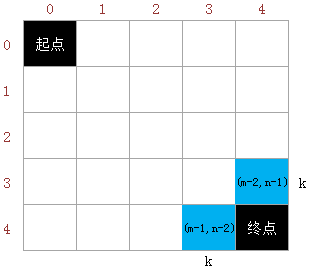
示例代码3 [二维数组]：

 #include<iostream>
 #include<cstdio>
 #include<string.h>
 #include<cmath>
 using namespace std;

 #define MAX_NUM 52

 int map[MAX_NUM][MAX_NUM];   //好心程度 | 权值
 int dp[MAX_NUM][MAX_NUM];

 int maxPath(int m, int n)
 {
     memset(dp, , sizeof(dp));
     for (int k = ; k <= m+n-; k++)
     {
         for (int x1 = m-; x1 >= ; x1--)
         {
             for (int x2 = m-; x2 > x1; x2--)
             {
                 if ( k >= x1 && k >= x2)    //x + y = k,当k >= x时，说明还在矩阵范围之内
                 {
                     dp[x1][x2] = max(max(dp[x1][x2], dp[x1-][x2-]),
                                      max(dp[x1-][x2], dp[x1][x2-]))
                                  + map[x1][k-x1] + map[x2][k-x2];
                 }
             }
         }
     }
     return dp[m-][m-];
 }

 int main()
 {
     int x;
     scanf("%d", &x);
     while (x--) {
         int m, n;
         scanf("%d %d", &m, &n);

         for (int i = ;i < m; i++)
             for (int j = ; j < n; j++)
                 scanf("%d", &map[i][j]);  

         int ans = maxPath(m, n);
         printf("%d\n", ans);
     }

     return ;
 }