Data_Structure-绪论作业

一.作业题目

　　仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
　　有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3

 

 二.作业内容

　　1.抽象数据结构描述

ADT Rational{
　　数据结构：
　　　　D={e1,e2|e1,e2为整数}
　　数据关系：
　　　　R={<e1,e2>|e1为有理数的分子，e2为有理数的分母，e2不为0}
　　基本操作：
　　　　Construct_rational_Numbers(&T,e1,e2)
　　　　//操做结果：构造有理数T，元素e1,e2分别被赋以分子、分母值
　　　　Destroy_rational_Numbers(&T)
　　　　//操做结果：销毁有理数T
　　　　Get(T,i,&e)
　　　　//操作结果：用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母
　　　　Put(&T,i,e)
　　　　//操作结果：将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
　　　　add(T1,T2,&T3)
　　　　//操作结果：有理数T1,T2相加,结果存入有理数T3
　　　　subtract(T1,T2,&T3)
　　　　//操作结果：将T1，T2相减，结果存入T3
　　　　multiply(T1,T2,&T3)
　　　　//操作结果：将T1，T2相乘，结果存入T3
　　　　division(T1,T2,&T3)
　　　　//操作结果：将T1，T2相除，结果存入T3

　　　　}ADT Rational

　　2.数据结构、函数说明

　　　　1.头文件

　　

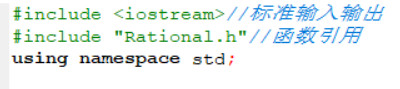
　　　　2.函数

　　

　　3.代码实现说明

　　　　1.用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母

　　　　

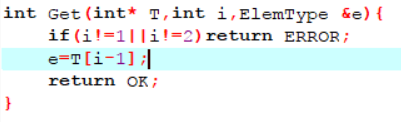
　　　　2.将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母

　　　　

　　　　3.有理数T1,T2相加,结果存入T3

　　　　

　　　　4.将T1，T2相减，结果存入T3

　　　　

　　　　5.将T1，T2相乘，结果存入T3

　　　　

　　　　6.将T1，T2相除，结果存入T3

　　　　

　　　　7.返回e1和e2的最大公约数

　　　　

　　　　8.返回T3的值

　　　　

　　4.结果展示

　　　　　1.T1<T2

　　　　　　　

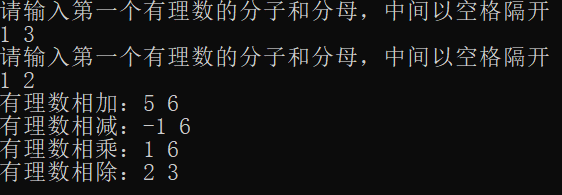
　　　　　2.T1>T2

　　　　　　

　　　　　3.T1=T2

　　　　　　

　　　　　4.T1,T2都为负数

　　　　　　

　　　　　5.分母为零

　　　　　　

　　　　　6.分子为零

　　　　　　

　　5.总结

本次作业让我初步认识到了抽象数据结构的构建和重点要素。抽象数据结构在编程的过程中，让我们更加明白程序所需要的元素和执行的操作。

数据结构是计算机存储、组织数据的方式。数据结构是相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。

抽象数据结构是不考虑计算机内部如何储存和具体算法的前提下，描述了数据的集合、数据之间的关系和操作的集合。（重点关心其的逻辑特征）