BZOJ3224_普通平衡树_KEY

题目传送门

平衡二叉树（Balanced Binary Tree）具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

平衡树是一种在信息竞赛中常用的数据结构，而Treap也是其中之一。说实话花了一天来屮这个Treap。

Treap简单地来说就是二叉搜索树的升级版，只不过在其基础上增加了一个rand值，并利用堆维护rand值，使二叉搜索树的rand值满足堆的性质。

从而保证Treap的高度基本为logN。

Treap的核心就是一个Rotate，它能保证Treap的性质。

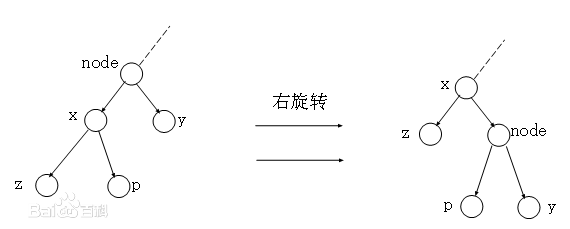
插入：像二叉搜索树一样插入，在子节点不满足堆的性质时Rotate。

删除：先找到节点，如果没有儿子，直接删除。有一个儿子，直接将儿子覆盖到当前节点。有两个儿子，Rotate之后递归向下。

其他操作较简单，看code有解释。

code：

#include <cstdio>
#include <cstdlib>
#include <cstring>

int read()
{
    char c;while(c=getchar(),(c<''||c>'')&&c!='-');
    int x=,y=;c=='-'?y=-:x=c-'';
    while(c=getchar(),c>=''&&c<='')x=x*+c-'';
    return x*y;
}

int N,dist;

struct Treap{
    int tr[][],cnt,ks[],v[],tot[];
    int f[],root;
    Treap(){
        memset(tr,,sizeof tr);
        memset(ks,,sizeof ks);
        memset(v,,sizeof v);
        cnt=;
    }

    void rotate(int &x,int o)//旋转
    {
        int k=tr[x][o];
        tr[x][o]=tr[k][o^];
        tr[k][o^]=x;
        f[k]=f[x];//更新
        f[x]=f[tr[x][]]+f[tr[x][]]+tot[x];
        x=k;
    }

    void Insert(int &x,int val)//插入节点
    {
        if(!x){
            x=++cnt;
            ks[x]=rand();
            v[x]=val;
            tot[x]=;//当前节点共有几个相同的值
            f[x]=;
            return ;
        }f[x]++;//统计当前这个节点的子树共有几个节点
        if(val==v[x]){tot[x]++;return ;}
        int to=val>v[x];
        Insert(tr[x][to],val);
        if(ks[tr[x][to]]>ks[x])rotate(x,to);//不满足堆的性质，Rotate
        return ;
    }

    void Delete(int &x,int val)//删除
    {
        if(!x)return ;
        if(val==v[x]){
            if(tot[x]>){tot[x]--;f[x]--;return ;}
            if(!tr[x][]&&!tr[x][]){v[x]=tot[x]=ks[x]=;x=;return ;}
            if(!(tr[x][]*tr[x][])){
                x=tr[x][]+tr[x][];
                return ;
            }
            rotate(x,);
            Delete(x,val);//递归向下
            return ;
        }
        int to=val>v[x];
        f[x]--;//减去总结点数
        Delete(tr[x][to],val);
　　　　 f[x]=f[tr[x][0]]+f[tr[x][1]]+tot[x];
        return ;
    }

    int QueryX(int x,int val)
    {
        if(!x)return ;
        if(v[x]==val)return f[tr[x][]]+;//小细节，可以直接return左子树总结点+1
        int to=val>v[x];
        return QueryX(tr[x][to],val)+(to?(f[tr[x][]]+tot[x]):);//如果是访问右子树retun之后要加上f[tr[x][0]]+tot[x]
　　　　 //查询X的排名
    }

    int QueryK(int x,int kth)
    {
        if(!x)return ;
        if(kth<=f[tr[x][]])return QueryK(tr[x][],kth);//在左子树
        if(kth>f[tr[x][]]+tot[x])return QueryK(tr[x][],kth-(f[tr[x][]]+tot[x]));//在右子树
        return v[x];//查询排名为X的数
    }

    int pre(int x,int val)//前驱
    {
        if(!x)return ;
        if(v[x]>=val)pre(tr[x][],val);
        else{
            dist=x;
            pre(tr[x][],val);
        }
    }

    int bac(int x,int val)//后继
    {
        if(!x)return ;
        if(v[x]<=val)bac(tr[x][],val);
        else{
            dist=x;
            bac(tr[x][],val);
        }
    }
}T;

int main()
{
    int W=('Y'+'u'+'a'+'o')*('S'+'h'+'i')*('D'+'o'+'g');
    srand(W);
    N=read();
        while(N--){
            int o=read(),x=read();
            switch(o){
                case :T.Insert(T.root,x);break;
                case :T.Delete(T.root,x);break;
                case :printf("%d\n",T.QueryX(T.root,x));break;
                case :printf("%d\n",T.QueryK(T.root,x));break;
                case :dist=,T.pre(T.root,x),printf("%d\n",T.v[dist]);break;
                case :dist=,T.bac(T.root,x),printf("%d\n",T.v[dist]);break;
            }
        }
}