[HNOI2007][BZOJ1185] 最小矩形覆盖 [凸包+旋转卡壳]

题面

BZOJ题面

前置芝士

建议先学习向量相关的计算几何基础

计算几何基础戳这里

思路

用这道题学习一下凸包和旋转卡壳

首先是凸包部分

凸包

求凸包用的算法是graham算法

算法流程如下：

找到$y$坐标最小的一点作为原点

对原点之外的所有点按照到原点的极角排序（这里因为选取了最靠下的，所以极角范围在$[0,\pi]$）

依次遍历所有排序后的点，加入一个单调栈中：每次判断（栈顶元素和栈顶第二元素之间的斜率）是否大于（当前点和栈顶第二元素之间的斜率）

注意一旦这个大于成立了，栈顶元素就会在当前元素和栈顶第二元素的连线的“下面”，也就是在凸包里面了

因为我们事先按照极角排序了，所以这一单调栈可以不重复不遗漏地记录凸包上所有点

注意这样求出来的凸包上的点是逆时针排序的（根本原因是因为极角排序就是逆时针绕圈）

graham算法的复杂度是$O(n\log n)$，瓶颈是排序

旋转卡壳

首先，我在这道题里面用的不是标准的旋转卡壳算法......但是也是“旋转+卡壳”的思路

标准版的旋转卡壳戳这里，这里标准版指的是用4条边去卡壳，我写的是一条边和3个极值点

对于最小面积矩形，我们有结论：这一外接矩形一定有一条边和凸包的一条边重合

注意这个结论对于最小周长矩形依然成立

证明嘛......我愣是没找到。感性理解一下就是对于一个四边都接在凸包端点上的矩形，把它旋转一下一定更优

核心算法流程如下：

我们遍历凸包上的每一条边，并对于每一条边求出以这条边为x轴时，最靠左的点、最靠右的点、最靠上的点

设求出来的凸包上的点是$q[0...m-1]$

假设我们当前的边的两个端点是凸包上的$q[i],q[i+1]$，而且是有向的（i指向i+1），那么上述三个端点有如下性质：

对于最靠左的点$q[l]$，$vec(q[i],q[l])\ast vec(q[i],q[i+1])$是所有$l$中最小的

对于最靠右的点$q[r]$，$vec(q[i],q[r])\ast vec(q[i],q[i+1])$是所有$r$中最大的

对于最靠上的点$q[u]$，$vec(q[i],q[i+1])$叉乘$vec(q[i],q[u])$是所有$u$中最大的

其中$vec(u,v)$表示从点$u$指向$v$的向量

前两个的证明，利用点乘的性质：因为点乘的被投影向量长度相等，所以决定点乘结果大小的就是投影的大小

那么显然投影最小最靠左，投影最大最靠右

第三个的证明，利用叉乘的性质：叉乘等于两个向量逆时针旋转构成的有向平行四边形面积

因为平行四边形底边长度相同，而且$vec(q[i],q[i+1])$一定在所有从$q[i]$出发的向量的顺时针方向，所以反过来旋转一定是正的，叉乘最大就是最高

图示如下：

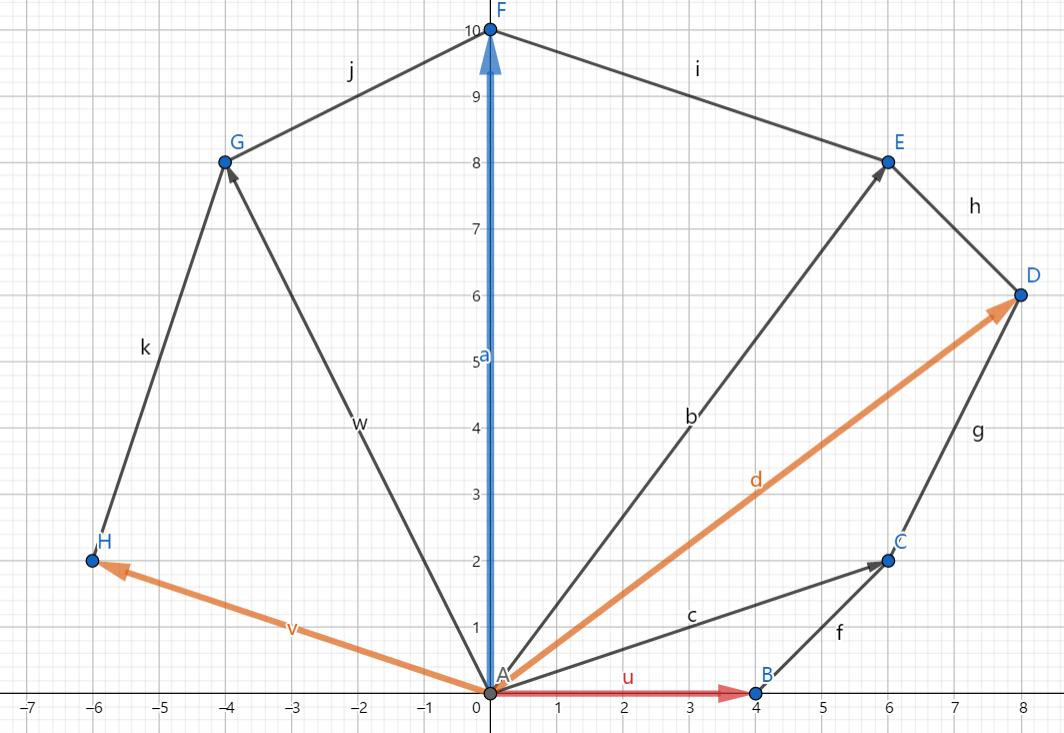
知道了这三个点以后，我们就可以知道这个矩形的长宽，进而求出面积了

又有性质：我们每次从$vec(q[i],q[i+1])$旋转到$vec(q[i+1],q[i+2])$的时候，$l,r,u$也会跟着逆时针旋转，所以只要枚举即可

这样，整个旋转卡壳就是“遍历所有边”+“顺序求出端点”的过程，总复杂度是$O(n)$的

Code

代码中node是向量结构体，对于点我们用位矢表示，也是向量

标$\ast$的是叉乘，标\的是点乘

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cassert>
#include<cmath>
#define eps 1e-9
#define ll long long
using namespace std;
inline int read(){
	int re=0,flag=1;char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-') flag=-1;
		ch=getchar();
	}
	while(isdigit(ch)) re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
	return re*flag;
}
struct node{
	double x,y;
	node(double xx=0.0,double yy=0.0){x=xx;y=yy;}
	inline bool operator <(const node &b){return ((fabs(y-b.y)<eps)?(x<b.x):(y<b.y));}
	inline friend bool operator ==(const node &a,const node &b){return ((fabs(a.x-b.x)<eps)&&(fabs(a.y-b.y)<eps));}
	inline friend bool operator !=(const node &a,const node &b){return !(a==b);}
	inline friend node operator +(const node &l,const node &r){return node(l.x+r.x,l.y+r.y);}
	inline friend node operator -(const node &l,const node &r){return node(l.x-r.x,l.y-r.y);}
	inline friend node operator *(node l,double r){return node(l.x*r,l.y*r);}
	inline friend double operator *(const node &l,const node &r){return l.x*r.y-l.y*r.x;}
	inline friend double operator /(const node &l,const node &r){return l.x*r.x+l.y*r.y;}
	inline friend double dis(const node &a){return sqrt(a.x*a.x+a.y*a.y);}
}a[100010],q[100010],x[10];
int n,top;double ans=1e60;
inline bool cmp(node l,node r){
	double tmp=(a[1]-l)*(a[1]-r);
	if(fabs(tmp)<eps) return dis(a[1]-l)<dis(a[1]-r);
	else return tmp>0;
}
void graham(){//get a counter-clockwise convex
	int i;
	for(i=2;i<=n;i++){
		if(a[i]<a[1]) swap(a[1],a[i]);
	}
	sort(a+2,a+n+1,cmp);
	q[++top]=a[1];
	q[++top]=a[2];
	for(i=3;i<=n;i++){
		while(top>1&&((q[top]-q[top-1])*(a[i]-q[top])<eps)) top--;
		q[++top]=a[i];
	}
	q[0]=q[top];
}
void RC(){//RotatingCalipers
	int l=1,r=1,p=1,i;
	double L,R,D,H,tmp;
	for(i=0;i<top;i++){
		D=dis(q[i]-q[i+1]);
		while((q[i+1]-q[i])*(q[p+1]-q[i])-(q[i+1]-q[i])*(q[p]-q[i])>-eps) p=(p+1)%top;
		while((q[i+1]-q[i])/(q[r+1]-q[i])-(q[i+1]-q[i])/(q[r]-q[i])>-eps) r=(r+1)%top;
		if(i==0) l=r;
		while((q[i+1]-q[i])/(q[l+1]-q[i])-(q[i+1]-q[i])/(q[l]-q[i])<eps) l=(l+1)%top;
		L=(q[i+1]-q[i])/(q[l]-q[i])/D;
		R=(q[i+1]-q[i])/(q[r]-q[i])/D;
		H=(q[i+1]-q[i])*(q[p]-q[i])/D;
		tmp=(R-L)*H;
		if(tmp<ans){
			ans=tmp;
			x[0]=q[i]+(q[i+1]-q[i])*(R/D);
			x[1]=x[0]+(q[r]-x[0])*(H/dis(x[0]-q[r]));
			x[2]=x[1]-(x[0]-q[i])*((R-L)/dis(q[i]-x[0]));
			x[3]=x[2]-(x[1]-x[0]);
		}
	}
}
int main(){
	n=read();int i,j;
	for(i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
	graham();
	RC();
	printf("%.5lf\n",ans);
	j=0;
	for(i=1;i<4;i++) if(x[i]<x[j]) j=i;
	for(i=0;i<4;i++) printf("%.5lf %.5lf\n",x[j].x,x[j].y),j=(j+1)%4;
}