LightOJ 1203--Guarding Bananas(二维凸包+内角计算)

1203 - Guarding Bananas

PDF (English)

Statistics

Forum

Time Limit: 3 second(s)

Memory Limit: 32 MB

Once there was a lazy monkey in a forest. But he loved banana too much. One day there was a storm in the jungle and all the bananas fell from the trees. The monkey didn't want to lose any of the bananas. So, he wanted to find a banana such that he can eat that and he can also look after the other bananas. As he was lazy, he didn't want to move his eyes too wide. So, you have to help him finding the banana from where he can look after all the bananas but the degree of rotating his eyes is as small as possible. You can assume that the position of the bananas can be modeled as 2D points.

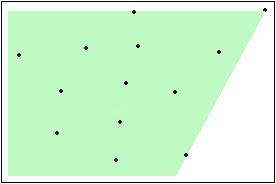
Here a banana is shown, from where the monkey can look after all the bananas with minimum eye rotation.

Input

Input starts with an integer T (≤ 13), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 10⁵) denoting the number of bananas. Each of the next n lines contains two integers x y (-10⁹ ≤ x, y ≤ 10⁹) denoting the co-ordinate of a banana. There can me more than one bananas in the same co-ordinate.

Output

For each case, print the case number and the minimum angle in degrees. Errors less than 10^-6 will be ignored.

Sample Input	Output for Sample Input
2 1 4 4 4 0 0 10 0 10 10 2 1	Case 1: 0 Case 2: 45.0000000

Note

Dataset is huge. Use faster I/O methods.

• 题意：在所有给定的香蕉中找到一个香蕉，使得从这个香蕉看向其他香蕉的角度尽可能小的同时看到的香蕉数目尽可能多。
• 由于香蕉可以化为半径忽略不计的二维平面上的点，所以可以想到，站在这些点的凸包的顶点处看过去的角度小并且看到的点更多，否则，总可以向这些定顶点处移动，使得看到的点更多或者角度更小。
• 所以这道题就是求其凸包，然后找到里面最小的那个内角。

•  #include<iostream>
   #include<algorithm>
   #include<cmath>
   #include<cstdio>
   #include<cstring>
   using namespace std;
   const int maxn = 1e5 + ;
   const double pi = acos(-1.0);
   const double eps = 1e-;
   int sgn(double x) {
       if (fabs(x) < eps)return ;
       if (x < )return -;
       else return ;
   }
   typedef struct point {
       double x, y;
       point() {
  
       }
       point(double a, double b) {
           x = a;
           y = b;
       }
       point operator -(const point &b) const {
           return point(x - b.x, y - b.y);
       }
       double operator *(const point &b)const {
           return x*b.x + y*b.y;
       }
       double operator ^(const point &b)const {    //叉乘
           return x*b.y - y*b.x;
       }
       bool operator <(point b)const {
           return sgn(x - b.x) ==  ? sgn(y - b.y)< : x<b.x;
       }
       //返回pa,pb的夹角，该点看a,b的夹角,弧度制
       //弧度＝度×π/180°
       //度＝弧度×180°/π
       double rad(point a, point b) {
           point p = *this;
           return fabs(atan2(fabs((a - p) ^ (b - p)), (a - p)*(b - p)));
       }
   }point;
   point p[maxn];
   int n = , res[maxn];
   int top;//top模拟栈顶
   bool multi(point p1, point p2, point p0) {  //判断p1p0和p2p0的关系，<0,p1p0在p2p0的逆时针方向,>0,p1p0在p2p0的顺时针方向
       return (p1.x - p0.x)*(p2.y - p0.y) >= (p2.x - p0.x)*(p1.y - p0.y);
   }
   double Graham() {
       int i, len;//top模拟栈顶
       sort(p, p + n);
       top = ;
       //少于3个点也就没有办法形成凸包
       if (n == )return ; res[] = ;
       if (n == )return ; res[] = ;
       if (n == )return ; res[] = ;
       for (i = ; i < n; i++) {
           while (top&&multi(p[i], p[res[top]], p[res[top - ]]))    //如果当前这个点和栈顶两个点构成折线右拐了，就回溯到上一个点
               top--;                                                //弹出栈顶
           res[++top] = i;                                           //否则将这个点入栈
       }
       len = top;
       res[++top] = n - ;
       for (i = n - ; i >= ; i--) {
           while (top != len&&multi(p[i], p[res[top]], p[res[top - ]]))
               top--;
           res[++top] = i;
       }
       double ans =0x3f3f3f;
       res[top] = res[],res[top + ] = res[];
       for (int i = ; i <= top; i++) {
           ans = min(ans, p[res[i]].rad(p[res[i + ]], p[res[i - ]]));
       }
       return ans / pi * ;
   }
   inline int read()
   {
       int x = , f = ; char ch = getchar();
       while (ch<'' || ch>'') { if (ch == '-')f = -; ch = getchar(); }
       while (ch >= ''&&ch <= '') { x = x *  + ch - ''; ch = getchar(); }
       return x*f;
   }
   int main(void) {
       int t;
       t = read();
       for (int cnt = ; cnt <= t; cnt++) {
           cin >> n;
           for (int i = ; i < n; i++) {
               p[i].x = read();
               p[i].y = read();
           }
           printf("Case %d: ", cnt);
           printf("%.7lf\n", Graham());
       }
       return ;
   }