[WikiOI "天梯"1281] Xn数列
题目描述Description
给你6个数,m, a, c, x0, n, g
Xn+1 = ( aXn + c ) mod m,求Xn
m, a, c, x0, n, g<=10^18
输入描述Input Description
一行六个数 m, a, c, x0, n, g
输出描述Output Description
输出一个数 Xn mod g
样例输入Sample Input
11 8 7 1 5 3
样例输出Sample Output
2
数据范围及提示Data Size & Hint
int64按位相乘可以不要用高精度。
题目分析
典型的矩阵快速幂问题。由递推式 Xn+1 = ( aXn + c ) mod m 可以构造出矩阵方程:
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
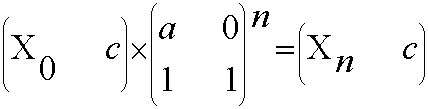
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = ;
while(b)
{
if(b & )ans = (ans + a)% m;
a = (a << )% m;
b >>= ;
}
return ans;
}
struct Matrix2
{
LL val[][];
Matrix2(LL k1,LL k2,LL k3,LL k4)
{
val[][] = k1; val[][] = k2; val[][] = k3; val[][] = k4;
}
void Mlti(Matrix2 &m) //矩阵乘法
{
LL v1 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v2 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v3 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v4 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
val[][] = v1,val[][] = v2,val[][] = v3,val[][] = v4;
}
};
int main()
{
ios::sync_with_stdio(); //感谢陈思学长!
cin >>m >>a >>c >>x0 >>n >>MOD;
Matrix2 M(a, , , );
Matrix2 ans = M;
n -= ;
while(n)
{
if(n & ) ans.Mlti(M);
M.Mlti(M);
n >>=;
}
cout << ((mlti(x0, ans.val[][])+mlti(c, ans.val[][]))%m)%MOD;
return ;
}
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
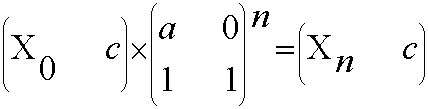
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = ;
while(b)
{
if(b & )ans = (ans + a)% m;
a = (a << )% m;
b >>= ;
}
return ans;
}
struct Matrix2
{
LL val[][];
Matrix2(LL k1,LL k2,LL k3,LL k4)
{
val[][] = k1; val[][] = k2; val[][] = k3; val[][] = k4;
}
void Mlti(Matrix2 &m) //矩阵乘法
{
LL v1 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v2 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v3 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v4 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
val[][] = v1,val[][] = v2,val[][] = v3,val[][] = v4;
}
};
int main()
{
ios::sync_with_stdio(); //感谢陈思学长!
cin >>m >>a >>c >>x0 >>n >>MOD;
Matrix2 M(a, , , );
Matrix2 ans = M;
n -= ;
while(n)
{
if(n & ) ans.Mlti(M);
M.Mlti(M);
n >>=;
}
cout << ((mlti(x0, ans.val[][])+mlti(c, ans.val[][]))%m)%MOD;
return ;
}
[WikiOI "天梯"1281] Xn数列的更多相关文章
- 【wikioi】1281 Xn数列(矩阵乘法)
http://wikioi.com/problem/1281/ 矩阵真是个神奇的东西.. 只要搞出一个矩阵乘法,那么递推式可以完美的用上快速幂,然后使复杂度降到log 真是神奇. 在本题中,应该很快能 ...
- Codevs No.1281 Xn数列
2016-06-01 16:28:25 题目链接: Xn数列 (Codevs No.1281) 题目大意: 给定一种递推式为 Xn=(A*Xn-1+C)%M 的数列,求特定的某一项%G 解法: 矩阵乘 ...
- codevs 1281 Xn数列
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
- 【CODEVS】1281 Xn数列
[算法]矩阵快速幂 [题解]T*A(n-1)=A(n)矩阵如下: a 1 * x(n-1) 0 = xn 0 0 1 c 0 c 0 防止溢出可以用类似快速幂的快速乘. ...
- codevs 1281 Xn数列 (矩阵乘法)
/* 再来个题练练手 scanf longlong 有bug....... */ #include<cstdio> #include<iostream> #include< ...
- C++之路进阶——codevs1281(Xn数列)
1281 Xn数列 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 大师 Master 题目描述 Description 给你6个数,m, a, c, x0, n, ...
- Xn数列(codevs 1281)
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
- 【wikioi】1250 Fibonacci数列(矩阵乘法)
http://wikioi.com/problem/1250/ 我就不说这题有多水了. 0 1 1 1 矩阵快速幂 #include <cstdio> #include <cstri ...
- codevs1281 Xn数列
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
随机推荐
- Python第三方库matplotlib(2D绘图库)入门与进阶
Matplotlib 一 简介: 二 相关文档: 三 入门与进阶案例 1- 简单图形绘制 2- figure的简单使用 3- 设置坐标轴 4- 设置legend图例 5- 添加注解和绘制点以及在图形上 ...
- nmap导出处理脚本
import sys log = open("result.gnmap","r") xls = open("output.csv",&quo ...
- Python3 PyPAML 模块(配置文件的操作)
YAML 是专门用来写配置文件的语言,非常简洁和强大 它的基本语法规则如下: 1.大小写敏感 2.使用缩进表示层级关系 3.缩进时不允许使用Tab键,只允许使用空格. 4.缩进的空格数目不重要,只要相 ...
- 如何才可以干掉Cortana进程,开机不启动
直接禁用即可WIN——设置——隐私——语音.墨迹书写和键入——停止收集有关我的信息——关闭
- python并发模块之concurrent.futures(二)
python并发模块之concurrent.futures(二) 上次我们简单的了解下,模块的一些基本方法和用法,这里我们进一步对concurrent.futures做一个了解和拓展.上次的内容点这. ...
- memcached和redis区别
Memcached:是高性能分布式内存缓存服务器,本质是一个内存 key-value 数据库,但不支持数据持久化,服务器关闭后,数据全丢失.只支持 key-value 结构. Redis:将大部分数据 ...
- Mac 使用自带的Ruby 安装brew
Homebrew简称brew,OSX上的软件包管理工具,在Mac终端可以通过brew安装.更新.卸载软件. 首先要安装brew,在 mac 中使用finder 搜索 终端(terminal)打开命令行 ...
- python 作业
Linux day01 计算机硬件知识整理 作业要求:整理博客,内容如下 编程语言的作用及与操作系统和硬件的关系 应用程序->操作系统->硬件 cpu->内存->磁盘 cpu与 ...
- poj 2251(同余)
Ones Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 11461 Accepted: 6488 Description ...
- QT 中怎样使得控件与 界面等比例变化
转自:https://github.com/exoticknight/blog-post/blob/master/python-with-Qt-application-development/pyth ...
