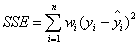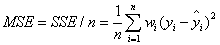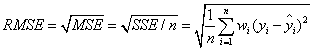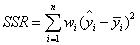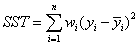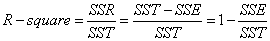SSE(和方差、误差平方和)：The sum of squares due to error

MSE(均方差、方差)：Mean squared error
RMSE(均方根、标准差)：Root mean squared error
R-square(确定系数)：Coefficient of determination
Adjusted R-square：Degree-of-freedom adjusted coefficient of determination

下面我对以上几个名词进行详细的解释下，相信能给大家带来一定的帮助！！

一、SSE(和方差)

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗，所以效果一样

二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值，也就是SSE/n，和SSE没有太大的区别，计算公式如下

三、RMSE(均方根)
该统计参数，也叫回归系统的拟合标准差，是MSE的平方根，就算公式如下

在这之前，我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!

四、R-square(确定系数)
在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的
(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下

细心的网友会发现，SST=SSE+SSR，呵呵只是一个有趣的问题。而我们的“确定系数”是定义为SSR和SST的比值，故

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好

转自：https://blog.csdn.net/ac540101928/article/details/75388823

SSE,MSE,RMSE,R-square 指标讲解的更多相关文章

  1. SSE,MSE,RMSE,R-square指标讲解

    SSE(和方差.误差平方和):The sum of squares due to errorMSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...

  2. Data Mining： SSE,MSE,RMSE,R-square指标讲解

    转载自:http://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差.误差平方和):The sum of squares due ...

  3. 衡量线性回归法的指标MSE, RMSE,MAE和R Square

    衡量线性回归法的指标:MSE, RMSE和MAE 举个栗子: 对于简单线性回归,目标是找到a,b 使得尽可能小 其实相当于是对训练数据集而言的,即 当我们找到a,b后,对于测试数据集而言 ,理所当然, ...

  4. 【笔记】衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square

    衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square 衡量线性回归法的指标 对于分类问题来说,我们将原始数据分成了训练数据集和测试数据集两部分,我们使用训练数据集得到模型以后 ...

  5. 线性回归中常见的一些统计学术语（RSE RSS TSS ESS MSE RMSE R2 Pearson's r）

    TSS: Total Sum of Squares(总离差平方和) --- 因变量的方差 RSS: Residual Sum of Squares (残差平方和) ---  由误差导致的真实值和估计值 ...

  6. MSE,RMSE

    MSE: Mean Squared Error 均方误差是指参数估计值与参数真值之差平方的期望值; MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度. RMSE  ...

  7. 回归评价指标MSE、RMSE、MAE、R-Squared

    分类问题的评价指标是准确率,那么回归算法的评价指标就是MSE,RMSE,MAE.R-Squared. MSE和MAE适用于误差相对明显的时候,大的误差也有比较高的权重,RMSE则是针对误差不是很明显的 ...

  8. 机器学习|线性回归三大评价指标实现『MAE, MSE, MAPE』（Python语言描述）

    原文地址 ?传送门 对于回归预测结果,通常会有平均绝对误差.平均绝对百分比误差.均方误差等多个指标进行评价.这里,我们先介绍最常用的3个: 平均绝对误差(MAE) 就是绝对误差的平均值,它的计算公式如 ...

  9. SSE技术详解：一种全新的HTML5服务器推送事件技术

    前言 一般来说,Web端即时通讯技术因受限于浏览器的设计限制,一直以来实现起来并不容易,主流的Web端即时通讯方案大致有4种:传统Ajax短轮询.Comet技术.WebSocket技术.SSE(Ser ...

随机推荐

  1. C - 壮志难酬

    #include<stdio.h> #include<stdlib.h> #include<string.h> int main() { ]= {'}; int i ...

  2. PHP stream 学习笔记一(同步阻塞 IO 模型)

    原文http://blog.csdn.net/shagoo/article/details/6396089 [root@localhost php]# vi server_one.php <?p ...

  3. CDOJ 1281 暴兵的卿学姐 构造题

    暴兵的卿学姐 题目连接: http://acm.uestc.edu.cn/#/problem/show/1281 Description 沈宝宝又和卿学姐开始玩SC2了! 自从沈宝宝学会新的阵型后,就 ...

  4. linux shell 自定义函数(定义、返回值、变量作用域）介绍

    linux shell 可以用户定义函数,然后在shell脚本中可以随便调用.下面说说它的定义方法,以及调用需要注意那些事项. 一.定义shell函数(define function) 语法: [ f ...

  5. php-scandir()报错

    l       linux下 vim /usr/local/php/etc/php.in l       直接斜杠找 /disable_functions   回车 l       按i键 l     ...

  6. WPF中的动画——（五）关键帧动画

    与 From/To/By 动画类似,关键帧动画以也可以以动画形式显示目标属性值. 和From/To/By 动画不同的是, From/To/By 动画只能控制在两个状态之间变化,而关键帧动画则可以在多个 ...

  7. HDU 4642 Fliping game (2013多校4 1011 简单博弈)

    Fliping game Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)Tota ...

  8. Windows7下安装与破解IntelliJ IDEA2017(转载)

    IDEA 全称 IntelliJ IDEA,是Java语言开发的集成环境,IntelliJ在业界被公认为最好的java开发工具之一,尤其在智能代码助手.代码自动提示.重构.J2EE支持.各类版本工具( ...

  9. onmouseout,mouseover经过子元素也触发的问题解决方案

    在mouseout与mouseover的冒泡问题上,相信有很多朋友都遇到过.今天这里就总结一下 关于mouseover和mouseout冒泡问题的解决方案: 首先,看下event.relatedTar ...

  10. javascript 中用到的时间戳函数

    JavaScript 获取当前时间戳:第一种方法: var timestamp = Date.parse(new Date()); 例如结果:1280977330000第二种方法: var times ...