最短路径-迪杰斯特拉(dijkstra)算法及优化详解

简介：

dijkstra算法解决图论中源点到任意一点的最短路径。

算法思想：

算法特点：

　　dijkstra算法解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

算法的思路

　　dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。 
然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点， 
然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。 
然后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

图解：

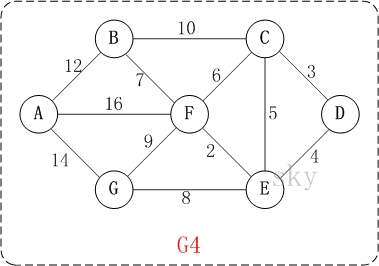
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。以下B节点中23应为13。

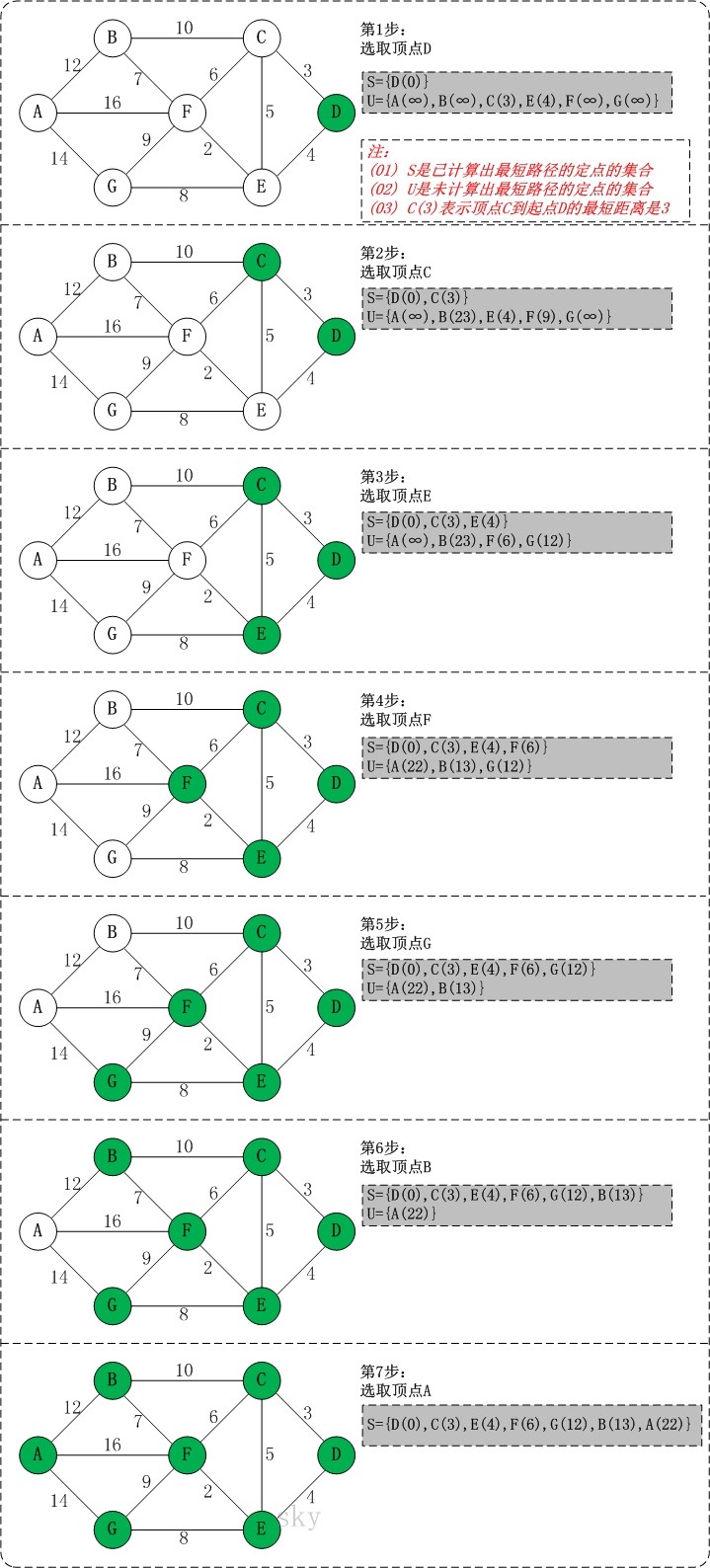
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。 
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。 
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。 
此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。 
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。 
此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。 
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

代码：

邻接矩阵：

#include<stdio.h>
#include<string.h>
#define inf 0x3f3f3f3f
][],dis[],visit[];
/*
关于三个数组：map数组存的为点边的信息，比如map[1][2]=3，表示1号点和2号点的距离为3
dis数组存的为起始点与每个点的最短距离，比如dis[3]=5，表示起始点与3号点最短距离为5
visit数组存的为0或者1，1表示已经走过这个点。
*/
int n,m;
int dijstra()
{
    ,min,sum=;
    memset(visit,,sizeof(visit));//初始化为.，表示开始都没走过
    ; i<=n; ++i)
    {
        dis[i]=map[][i];
    }
    visit[]=;
    dis[]=;
    ; i<n; i++)
    {
        min=inf;
        ; j<=n; ++j)
        {
            &&min>dis[j])
            {
                min=dis[j];
                pos=j;
            }
        }
        visit[pos]=;//表示这个点已经走过
        ; j<=n; ++j)
        {
            &&dis[j]>dis[pos]+map[pos][j])//更新dis的值
                dis[j]=dis[pos]+map[pos][j];
        }
    }
    return dis[n];
}
int main()
{
    int i,j;
    while(~scanf("%d%d",&n,&m),n||m)//n表示n个点，m表示m条边
    {
        ; i<=n; ++i)
        {
            ; j<=n; ++j)
            {
                map[i][j]=inf;//开始时将每条边赋为最大值
            }
        }
        int a,b,c;
        ; i<=m; ++i)
        {
            scanf("%d%d%d",&a,&b,&c);
            if(c<map[a][b])//防止有重边
                map[a][b]=map[b][a]=c;
        }
        int count=dijstra();
        printf("%d\n",count);
    }
    ;
}

优先队列优化：

+;
struct edge
{
    int to,cost;
};
typedef pair<int,int> P; //first 是最短距离，second 是顶点的编号
int V;//顶点个数
vector<edge> G[MAXV];
int d[MAXV];
/*
需要优化的是数值的插入(更新)和取出最小值两个操作，因此使用堆就可以了。
把每个顶点当前的最短距离用堆来维护，在更新最短距离时，把对应的元素往根的方向移动
以满足堆的性质。
而每次从堆中取出的最小值就是下一次要用的顶点。这样堆中的元素共有 O(V)个，更新和取
出的操作有 O(E)次，因此整个算法的复杂度是 O(ElogV)。
下面是使用 STL 的 priority_queue 实现。在每次更新时往堆里插入当前最短距离和顶点的
值对。
插入的次数是 O(E)次，当取出的最小值不是最短距离的话，就丢弃这个值。这样整个算法也
可以在同样的时间内完成。
*/
void dijkstra(int s)
{
    priority_queue<P,vector<P>,greater<P> > que;
    memset(d,INF,sizeof d);
    d[s] = ;
    que.push(P(,s)); //把起点推入队列
    while(!que.empty())
    {
        P p = que.top();
        que.pop();
        int v = p.second; //顶点的编号
        if (d[v] < p.first) continue;
        ; i < G[v].size(); i++)
        {
            edge e = G[v][i];
            if (d[e.to] > d[v] + e.cost)
            {
                d[e.to] = d[v] + e.cost;
                que.push(P(d[e.to],e.to));
            }
        }
    }
}