「题解」「CF850A」Five Dimensional Points

题目

点这里

题解

本题暴力可过，细节不必多说。

这里我主要是说明一下为什么当 \(n>11\) 时可以直接输出 \(0\) 。

首先，思考二维空间中，我们能保证最多能同时存在多少点，而还有好点存在？

答案是 \(5\) 个，为什么？

可以手画一下，二维平面内五个点构成“十”字结构。

在这种情况下，点数最多。

进行拓展——三维呢？提示：可以从二维进行拓展。

答案是 \(7\) 个，为什么？

首先，我们在三维坐标系中画出二维结论，大概是这个鸭子（注意，全都是直角）

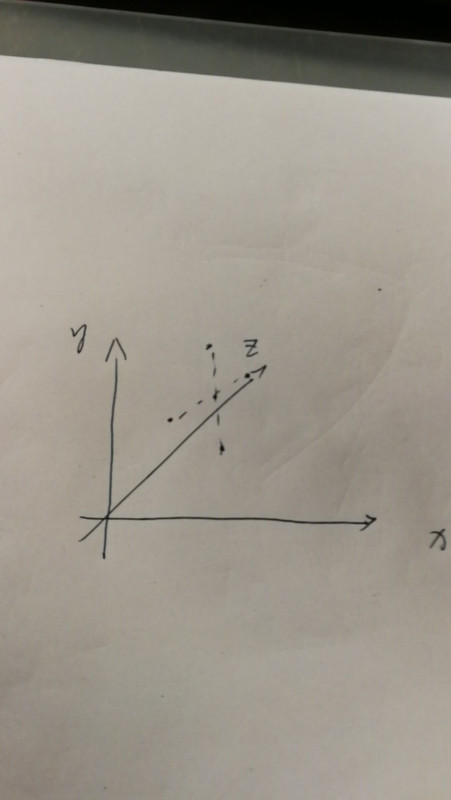
为了让点更多，我们从二维中学到了一个结构——“十”字结构，这个结构能让点最多。

推广一下——其实我们是在构造直角。

同时，还有一个结论——对于 \(A,B,C\) 三个点，如果 \(A\) 是好点，那么 \(B,C\) 一定是坏点。

为了让点数最多，我们贪心地让只让一个点成为好点，也就是只要其他的点不干扰这个点，点就可以随便加。

而加点时，只要我们遵循“十”字结构，那么点一定会是最多。

显然，在上图中，中间那个点是好点，那么我们只需要让它继续保持是好点，同时我们构造更多的直角，那么我们可以画出三维最多的图：

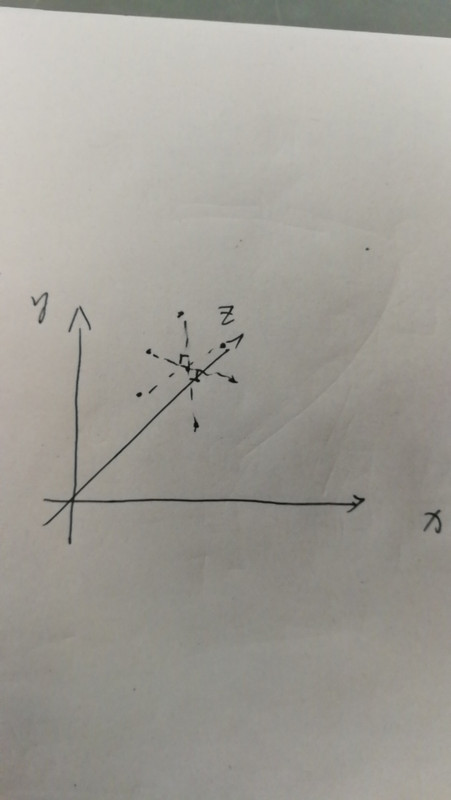
显然，这个时候有 \(7\) 个点，有点像两个“十”拼在一起，中间的轴是同一个。

至于更高维，我们画不出来了，但是可以推广。

多一维，相当于可以新增加一个“十”，那么加的点是多少？

很容易算，\(5-3=2\) ，为什么 \(-3\) ，因为我们为了保证还有一个好点，让多个“十”的中轴绑在一起，减掉轴上的 \(3\) 个点，自然而然增加了 \(2\) 个。

那么，四维最多 \(9\) 个，五维 \(11\) 个。

因而当 \(n>11\) 时，直接输出 \(0\) 即可。

代码

#include<cstdio>

#define rep(i,__l,__r) for(signed i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(signed i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define uint unsigned int
#define pii pair< int,int >
#define Endl putchar('\n')
// #define FILEOI
// #define int long long
// #define int unsigned

#ifdef FILEOI
# define MAXBUFFERSIZE 500000
    inline char fgetc(){
        static char buf[MAXBUFFERSIZE+5],*p1=buf,*p2=buf;
        return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXBUFFERSIZE,stdin),p1==p2)?EOF:*p1++;
    }
# undef MAXBUFFERSIZE
# define cg (c=fgetc())
#else
# define cg (c=getchar())
#endif
template<class T>inline void qread(T& x){
    char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    if(f)x=-x;
}
inline int qread(){
    int x=0;char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    return f?-x:x;
}
// template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
    inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
    if(x<0)return (void)(putchar('-'),fwrit(-x));
    if(x>9)fwrit(x/10);
    putchar(x%10^48);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
    return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}

const int MAXN=1e3;

struct point{
    int a[6];
}p[MAXN+5];

int n,tail;
int ans[MAXN+5];
bool flg;int calc;

signed main(){
#ifdef FILEOI
    freopen("file.in","r",stdin);
    freopen("file.out","w",stdout);
#endif
    scanf("%d",&n);
    rep(i,1,n)rep(j,1,5)p[i].a[j]=qread();
    if(n>11)return puts("0"),0;
    rep(i,1,n){
        flg=false;
        rep(j,1,n)if(i^j){
            rep(k,1,n)if(k^i && k^j){
                calc=0;
                rep(t,1,5)calc+=(p[i].a[t]-p[j].a[t])*(p[i].a[t]-p[k].a[t]);
                if(calc>0){flg=true;break;}
            }
            if(flg)break;
        }
        if(!flg)ans[++tail]=i;
    }
    writc(tail,'\n');
    rep(i,1,tail)writc(ans[i],' ');
    Endl;
    return 0;
}