<软件工程基础>个人项目——数独

参见GitHub：https://github.com/1773262526/Software-Foundation

Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
计划	30	30
估计这个任务需要多少时间
开发	120	60
需求分析（包括学习新技术）	150	180
生成设计文档	120	120
设计复审（和同事审核设计文档）	60	60
代码规范	60	30
具体设计	90	90
具体编码	1440	1200
代码复审	120	180
测试	300	600
报告	120	180
测试报告	90	120
计算工作量	30	30
事后总结，并提出过程改进计划	45	30
合计	2775	2910

解题思路：

主要任务分为两部分，一个是生成数独，另一个是求解数独。

在生成数独方面，主要有两种方法

1. 通过求解数独，利用回溯等方法，不断对一个初始残缺数独局进行求解，得到满足数量的终局。
2. 通过对一个已知合法数独终局进行一定的变换，变换结果仍然满足数独规则，获得更多的数独终局

在第一种方法中，能够保证结果的互异性，但需要大量的计算，不断填充验证结果是否合法，极其浪费时间，所以我选择通过对已知数组的变换获得结果。

设计实现过程：

　　数独的生成和求解是一个相当广泛的既成题目，已经有很多前人总结了足够的方法，代码中主要的部分可以通过对网上既成的代码进行适当改进，所以没有必要闭门造轮。

　　经过查阅相关资料，比较简单容易实现的变换原则有：对两个数进行互换、两行/两列之间互换（只能在共同区域内互换，如第一列第四列不能互换）、整个三行/三列为一个块进行互换、九宫格的2.4.6.8宫进行轮转，这些操作都不会破坏原数独方阵的合法性。

3.27note:可以选择手动制作50个（时间充足的情况下可以使用更多）原始数独方阵，每次生成时随机选择其中一个作为模板，然后利用随机数随机多次进行上述操作，基本可以保证不出现重复方阵。

　　生成数独：

　　经过实践，3.27的想法能够成功实现大量不重复的方阵，但是由于随机数的不可控性、仍然不能100%保证生成方阵数量极大时的互异性，若采用生成之后进行验证的方法，既浪费空间，优惠耗费大量时间，所以尽量保证数独方阵的生成中必然不会出现重复个体。（下文随机生成数组的代码已经改换成全排列进行）。 　　

　　经过查阅，数独方阵的的每行可以由第一行经过推移特定位数得到，这种方法的到的方阵同样满足数独的规则。比如第2-9行分别将第一行右移3、6、1、4、7、2、5、8行。

　　使用这种方法，能够从数独生成阶段杜绝重复数独发生的可能性。由于固定了第一行首位数的选择，所以这种方法可以生成8！=40320种终局，在与前沿的转换规则相结合，则能够轻易满足1e6种数独终局的要求。例如，要求1e6种终局，则由1e6/40320=24，需要至少25种变换方法，所以我们需要令每25个方阵使用相同的第一行。由于我的数组方阵使用了字符串进行处理，所以进行行变换更加方便，我采用“第4-6行中任意两行互换” * “第7-9行中任意两行进行互换” * “第2/3行进行互换”，这样有32种变换方法，足够满足需求。

　　对生成的数组进行计数，每32个动用一个首行的排列方式。在相同的首行生成的32个数组中，奇数组前三行不变，偶数组的第二三行进行互换。在此基础上，通过4-6,7-9行的变换，能够组合出4 * 4种方式。

　　　　代码说明

//行互换操作

void exch_row(char sudu[][], int op)
{
    if (op % )
        switchsudo(sudu, , );
    op /= ;
    switch (op)
    {
    case :return;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    case :switchsudo(sudu, , ); switchsudo(sudu, , ); break;
    }
}

　　　　求解数独

　　最初为了能够尽快的找出数独的答案，采用了摒弃求解和搜索并行的方式，但是在实践中容易产生bug，且在实践中发现比经典回溯方法节约的时间完全无法察觉，另外在求解数独部分因为没有性能要求，所以可以认为用户没有在短时间内求解大量数独的需求，而对于少数数独的求解，不同算法之间的时间差几乎无法察觉，所以没必要为了节约极少的时间浪费较多精力。这里采用了经典的回溯法，每次遇到空的位置时查询1-9是否合法，若合法则进行下一层探索，直到行不通回退回来，继续回溯，目前没有遇到无法求解的数独，且所有测试数独都能瞬间给出答案。此处不再赘述。

void backtrace(char sudu[][], int cont)
{
    if (cont ==  || flag)
    {
        flag = ;
        return;
    }
    int row = cont / ;
    int col = cont % ;
    if (sudu[row][col] == '')
    {
        for (int i = ; i <= ; ++i)
        {
            sudu[row][col] = i + '';//赋值
            if (isPlace(sudu, cont)) //可以放
            {
                backtrace(sudu, cont + );//进入下一层
                if (flag)
                    return;
            }
        }
        sudu[row][col] = '';//回溯
    }
    else
        backtrace(sudu, cont + );
}

　　　　函数概述

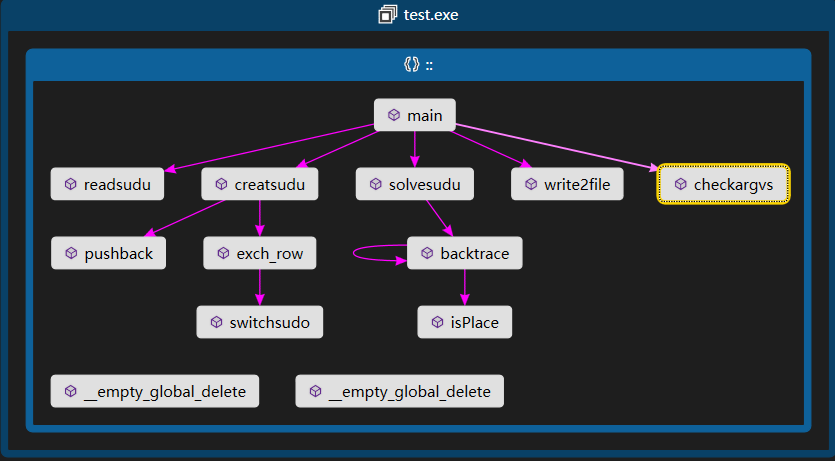
　　除主函数外有10个函数，调用关系如下：

　　程序流程图通过vs自动生成，见体系结构。只是画出了各个函数的调用联系，并没有注明跳转的判断条件。好像不如ida生成的舒服。。

性能分析、改进：使用生成1e6个数独终局进行性能测试。

　　首先是CPU占用率

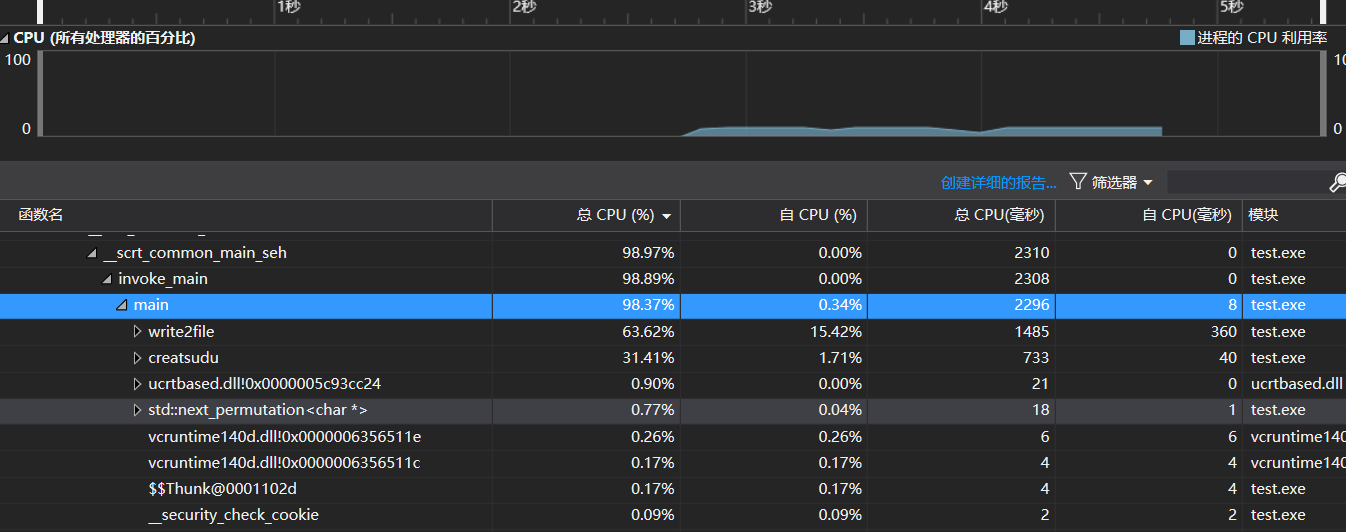
　然后是CPU采样、检测、内存分配和占用的检测

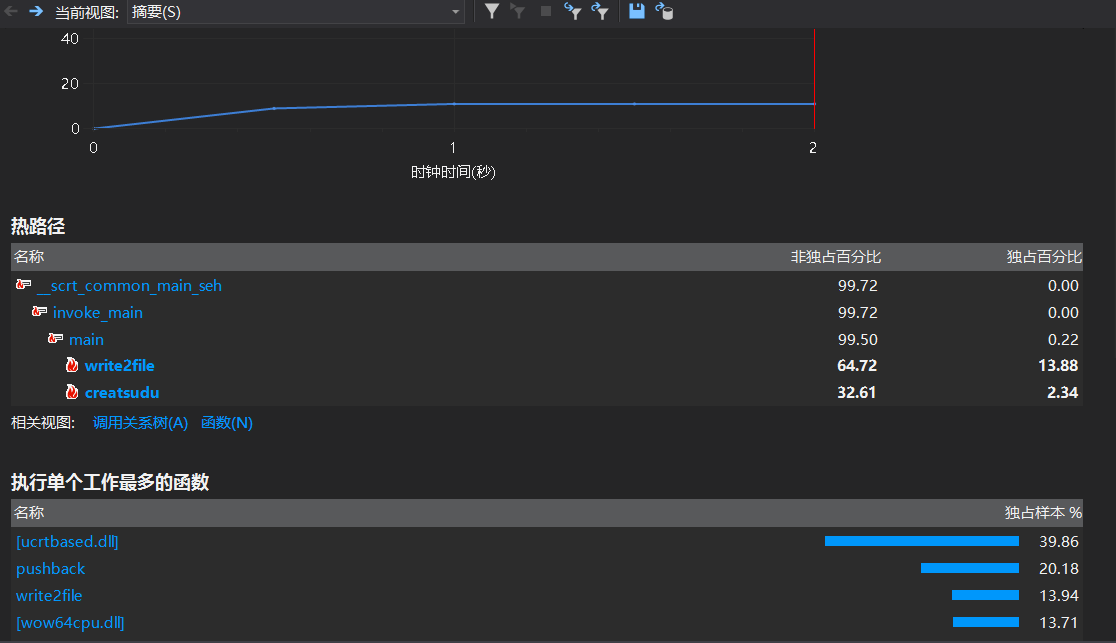
根据以上两项，不难发现瓶颈主要在于写入文件和生成数独中对第一行的后移。

　　首行的后移是解决方案的硬性要求，而且已经压缩到线性，无法再继续优化。

　　写入文件部分：输出是采用按字符输出，即从9*10的字符数组中一位一位的输出，在每个字符之间穿插空格换行。按照函数调用约定，会将参数传进寄存器，再将函数调用地址和返回地址分别压栈，在出栈时进行函数调用。这样每个数独方阵输出时需要多进行近两百次栈操作，数组数量极大时会在函数调用方面浪费很多时间，所以直接改成在程序中将方阵字符和空格等直接编入一个字符串，只执行一次写文件函数，将整个字符串写入，理论上能够节省一定的时间。

//改进后的写入操作

//后移操作

void pushback(char su[], int m, char sou[])
{
    char cop[] = {  };
    strcpy(cop, sou);
    int i;
    for (i = ; i < ; i++)
        su[(i + m) % ] = cop[i];
}

　　　　经过改进，能够在1-2秒内生成1e6组数组并写入文件（比之前并没有可见的提高），足以满足性能需求，

　　　　求解数独部分因为没有性能要求，便不再展示其性能分析部分。

单元测试部分

　　经过断断续续三四天的纠缠，总算弄好了单元测试部分。可以使用vs提供的单元测试项目进行单元测试，使用Assert断言某项。　　　　　　　　　　///困死了，，再不睡要去见图灵了

　　单元测试部分还是比较麻烦，因为在实现代码的时候，已经经过重复的输出测试和相关debug环节，基本排除掉了bug，能够在各种情况下实现预期的输出，而且进行测试的用例是学生自己提供，能够想到的坑早已经和同学交流过，并且在编码中解决。所以这项工作其实非常鸡肋，唯一的作用就是学习一下单元测试的使用，算是提前学习了这种操作。

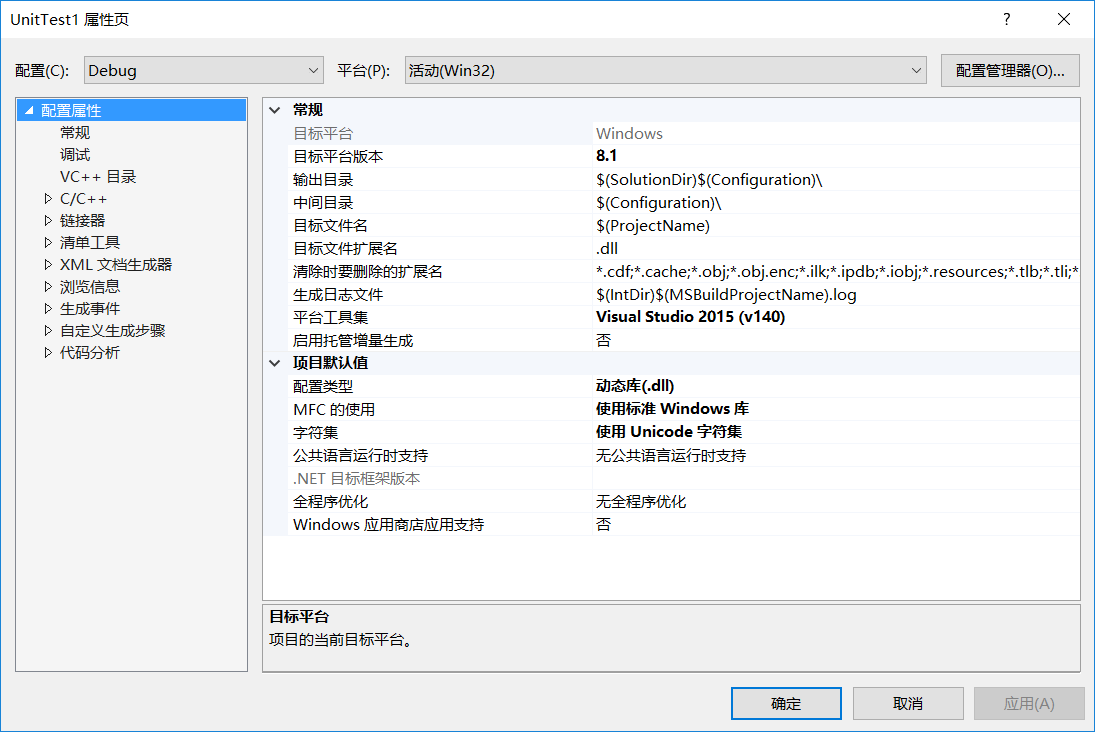
　　之前没有用过单元测试，还是靠着百度和同学的帮助下，才成功找到了新建单元测试项目的按钮，但还是遇到能够成功编译单元测试代码，但是在测试资源管理器不能显示测试结果。之后发现是项目的配置在之前胡改成了debug（活动）还有链接库也根据其他的博客改的面目全非，改回debug、动态链接库就能够正常显示。

     

　　在测试模块中，通过自行定义变量，可以调用数独项目中的函数，根据断言返回值或者变量的改变，判断函数是否能够在不同情况下，实现预期的功能。

　　代码覆盖率分析

　　　　代码覆盖率在“测试/窗口/代码覆盖率结果”或选择“分析代码覆盖率”。

　　

　　　　在最初的代码覆盖率分析的时候，发生了一些意外，由于未知原因导致明明运行的测试，却提示未检测二进制文件。

　　　　　　经过几番尝试在本项目中始终无法正确得出结果，转移到同学的vs2017上经过配置项目属性，能够得到，判断应该是在之前尝试乱改属性进行单元测试的时候改崩了。

　　　　　　另新建了项目，确定活动解决方案平台为x86，两个项目文件的配置都是debug，平台选择win32便能够顺利得出覆盖率分析。

　　　　　　

　　　　　　

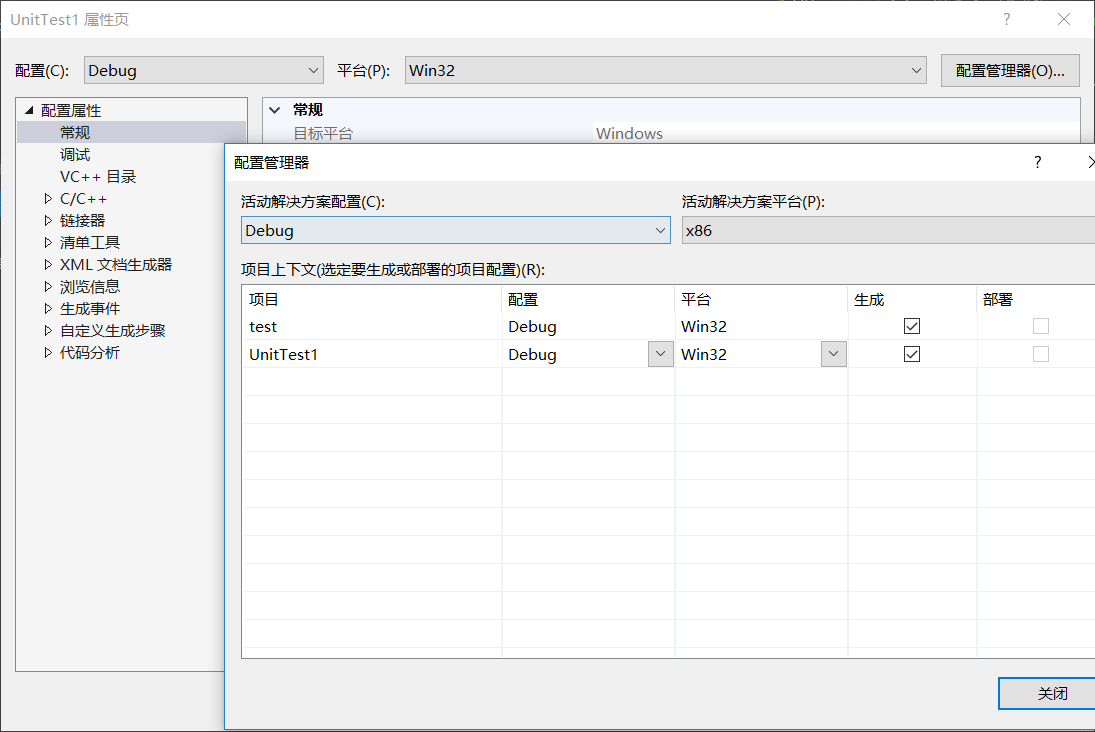
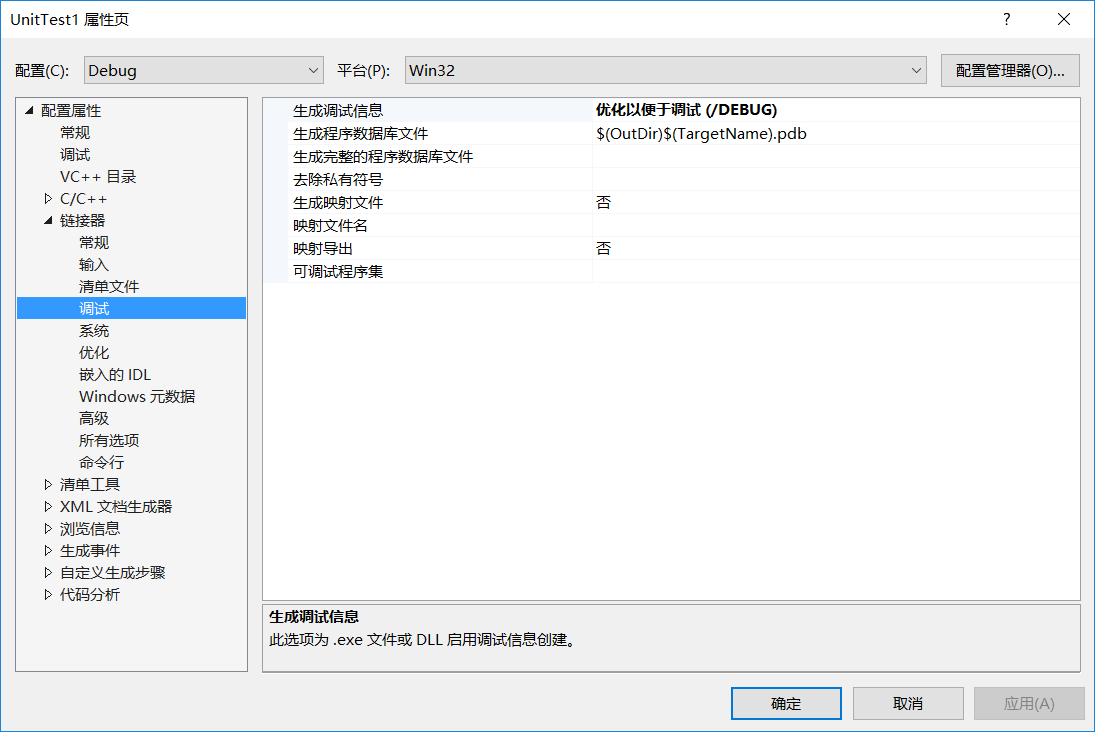
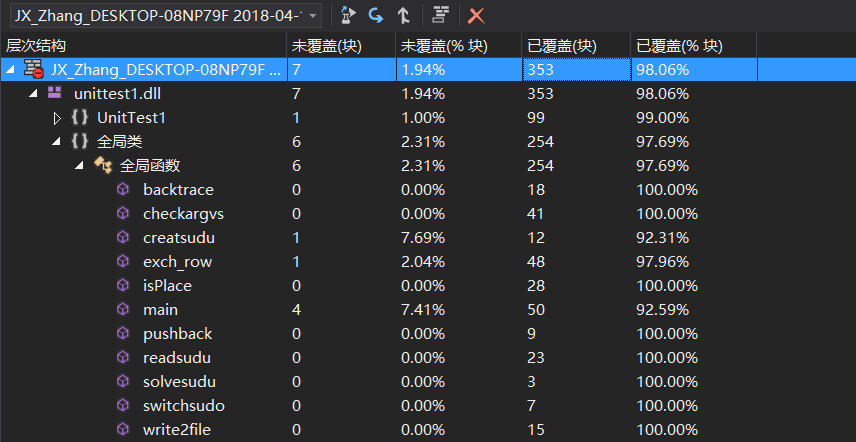
　　　　　　最后晒一下几经修改把代码覆盖率从80.74提高到98.06。

　　　　　　

　　　　　　最终整体覆盖率和各函数的测试覆盖率。

　　　　　　

我想说

　　随着博客的完工，GitHub的同步也逐步完成，旷日持久的单人项目终于宣告结束。这段时间，除了喜闻乐见的bug，更让人闹心的应该算是单元测试和覆盖率这些魔性的新东西了。之前完全没有用过这玩意，老师也完全没有指导，网上又没有可靠的教程，甚至是错误的引导（雾），单元测试部分按照错误的引导乱改配置，直接导致了覆盖率测试的严重问题。

　　不过也算是一次历练吧，从之前的码题，到真正自己去按照流程去做这么一个东西，确实多了很多意料之外的困难，为了能够解决这些问题，也经历了连续一周熬到一点的舒爽，同时也学到了很多东西，不过也真的耽误了很多其他的学习。