基于在树上走的DP问题

笔者已经很久没有打过题解了，如果打题解，就总是要连着一个知识点来打题解。

最近做过一共两道这样的题目。笔者认为这样的题有较强的可拓展性，比较有意义。

所以就打一篇博客。

---

问题概述

先说说这是个什么样的问题。

给你一棵树（无向），从某个点开始走，每到一个节点可以得到一些分数，如果这个点之前已经被走过，那就不能得到这些分数。每走一个边（或点）都会有一些代价。问在一定的代价内，最多的分数。

可能光是看文字不好理解题目大意，这里放道例题。

例题 JZOJ5819 大逃杀

Description

自从 Y 君退役之后，她就迷上了吃鸡，于是她决定出一道吃鸡的题。

Y 君将地图上的所有地点标号为 1 到 n，地图中有 n − 1 条双向道路连接这些点，通过一条 双向道路需要一定时间，保证从任意一个点可以通过道路到达地图上的所有点。

有些点上可能有资源，Y 君到达一个有资源的点后，可以选择获取资源来使自己的武力值增 加 wi，也可以选择不获取资源。如果 Y 君获取了一个点上的资源，这个点上的资源就会消失，获 取资源不需要时间。

有些点上可能有敌人，Y 君到达一个有敌人的点后，必须花费 ti 秒伏地与敌人周旋，并最终 将敌人消灭。如果 Y 君消灭了一个点上的敌人，这个点上的敌人就会消失。Y 君不能无视敌人继 续前进，因为这样会被敌人攻击。

如果一个点上既有资源又有敌人，Y 君必须先消灭敌人之后才能获取资源，否则就会被敌人 突袭。

游戏开始时，Y 君可以空降到任意一个点上，接下来，她有 T 秒进行行动，T 秒后她就必须 前往中心区域送快递。Y 君希望她前往中心区域送快递时，武力值尽可能大，请你帮助 Y 君设计 路线，以满足她的要求。你只需输出 T 秒后 Y 君的武力值。

Input

第一行由单个空格隔开的两个正整数 n, T，代表点数和时间。

第二行 n 个由单个空格隔开的非负整数代表 wi，如果 wi = 0 代表该点没有武器，

第三行 n 个由单个空格隔开的非负整数代表 ti，如果 ti = 0 代表该点没有敌人。

接下来 n − 1 行每行由单个空格隔开的 3 个非负整数 a, b, c 代表连接 a 和 b 的双向道路，通 过这条道路需要 c 秒。

Output

输出一行一个整数代表 T 秒后 Y 君的武力值。

Sample Input

17 54

5 5 1 1 1 25 1 10 15 3 6 6 66 4 4 4 4

0 1 3 0 0 0 1 3 2 0 6 7 54 0 0 0 0

1 8 3

2 8 3

8 7 7

7 13 0

7 14 0

15 14 2

16 14 3

17 14 5

7 9 4

9 10 25

10 11 0

10 12 0

7 6 20

3 6 3

3 4 3

3 5 3

Sample Output

68

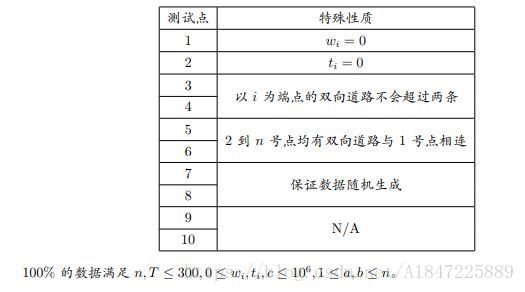
Data Constraint

题目的大意就是在一棵树上，从一个点出发。每走一条边需要花一定时间。每到一个点，如果之前这个点没有走过，就要花一定时间，而且获得一定分数。问在T" role="presentation">TT单位时间内，最多可以得到多少分数（初始点有你自己确定）。

---

先思考思考~

具体的解法

这题看上去就是一道树形DP对吧，一副暴力不好打的样子。

首先，让我们假设一下初始点是固定的。

有个显然的结论：一个子树不可能重复进入两遍。

如果它重复进入了两遍，不如一次性走完，反正每个点的分数只能得到一次。

树形DP咋打？

设fi,j" role="presentation">fi,jfi,j表示在以i" role="presentation">ii为根的子树中，花了j" role="presentation">jj的时间，最终回到i" role="presentation">ii的最大分数。

设gi,j" role="presentation">gi,jgi,j表示在以i" role="presentation">ii为根的子树中，花了j" role="presentation">jj的时间，最终不一定回到i" role="presentation">ii的最大分数。

为什么这么设？树形DP嘛，将总的问题分解成每个子树中的问题，然后一一解决。

对于这题来说，一个子树对答案做出的贡献也就两种，要么走一圈之后出去再走其它的子树，要么走一圈之后永远待在子树中别出来了。

很明显，fi,j≤gi,j" role="presentation">fi,j≤gi,jfi,j≤gi,j

初值fi,ti=gi,ti=wi(fi,others=−∞)" role="presentation">fi,ti=gi,ti=wi(fi,others=−∞)fi,ti=gi,ti=wi(fi,others=−∞)，不要问我为什么，太显然了……

在树形DP时，枚举子树，设这个子树的根节点为son" role="presentation">sonson。

先考虑f" role="presentation">ff的转移。

显然情况只有一种：

从i" role="presentation">ii出发，走son" role="presentation">sonson之前的子树，回到i" role="presentation">ii，然后又去son" role="presentation">sonson子树中转一圈，最终转回到i" role="presentation">ii。

fi,j⇐fi,j−2∗len−k+fson,k" role="presentation">fi,j⇐fi,j−2∗len−k+fson,kfi,j⇐fi,j−2∗len−k+fson,k

再考虑g" role="presentation">gg的转移。

这个情况有两种，分别是：

1. 从i" role="presentation">ii出发，走son" role="presentation">sonson之前的子树，回到i" role="presentation">ii，然后又去son" role="presentation">sonson子树中，永远地留在son" role="presentation">sonson子树里。

gi,j⇐fi,j−len−k+gson,k" role="presentation">gi,j⇐fi,j−len−k+gson,kgi,j⇐fi,j−len−k+gson,k

2. 另一个情况相对难理解。从i" role="presentation">ii出发，走son" role="presentation">sonson和son" role="presentation">sonson之前的子树，其中在son" role="presentation">sonson子树中转了一圈后回来。最终，在i" role="presentation">ii点或son" role="presentation">sonson之前的子树中停下来。也就是说，son" role="presentation">sonson子树只是作为一个中转站，转过一圈之后走出来，然后到别处停下来。

gi,j⇐gi,j−len∗2−k+fson,k" role="presentation">gi,j⇐gi,j−len∗2−k+fson,kgi,j⇐gi,j−len∗2−k+fson,k

知道了f" role="presentation">ff和g" role="presentation">gg，那就可以算出从根开始的最优解，即maxgroot,j" role="presentation">maxgroot,jmaxgroot,j。

所以我们可以枚举根，然后对于每个根做一遍树形DP。

时间复杂度O(n2T2)" role="presentation">O(n2T2)O(n2T2)，显然过不了。

咋办？

我们之前求的是从根出发，那么不妨思考一下，在这个子树中，不一定会从根节点出发的情况。

设hi,j" role="presentation">hi,jhi,j表示在以i" role="presentation">ii为根的子树中，花了j" role="presentation">jj的时间，从i" role="presentation">ii子树中的某个点出发，经过i" role="presentation">ii点，最终在i" role="presentation">ii子树中停下来。

显然初值hi,ti=wi" role="presentation">hi,ti=wihi,ti=wi（其实初值这种东西真心不想打进博客里，只是可能有些童鞋需要……）

思考一下，情况有三种（比起前面的相对难理解，注意仔细思考）：

1. 将i" role="presentation">ii以及son" role="presentation">sonson之前的子树求出的g" role="presentation">gg值，son" role="presentation">sonson里面的子树求出的g" role="presentation">gg值，合并在一起。

怎么理解呢？形象地理解一下，f" role="presentation">ff、g" role="presentation">gg、h" role="presentation">hh值就像是条绳子所作出的贡献。其中f" role="presentation">ff至少两端在根节点上，g" role="presentation">gg至少一端在根节点上，h" role="presentation">hh的端点可以不再根节点上。而这样合并就是将两条g" role="presentation">gg绳各自的一头接在了一起，形成一个新的h" role="presentation">hh绳。

hi,j⇐gi,j−len−k+gson,k" role="presentation">hi,j⇐gi,j−len−k+gson,khi,j⇐gi,j−len−k+gson,k

2. 将i" role="presentation">ii的h" role="presentation">hh绳中，插入新的一段son" role="presentation">sonson的f" role="presentation">ff绳。这样就可以保证插入之后绳子没有中断。

hi,j⇐hi,j−2∗len−k+fson,k" role="presentation">hi,j⇐hi,j−2∗len−k+fson,khi,j⇐hi,j−2∗len−k+fson,k

3. 和上面类似，在son" role="presentation">sonson的h" role="presentation">hh绳中，插入新的一段i" role="presentation">ii以及son" role="presentation">sonson之前子树的f" role="presentation">ff绳。

hi,j⇐fi,j−2∗len−k+hson,k" role="presentation">hi,j⇐fi,j−2∗len−k+hson,khi,j⇐fi,j−2∗len−k+hson,k

这样求出所有的h" role="presentation">hh值，这样，答案即maxhi,j" role="presentation">maxhi,jmaxhi,j

对了，需要格外注意一下转移的顺序，按照h" role="presentation">hh、g" role="presentation">gg、f" role="presentation">ff的顺序（不然可能会出现叠加），还有一个六年级的同学都应该知道的j" role="presentation">jj要倒着枚举。

时间复杂度O(nT2)" role="presentation">O(nT2)O(nT2)，可以过。

代码（模板？）

using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 300
#define MAXTIME 300
inline void MAX(long long &a,long long b) {a<b?a=b:0;}//尝试更新
int n,time;
int w[MAXN+1],t[MAXN+1];
struct EDGE
{
    int to,len;
    EDGE *las;
} e[MAXN*2+1];
int ne;
EDGE *last[MAXN+1];
void link(int u,int v,int len){e[++ne]={v,len,last[u]};last[u]=e+ne;}
bool vis[MAXN+1];
long long f[MAXN+1][MAXTIME+1],g[MAXN+1][MAXTIME+1],h[MAXN+1][MAXTIME+1];
void dfs(int);
long long ans;
int main()
{
    freopen("toyuq.in","r",stdin);
    freopen("toyuq.out","w",stdout);
    scanf("%d%d",&n,&time);
    for (int i=1;i<=n;++i)
        scanf("%d",&w[i]);
    for (int i=1;i<=n;++i)
        scanf("%d",&t[i]);
    for (int i=1;i<n;++i)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        link(a,b,c),link(b,a,c);
    }
    dfs(1);
    for (int i=1;i<=n;++i)
        for (int j=t[i];j<=time;++j)
            ans=max(ans,h[i][j]);
    printf("%lld\n",ans);
    return 0;
}
void dfs(int x)
{
    vis[x]=1;
    memset(f[x],254,sizeof f[x]);
    memset(g[x],254,sizeof g[x]);
    memset(h[x],254,sizeof h[x]);
    if (t[x]>time)//这是一个剪枝，很显然，如果来x点所花费的时间大于time，那么就不用玩了
    {
        for (EDGE *ei=last[x];ei;ei=ei->las)
            if (!vis[ei->to])
                dfs(ei->to);
    }
    else
    {
        f[x][t[x]]=g[x][t[x]]=h[x][t[x]]=w[x];
        for (EDGE *ei=last[x];ei;ei=ei->las)
            if (!vis[ei->to])
            {
                dfs(ei->to);
                for (int i=time;i>=t[x];--i)
                {
                    //循环方式有些奇怪，其实就是将两种转移分开，少打一些if语句
                    int j=t[ei->to];
                    for (;i-ei->len-j-ei->len>=t[x];++j)
                    {
                        //下面可能会打得有些丑陋吧。
                        //为了方便理解，我将2*ei->len拆开成两个，分别表示进出.
                        //这个顺序是必须要注意，不然可能会出现叠加的情况。当然，如果你多开一个维，或者是打滚动，我也懒得理你。
                        //把一个状态的转移全部分开来打？显然不行啊，不然也可能会出现叠加。只能分开一些转移没有可能是来自当前的状态的式子。
                        MAX(h[x][i],max(g[x][i-ei->len-j]+g[ei->to][j],max(h[x][i-ei->len-j-ei->len]+f[ei->to][j],f[x][i-ei->len-j-ei->len]+h[ei->to][j])));
                        MAX(g[x][i],max(f[x][i-ei->len-j]+g[ei->to][j],g[x][i-ei->len-j-ei->len]+f[ei->to][j]));
                        MAX(f[x][i],f[x][i-ei->len-j-ei->len]+f[ei->to][j]);
                    }
                    for (;i-ei->len-j>=t[x];++j)
                    {
                        MAX(h[x][i],g[x][i-ei->len-j]+g[ei->to][j]);
                        MAX(g[x][i],f[x][i-ei->len-j]+g[ei->to][j]);
                    }
                }
            }
    }
}

总结

可能会有些难以理解把，不过好好地思考思考还是可以理解的。这个树形DP比较奇妙。

以后见到这种在树上走的DP问题，就可以用类似这样的方法，或者是扩展。

莫名其妙的，我觉得这个DP方法很有意义。