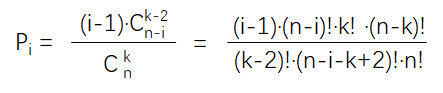UPC 2019年第二阶段我要变强个人训练赛第十六场

传送门：

　　[1]:UPC比赛场

　　[2]:UPC补题场

F.gu集合（数论）

•题目描述

 题目描述：
 Dew有一个长为n的集合S。
 有一天，他想选k个不同的元素出来做游戏。
 但是Dew只有两只手，所以他只能先选出k个元素，然后拿出这k个元素中最小的两个。
 事实上，Dew更喜欢这k个元素中第二小的那个。
 因此他会记一个集合T的第二小值为g(T)。
 此时Dew可以获得c^g(T)!的得分，其中c是一个常数，!表示阶乘。
 现在你需要求出Dew从集合S中选出k个元素后，他的期望得分对998244353取模的结果。

 输入：
 输入共两行。
 第一行三个正整数n,k,c，分别表示集合S的大小，Dew要选的元素个数，和常数c。
 第二行n个互不相同的正整数ai，表示集合S中的元素。保证集合s升序。

 输出：
 输出一行一个非负整数，表示Dew的期望得分对998244353取模的结果。

题目描述、输入、输出

 样例输入

 样例输出
 

样例输入输出

样例解释

•题解

　　在tyk的帮助下顺利AC；

　　下面开始扯淡；

　　第 i 个数 ai 可以作为第二小的数的条件是：

　　　　①存在比 a_i 小的数，即 i > 1；

　　　　②比 a_i 大的数的个数要多于 k-2，即 n-i ≥ k-2；

　　对于满足条件的 ai，共有

　　，

　　那么得到 ai 的概率为：

　　

　　最终答案就是 ∑ P_i×c^a_i!；

•细节处理

　　对于除法取模Pi%MOD直接用逆元处理即可，关键是 c^a_i! 该如何处理？

　　根据费马小定理：a^p-1 ≡ 1 (mod p) 可知循环节为 p-1（a^p-1 ≡ a⁰ (mod p) ⇔ 0~p-2 为一个循环） ；

　　即 a^x ≡ a^x%(p-1) (mod p) ；

　　那么 c^a_i! ≡ c^a_i!%(p-1)(mod p)；

　　而 a_i!%(p-1) 可以提前预处理出来；

•Code

 #include<bits/stdc++.h>
 using namespace std;
 #define ll long long
 const int MOD=;
 const int maxn=5e5+;

 int n,k,c;
 int a[maxn];
 ll fact[maxn];///fact只开到5e5就足够了，如果开到1e7，返回内存超限
 ll g[(int)1e7+];

 ll qPow(ll a,ll b)
 {
     ll ans=;
     a %= MOD;
     while(b)
     {
         if(b&)
             ans=ans*a%MOD;

         a=a*a%MOD;
         b >>= ;
     }
     return ans;
 }
 int Solve()
 {
     fact[]=g[]=;
     for(int i=;i < maxn;++i)
         fact[i]=i*fact[i-]%MOD;
     for(int i=;i <= (int)1e7;++i)
         g[i]=i*g[i-]%(MOD-);

     ll ans=;
     for(int i=;i <= n;++i)
     {
         if(n-i < k-)
             break;

         ll b=fact[k-]*fact[n-i-k+]%MOD*fact[n]%MOD;///概率的分母取模后的结果
         ///qPow(b,MOD-2)为逆元
         ll p=(i-)*fact[n-i]%MOD*fact[k]%MOD*fact[n-k]%MOD*qPow(b,MOD-)%MOD;

         ans += p*qPow(c,g[a[i]]);
         ans %= MOD;
     }
     return ans;
 }
 int main()
 {
     scanf("%d%d%d",&n,&k,&c);
     for(int i=;i <= n;++i)
         scanf("%d",a+i);

     printf("%d\n",Solve());

     return ;
 }

•感悟

　　满满的数论知识，有些知识点早就学过，但就学死了，没能做到活用；

　　看来，还是得多做题，多总结，要活学活用；

---

H.奇迹（暴力+欧拉筛法）

•题目描述

题目描述
相信奇迹的人，本身就和奇迹一样了不起。——笛亚 《星游记》
我们称一个日期为一个八位数，第1~4位构成年，第5~6位构成月，第7~8位构成日，不足位数用0补足。
同时，要求日期所代表的这一天真实存在，且年的范围为1~。
出现奇迹的日期都存在相同的特点：由“日”组成的两位数，由“月+日”组成的四位数，由“年+月+日”组成的八位数均为质数。
但并不是所有存在这样特点的日期都一定会出现奇迹。
现在，你得到了一个可能会出现奇迹的日期，然而不幸的是这个日期却是残缺的，八位中可能有若干位无法确定。
你需要知道这个日期有多少种可能，这样你才能做好充足的准备去迎接奇迹的到来。

输入
本题有多组数据。
第一行一个正整数T，表示数据组数。
接下来的T行，每行一个八位字符串。
其中第i位如果为 '-'，则表示日期的第i位无法确定，否则表示日期的第i位为字符串中第i位上的数字。

输出
对每组数据，一行一个整数，表示答案。

题目描述、输入、输出

样例输入

---

样例输出

样例输入输出

--- 的  种可能的日期如下：

一共10个测试点，记c为八位字符串中 '-' 的个数。
对前9个测试点，在第i个测试点中保证c=i-。
对100%的数据保证1≤T≤。

提示

•题解（暴力+欧拉筛法预处理）

　　枚举所有可能的日期，并判断①其是否符合字符串 s；②符合正常日期；

　　在满足上述条件的请款下，并判断其是否符合出现奇迹的要求，如果符合，ans++；

•Code

 #include<bits/stdc++.h>
 using namespace std;
 #define mem(a,b) memset(a,b,sizeof(a))
 const int day[][]={{,,,,,,,,,,,,},
                       {,,,,,,,,,,,,}/**闰年*/};
 char s[];

 int prime[];
 bool isPrime[];
 void Prime()
 {
     mem(isPrime,true);
     int cnt=;
     isPrime[]=false;
     for(int i=;i < ;++i)
     {
         if(isPrime[i])
             prime[++cnt]=i;
         for(int j=;j <= cnt && prime[j]*i < ;++j)
         {
             isPrime[i*prime[j]]=false;
             if(i%prime[j] == )
                 break;
         }
     }
 }
 bool isRun(int y)
 {
     return (y% !=  && y% == )||(y% == );
 }
 bool isSatY(int y)
 {
     if(s[] != '-' && (s[]-'') != y/)
         return false;
     if(s[] != '-' && (s[]-'') != y/%)
         return false;
     if(s[] != '-' && (s[]-'') != y/%)
         return false;
     if(s[] != '-' && (s[]-'') != y%)
         return false;

     return true;
 }
 bool isSatM(int m)
 {
     if(s[] != '-' && (s[]-'') != m/)
         return false;
     if(s[] != '-' && (s[]-'') != m%)
         return false;

     return true;
 }
 bool isSatD(int d)
 {
     if(s[] != '-' && (s[]-'') != d/)
         return false;
     if(s[] != '-' && (s[]-'') != d%)
         return false;

     return true;
 }
 int Solve()
 {
     int ans=;
     for(int y=;y <= ;y++)
     {
         if(!isSatY(y))///判断y是否符合s
             continue;

         for(int m=;m <= ;m++)
         {
             if(!isSatM(m))///判断m是否符合s
                 continue;

             for(int d=;d <= day[isRun(y)][m];d++)///判断m是否符合s
                 if(isSatD(d) && isPrime[m*+d] && isPrime[d] && isPrime[y*+m*+d])
                     ans++;
         }
     }
     return ans;
 }
 int main()
 {
     Prime();///预处理1~99991232内的所有素数

     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%s",s+);
         printf("%d\n",Solve());
     }
     return ;
 }

•思考

上述代码耗时：

如果将三重循环的顺序颠倒以下，改成如下顺序：

 int Solve()
 {
     int ans=;
     for(int d=;d <= ;++d)
     {
         if(!isPrime[d] || !isSatD(d))
             continue;
         for(int m=;m <= ;++m)
         {
             if(!isPrime[d+m*] || !isSatM(m))
                 continue;
             for(int y=;y <= ;++y)
             {
                 if(!isPrime[y*+m*+d] || d > day[isRun(y)][m] || !isSatY(y))
                     continue;
                 ans++;
             }
         }
     }
     return ans;
 }

耗时：

快了将近三百毫秒！！！

对于此题而言，颠倒一下顺序，枚举的情况会少一下；

•坑

起初，我用vector<>存储的prime，返回 TLE，改成 int 后，AC；

看来，动态分配空间还是比提前计算出所需的空间慢一些；