UOJ#428. 【集训队作业2018】普通的计数题

#428. 【集训队作业2018】普通的计数题

模型转化好题

所以变成统计有标号合法的树的个数。

合法限制：

1.根标号比子树都大

2.如果儿子全是叶子，数量B中有

3.如果存在一个儿子不是叶子，数量A中有

然后考虑DP

直接枚举根的儿子的情况

cdq分治NTT还是很恶心的

不光是自己卷自己，还是互相卷

进行一番化简和平移之后，可以转化为cdq分治NTT的形式：

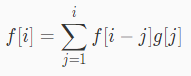
怎么好做怎么来。

反正我最后推的式子有如下特点（式子就不写了）：

为了方便，钦定g[0],f[0],g[1],f[1]都是0

对于f，a是固定的，a向右平移一下，然后就是cdq分治的模板题了

对于g，当cdq的分治区间l不是0的时候，要F作为[l,mid],G作为[ql,qr]，和G作为[l,mid],F作为[ql,qr]做两遍

这样其实剩下g[n]=g[0]*f[n]，但是g[0]=0，所以不用管

代码：

const int N=+;
int jie[N],inv[N];
int f[N],g[N];
int n,sa,sb;
int ta[N],b[N],a[N];
void divi(int l,int r,int ql,int qr){
    // cout<<" divi "<<l<<" "<<r<<" ql "<<ql<<" qr "<<qr<<endl;
    if(l==&&r==){
        f[]=f[]=g[]=g[]=;
        return;
    }
    if(l==r){
        f[l]=ad(mul(f[l],jie[l-]),b[l-]);
        g[l]=ad(f[l],mul(g[l],jie[l-]));
        f[l]=mul(f[l],inv[l-]);
        g[l]=mul(g[l],inv[l]);
        return;
    }
    int mid=(l+r)>>;
    int qmd=(ql+qr)>>;
    divi(l,mid,ql,qmd);
    Poly A,G;
    A.resize(qr-ql+);
    G.resize(mid-l+);
    for(reg i=ql;i<=qr;++i){
        A[i-ql]=a[i];
    }
    for(reg i=l;i<=mid;++i){
        G[i-l]=g[i];
    }
    A*=G;
    for(reg i=mid+;i<=r;++i){
        f[i]=ad(f[i],A[i-l]);
    } 

    if(l==){
        Poly F;G.clear();
        F.resize(mid-l+);
        G.resize(mid-l+);
        for(reg i=l;i<=mid;++i){
            F[i-l]=f[i];
            G[i-l]=g[i];
        }
        F=F*G;
        for(reg i=mid+;i<=r;++i){
            g[i]=ad(g[i],F[i]);
        }
    }else{
        Poly F;G.clear();
        F.resize(qr-ql+);
        G.resize(mid-l+);
        for(reg i=l;i<=mid;++i){
            G[i-l]=g[i];
        }
        for(reg i=ql;i<=qr;++i){
            F[i-ql]=f[i];
        }
        F=F*G;
        for(reg i=mid+;i<=r;++i){
            g[i]=ad(g[i],F[i-l]);
        }
        F.clear();G.clear();
        F.resize(mid-l+);
        G.resize(qr-ql+);
        for(reg i=ql;i<=qr;++i){
            G[i-ql]=g[i];
        }
        for(reg i=l;i<=mid;++i){
            F[i-l]=f[i];
        }
        F=F*G;
        for(reg i=mid+;i<=r;++i){
            g[i]=ad(g[i],F[i-l]);
        }
    }
    divi(mid+,r,ql,qmd);
}
int main(){
    rd(n);rd(sa);rd(sb);int x;
    for(reg i=;i<=sa;++i){rd(x);ta[x]=;}
    for(reg i=;i<=sb;++i){rd(x);b[x]=;}
    if(n==){
        puts("");return ;
    }
    int m;
    for(m=;m<=n;m<<=);
    jie[]=;
    for(reg i=;i<=m;++i) jie[i]=mul(jie[i-],i);
    inv[m]=qm(jie[m],mod-);
    for(reg i=m-;i>=;--i) inv[i]=mul(inv[i+],i+);

    for(reg i=;i<=m;++i){
        a[i]=mul(ta[i-],inv[i-]);
    }
    a[]=;

    divi(,m-,,m-);
    ll ans=f[n];
    ans=mul(ans,jie[n-]);
    ot(ans);
    return ;
}

树形结构很巧妙啊

f，g互相卷的分治NTT第一次写，还是举一个0,1,2,3,4,5,6,7的例子最好理解了！