自己动手实现java数据结构（二） 链表

1.链表介绍

　　前面我们已经介绍了向量，向量是基于数组进行数据存储的线性表。今天，要介绍的是线性表的另一种实现方式---链表。

　　链表和向量都是线性表，从使用者的角度上依然被视为一个线性的列表结构。但是，链表内部存储数据的方式却和向量大不相同：链表的核心是节点。节点存储"数据"的同时还维护着"关联节点的引用"。要理解链表，首先必须理解链表的内部节点结构。

　　最简单的链表结构是单向链表，单向链表中的内部节点存储着数据(data)和其关联的下一个节点的引用(next)。

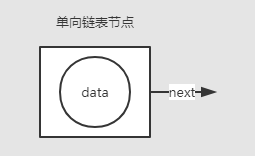　　　　data代表存储的数据，next代表所关联下一个节点的引用

　　一个逻辑上存储了【a，b，c】三个元素的链表，长度为3，三个元素分别被三个节点存储。

　　

2.链表ADT介绍

　　链表作为线性表的一种，和向量一样实现了List接口。

/**
 * 列表ADT 接口定义
 */
public interface List <E> {

    /**
     * @return 返回当前列表中元素的个数
     */
    int size();

    /**
     * 判断当前列表是否为空
     * @return 如果当前列表中元素个数为0，返回true；否则，返回false
     */
    boolean isEmpty();

    /**
     * 返回元素"e"在列表中的下标值
     * @param e     查询的元素"e"
     * @return      返回"obj"元素在列表中的下标值;
     *               "obj"不存在于列表中，返回-1;
     */
    int indexOf(E e);

    /**
     * 判断元素"e"是否存在于列表中
     * @param e     查询的元素"e"
     * @return      返回"true"代表存在，返回"false"代表不存在;
     */
    boolean contains(E e);

    /**
     * 在列表的末尾插入元素"e"
     * @param e 需要插入的元素
     * @return  插入成功，返回true；否则返回false
     * */
    boolean add(E e);

    /**
     * 在列表的下标为"index"位置处插入元素"e"
     * @param index 插入位置的下标
     * @param e     需要插入的元素
     */
    void add(int index, E e);

    /**
     *  从列表中找到并且移除"e"对象
     * @param e   需要被移除的元素"e"
     * @return      找到并且成功移除返回true；否则返回false
     */
    boolean remove(E e);

    /**
     * 移除列表中下标为"index"位置处的元素
     * @param index  需要被移除元素的下标
     * @return      返回被移除的元素
     */
    E remove(int index);

    /**
     * 将列表中下标为"index"位置处的元素替代为"e"
     * @param index 需要被替代元素的下标
     * @param e     新的元素
     * @return      返回被替代的元素
     */
    E set(int index,E e);

    /**
     * 返回列表中下标为"index"位置处的元素
     * @param index 查找元素的"index"元素
     * @return      返回找到的元素
     */
    E get(int index);

    /**
     * 清除列表中所有元素
     * */
    void clear();

    /**
     * 获得迭代器
     * */
    Iterator<E> iterator();
}

3.链表实现细节

　　由于使用java作为实现的语言，因此在设计上参考了jdk自带的链表数据结构：java.util.LinkedList类。

　　LinkedList是一个双端双向链表，因此我们的链表实现也是一个双端双向链表。相比单向链表，双端双向链表功能更加强大，当然也稍微复杂一点。

3.1 链表内部节点

　　双端双向链表内部节点的特点是：每个节点同时拥有该节点"前驱"和"后继"的节点引用(双向)。

　　需要注意的是，对于内部节点两端的引用在不同地方存在着不同称呼。如"前驱(predecess)"/"后继(success)"、"前一个(previous)"/"下一个(next)"、"左(left)/右(right)"等。不必纠结于名词叫法，用自己的方式理解就行。"重要的不是它们叫什么，而是它们是什么"。

　　个人认为"左(left)/右(right)"的称呼比较形象(比较像一群小人，手拉手)，所以在这篇博客中统一使用这种叫法。同时为了描述的简洁，下文中的"链表"默认指的就是"双端双向链表"。

链表内部节点结构示意图：

　　

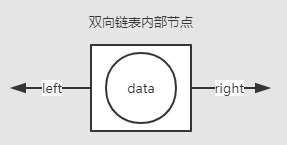
　　在我们的链表实现中，将内部节点抽象为一个私有的静态内部类。首先我们有：

public class LinkedList <E> implements List <E>{
   /**
     * 链表内部节点类
     */
    private static class Node <T>{
        /**
         * 左边关联的节点引用
         * */
        Node<T> left;

        /**
         * 右边关联的节点引用
         * */
        Node<T> right;

        /**
         * 节点存储的数据
         * */
        T data;

        //===================================内部节点 构造函数==================================
        private Node() {}

        private Node(T data) {
            this.data = data;
        }

        /**
         * 将一个节点作为"当前节点"的"左节点" 插入链表
         * @param node  需要插入的节点
         * */
        private void linkAsLeft(Node<T> node){
            //:::先设置新增节点的 左右节点
            node.left = this.left;
            node.right = this;

            //:::将新增节点插入 当前节点和当前节点的左节点之间
            this.left.right = node;
            this.left = node;
        }

        /**
         * 将一个节点作为"当前节点"的"右节点" 插入链表
         * @param node  需要插入的节点
         * */
        private void linkAsRight(Node<T> node){
            //:::先设置新增节点的 左右节点
            node.left = this;
            node.right = this.right;

            //:::将新增节点插入 当前节点和当前节点的左节点之间
            node.right.left = node;
            node.right = node;
        }

        /**
         * 将"当前节点"移出链表
         * */
        private void unlinkSelf(){
            //:::令当前链表的 左节点和右节点建立关联
            this.left.right = this.right;
            //:::令当前链表的 右节点和左节点建立关联
            this.right.left = this.left;

            //:::这样,当前节点就从链表中被移除了(同时,作为私有的内部类,当前节点不会被其它对象引用,很快会被GC回收)
        }
    }
}

　　我们在内部节点类中提供了几个常用的方法，为接下来的链表操作提供基础。

linkAsLeft操作举例说明：

　　已知链表中存在【a，c】两个节点，现在c节点调用linkAsLeft方法，将b节点作为c的左节点插入链表(这时，c节点就是this)。(linkAsRight 原理类似)

linkAsLeft操作示意图：

　　

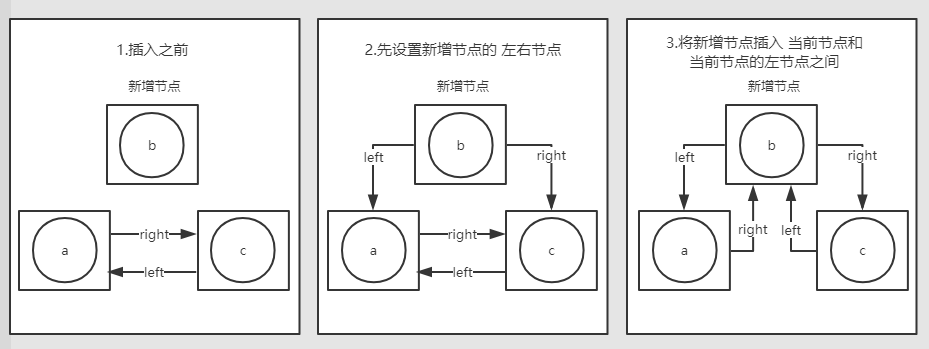
unlinkSelf操作举例说明：

　　已知链表中存在【a，b，c】三个节点，现在b节点调用unlinkSelf方法，将b节点自身移出链表(这时，b节点就是this)。

unlinkSelf操作示意图：

　　

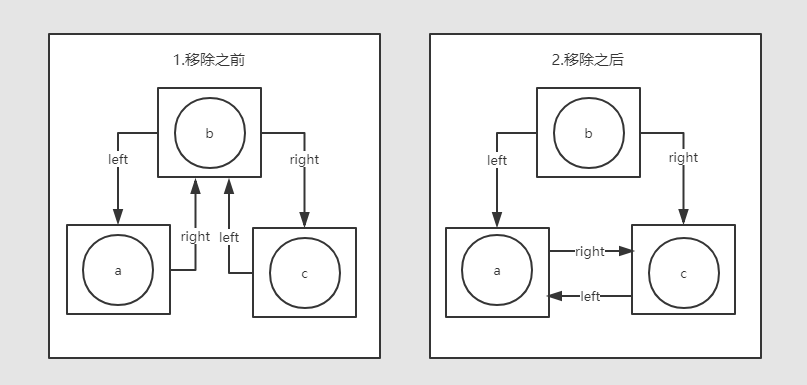
　　可以看到插入和移除操作对于节点左右引用的改变是互逆的。

　　移除操作执行完成后，虽然b节点还持有a，c两节点的引用，但是Node作为封装的私有内部类，可以确保b节点本身不会被其它对象引用，很快会被GC回收。

3.2 链表基本属性

　　链表作为一个数据结构容器，拥有一些必备的属性。

　　链表内部维护着首、尾哨兵两个内部节点(双端)，作为链表的第一个和最后一个节点，新插入的节点总是处于这两个哨兵节点之间，用户也无法感知哨兵节点的存在。哨兵节点并不用于保存数据，其存在的主要目的是为了简化边界条件的逻辑。

　　举个例子：在节点插入时，必须判断当前是否第一个节点，来决定是否需要建立和之前节点的联系；在节点删除时，也必须判断自己的左右节点是否存在，避免空指针异常。首尾哨兵节点的引入使得任何情况下，节点插入，删除时都可以确保其左右节点一定存在，从而避免大量的异常判断。

　　可以看到，哨兵节点的引入简化了代码在边界条件时的各种判断逻辑。这提高了执行效率，更重要的是降低了复杂性，使代码变得更容易理解，也更可靠。

public class LinkedList <E> implements List <E>{
    /**
     * 链表 头部哨兵节点
     * */
    private Node<E> first;
    /**
     * 链表 尾部哨兵节点
     * */
    private Node<E> last;
    /**
     * 链表 逻辑大小
     * */
    private int size;

    public LinkedList() {
        this.first = new Node<>();
        this.last = new Node<>();

        //:::将首尾哨兵节点 进行连接
        this.first.right = this.last;
        this.last.left = this.first;

        //:::初始化size
        this.size = 0;
    }
}

3.3 较为简单的 size()，isEmpty()，indexOf()，contains()方法实现：

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return (this.size == 0);
    }

    @Override
    public int indexOf(E e) {
        //:::当前节点 = 列表头部哨兵
        Node<E> currentNode = this.first;

        if(e != null){
            //:::如果不是查询null元素

            //:::遍历列表
            for(int i=0; i<this.size; i++){
                //:::不断切换当前节点 ==> "当前节点 = 当前节点的右节点"
                currentNode = currentNode.right;
                //:::如果满足要求（注意: equals顺序不能反,否则可能会有currentNode.data为空,出现空指针异常）
                if(e.equals(currentNode.data)){
                    //:::返回下标
                    return i;
                }
            }
        }else{
            //:::如果是查询null元素

            //:::遍历列表
            for(int i=0; i<this.size; i++){
                //:::不断切换当前节点 ==> "当前节点 = 当前节点的右节点"
                currentNode = currentNode.right;
                //:::如果是null元素
                if(currentNode.data == null){
                    //:::返回下标
                    return i;
                }
            }
        }
        //:::遍历列表未找到相等的元素,返回特殊值"-1"代表未找到
        return -1;
    }

    @Override
    public boolean contains(E e) {
        //:::复用indexOf方法,如果返回-1代表不存在;反之,则代表存在
        return (indexOf(e) != -1);
    }

链表 indexOf、contains方法的时间复杂度：　　

　　indexOf方法的实现和向量类似，是通过一次循环遍历来进行查询的，从头部节点不停地跳转到下一个节点，直到发现目标节点或者到达尾部哨兵节点。

　　因此indexOf方法、contains方法的时间复杂度都是O(n)。

3.4 链表增删改查接口实现

3.4.1 下标越界检查

　　链表基于下标的增删改查操作都需要进行下标的越界检查。这里优化了前面"向量篇"博客中提到的缺陷，针对不同的错误，会抛出不同类型的自定义异常，使客户端可以进行更细致的异常处理。

   /**
     * 插入时,下标越界检查
     * @param index 下标值
     */
    private void rangeCheckForAdd(int index){
        //:::如果大于size的值,抛出异常
        //:::注意：插入时,允许插入线性表的末尾,因此(index == size)是合法的
        if(index > this.size){
            throw new OutOfIndexBoundException("index error  index=" + index + " size=" + this.size) ;
        }
        if(index < 0){
            throw new NegativeOfIndexException("index error  index=" + index + " size=" + this.size) ;
        }
    }

    /**
     * 下标越界检查
     * @param index 下标值
     */
    private void rangeCheck(int index){
        //:::如果大于等于size的值,抛出异常
        if(index >= this.size){
            throw new OutOfIndexBoundException("index error  index=" + index + " size=" + this.size) ;
        }
        if(index < 0){
            throw new NegativeOfIndexException("index error  index=" + index + " size=" + this.size) ;
        }
    }

　　同时，链表基于下标的操作都需要先查询出下标对应的内部节点，通过操纵对应的内部节点来进行相关操作。因此需要抽象出一个通用的查询方法。

   /**
     * 返回下标对应的 内部节点
     * */
    private Node<E> find(int index){
        //:::要求调用该方法前,已经进行了下标越界校验
        //:::出于效率的考虑,不进行重复校验

        //:::判断下标在当前列表的大概位置（前半段 or 后半段）尽量减少遍历查询的次数
        if(index < this.size/2){
            //:::下标位于前半段

            //:::从头部结点出发,进行遍历(从左到右)
            Node<E> currentNode = this.first.right;
            //:::迭代(index)次
            for(int i=0; i<index; i++){
                currentNode = currentNode.right;
            }

            return currentNode;
        }else{
            //:::下标位于后半段

            //:::从尾部结点出发,进行遍历(从右到左)
            Node<E> currentNode = this.last.left;
            //:::迭代(size-index-1)次
            for(int i=index; i<size-1; i++){
                currentNode = currentNode.left;
            }
            return currentNode;
        }
    }

find方法的时间复杂度 :

　　可以看到，find方法会根据下标所处的大概位置决定开始遍历的方向(尽量减少迭代查询的次数)，下标越接近头部或者尾部，查询次数越少。因此下标在靠近头部、尾部时效率较高，而在居中位置效率较低。

　　从概率的角度上来看，下标访问是随机的，因此find方法的时间复杂度被认为是O(n)。

3.4.2 链表的插入方法实现

    @Override
    public boolean add(E e) {
        //:::将新的数据 插入到列表末尾 ==> 作为last节点的前一个节点插入
        this.last.linkAsLeft(new Node<>(e));
        //:::size自增
        this.size++;

        return true;
    }

    @Override
    public void add(int index, E e) {
        //:::插入时,下标越界检查
        rangeCheckForAdd(index);

        //:::查询出下标对应的 目标节点
        Node<E> targetNode = find(index);

        //:::将新的数据节点 作为目标节点的前一个节点插入
        targetNode.linkAsLeft(new Node<>(e));

        //:::size自增
        this.size++;
    }

插入方法的时间复杂度:

尾部插入：

　　尾部插入方法中，由于我们维护了一个last哨兵节点，通过直接将新节点插入last哨兵的左边，完成尾部数据的插入。

　　因此，尾部插入方法的时间复杂度为O(1)。

下标插入：

　　下标插入方法中，依赖find方法查询出下标对应的节点，然后将新节点进行插入。

　　因此，下标插入方法的时间复杂度为O(n)；对于头部，尾部节点的插入，时间复杂度为O(1)。

3.4.3 删除方法的实现

    @Override
    public boolean remove(E e) {
        //:::当前节点 = 列表头部哨兵
        Node<E> currentNode = this.first;
        if(e != null){
            //:::如果不是查询空元素
            //:::遍历列表
            for(int i=0; i<this.size; i++){
                //:::不断切换当前节点 ==> "当前节点 = 当前节点的右节点"
                currentNode = currentNode.right;
                //:::如果满足要求（注意: equals顺序不能反,否则可能出现currentNode.data为空,出现空指针异常）
                if(e.equals(currentNode.data)){
                    //:::匹配成功,将当前节点从链表中删除
                    currentNode.unlinkSelf();
                    //:::删除成功,返回true
                    return true;
                }
            }
        }else{
            //:::如果是查询null元素
            //:::遍历列表
            for(int i=0; i<this.size; i++){
                //:::不断切换当前节点 ==> "当前节点 = 当前节点的右节点"
                currentNode = currentNode.right;
                //:::如果满足要求
                if(currentNode.data == null){
                    //:::匹配成功,将当前节点从链表中删除
                    currentNode.unlinkSelf();
                    //:::删除成功,返回true
                    return true;
                }
            }
        }
        //:::遍历列表未找到相等的元素,未进行删除 返回false
        return false;
    }

    @Override
    public E remove(int index) {
        //:::下标越界检查
        rangeCheck(index);

        //:::获得下标对应的 Node
        Node<E> targetNode = find(index);

        //:::将目标节点从链表中移除
        targetNode.unlinkSelf();
        //:::size自减
        this.size--;

        //:::返回被移除的节点data值
        return targetNode.data;
    }

删除方法的时间复杂度:

特定元素删除：

　　链表特定元素的删除和find方法类似，通过一次遍历获得目标节点，然后进行删除。

　　因此，特定元素的删除方法时间复杂度为O(n)。

下标删除：

　　下标删除方法中，依赖find方法查询出下标对应的节点，然后将目标节点进行删除。

　　因此，下标删除方法的时间复杂度为O(n)；对于头部，尾部节点的删除，时间复杂度为O(1)。

3.4.4 修改/查询方法实现

    @Override
    public E set(int index, E e) {
        //:::下标越界检查
        rangeCheck(index);

        //:::获得下标对应的 Node
        Node<E> targetNode = find(index);

        //:::先暂存要被替换的"data"
        E oldValue = targetNode.data;
        //:::将当前下标对应的"data"替换为"e"
        targetNode.data = e;

        //:::返回被替换的data
        return oldValue;
    }

    @Override
    public E get(int index) {
        //:::下标越界检查
        rangeCheck(index);

        //:::获得下标对应的 Node
        Node<E> targetNode = find(index);

        return targetNode.data;
    }

修改/查询方法的时间复杂度：

　　可以看到，链表基于下标的修改和查询都依赖于find方法。

　　因此，修改/查询方法的时间复杂度为O(n)；对于头部，尾部节点的修改和查询，时间复杂度为O(1)。

3.5 链表其它接口

3.5.1 clear方法

　　clear方法用于清空链表内的元素，初始化链表。

    @Override
    public void clear() {
        //:::当头部哨兵节点不和尾部哨兵节点直接相连时
        while(this.first.right != this.last){
            //:::删除掉头部哨兵节点后的节点
            remove(0);
        }

        //:::执行完毕后,代表链表被初始化,重置size
        this.size = 0;
    }

3.5.2 toString方法

    @Override
    public String toString() {
        Iterator<E> iterator = this.iterator();

        //:::空列表
        if(!iterator.hasNext()){
            return "[]";
        }

        //:::列表起始使用"["
        StringBuilder s = new StringBuilder("[");

        //:::反复迭代
        while(true){
            //:::获得迭代的当前元素
            E data = iterator.next();

            //:::判断当前元素是否是最后一个元素
            if(!iterator.hasNext()){
                //:::是最后一个元素，用"]"收尾
                s.append(data).append("]");
                //:::执行完毕 返回拼接完成的字符串
                return s.toString();
            }else{
                //:::不是最后一个元素
                //:::使用", "分割，拼接到后面
                s.append(data).append(", ");
            }
        }
    }

　　链表的toString方法在之前"向量篇"的基础上进行了优化。基于列表List的Iterator接口进行遍历，实现了同样的功能。事实上，改进之后的toString方法也同样可以适用于向量。

　　在jdk的Collection框架中，框架设计者要求所有的单值数据结构容器都必须实现Iterator接口，因而将toString方法在AbstractCollection这一顶层抽象类中进行了实现，达到统一单值数据结构容器toString方法默认行为的目的，增强了代码的可重用性。

4.链表的Iterator(迭代器)

   /**
     * 链表迭代器实现
     * */
    private class Itr implements Iterator<E>{
        /**
         * 当前迭代器光标位置
         * 初始化指向 头部哨兵节点
         * */
        private Node<E> currentNode = LinkedList.this.first;
        /**
         * 最近一次迭代返回的数据
         * */
        private Node<E> lastReturned;

        @Override
        public boolean hasNext() {
            //:::判断当前节点的下一个节点 是否是 尾部哨兵节点
            return (this.currentNode.right != LinkedList.this.last);
        }

        @Override
        public E next() {
            //:::指向当前节点的下一个节点
            this.currentNode = this.currentNode.right;

            //:::设置最近一次返回的节点
            this.lastReturned = currentNode;

            //:::返回当前节点的data
            return this.currentNode.data;
        }

        @Override
        public void remove() {
            if(this.lastReturned == null){
                throw new IteratorStateErrorException("迭代器状态异常: 可能在一次迭代中进行了多次remove操作");
            }

            //:::当前光标指向的节点要被删除,先暂存引用
            Node<E> nodeWillRemove = this.currentNode;

            //:::由于当前节点需要被删除,因此光标前移,指向当前节点的上一个节点
            this.currentNode = this.currentNode.left;

            //:::移除操作需要将最近一次返回设置为null，防止多次remove
            this.lastReturned = null;

            //:::将节点从链表中移除
            nodeWillRemove.unlinkSelf();
        }
    }

　　迭代器在实现时需要满足接口的行为定义，remove方法在一次next迭代中不能被重复调用，否则会产生古怪的异常。

5.链表性能

　　链表作为线性表的一种，一般被用来和同为线性表的向量进行比较。

空间效率：

　　比起向量，链表的单位数据是存储在内部节点之中的。而内部节点除了含有数据域，还包括了左右节点的引用，因此链表的空间效率比向量稍差。

时间效率：

　　在有些书籍或者博客中会笼统地介绍："比起向量，链表的插入，删除操作时间复杂度较低(向量O(n)，链表O(1))；查询，修改操作时间复杂度较高(向量O(1)，链表O(n))"。

　　链表插入，删除操作的时间复杂度本身确实是O(1)(仅需要修改节点引用)，因为不用和向量一样批量的移动内部元素。

　　但是需要注意的是，由于我们对链表进行了封装，客户端无法感知到内部节点的存在，因此也就无法获取到内部节点的引用。所以，链表的插入，删除操作其实并不纯粹，而总是会伴随着基于下标的随机访问或者特定元素的查找，这会把大量的时间消耗在遍历查询中。

　　总体来说：

　　1. 链表的增加、删除操作在头部、尾部的执行由于避免了大量的查询，因此效率非常高(时间复杂度为O(1))。但是在链表较为居中位置的执行效率却不尽如人意(时间复杂度为O(n))。

　　2. 链表的随机修改、查询操作，其时间复杂度为O(n)。相比向量，链表随机查询、修改的效率较差。

　　针对链表的上述特性可以发现，许多只在头尾处频繁操作的场合，链表的表现很好，可以考虑通过链表来实现(例如：栈，队列等)。　

6.链表总结

　　到这里，我们已经完成了一个很基础的链表数据结构。虽然比较简单，但已经有一个基本的框架，读者完全可以在理解思路的基础之上进行各个维度的优化。

　　链表作为基础的数据结构之一，其原理是值得学习和了解的。因为，许多算法和高级的数据结构都依赖于链表或者链表的其它变种实现(跳跃表等)；其次链表这种"将数据存放在节点中，并且维护节点之间关系"的设计思想也存在于很多高级数据结构之中(树、图等)，对链表的掌握是理解一些更复杂数据结构的基础。

　　代码在我的 github上：https://github.com/1399852153/DataStructures，这篇文章还存在许多不足之处，请多指教。