FFT与一些冷门问题

FFT也能用于一些特殊的字符串匹配与最小化问题。

Prob 1 : 给出模式串A与文本串B，两个串中只有26个大写字母与通配符'?'（即可以任意匹配一个字符），求A在B中的匹配数。要求以FFT为例给出上限为O(nlogn)的算法。

Prob 2 : 给出模式串A与文本串B，字符集很小，求A在B中的匹配数，允许有k个字符不同。要求以FFT为例给出上限为O（nlogn*|S|）的算法。

Prob 3 : 给出数列a和b，长度均为n，a可以顺时针转动但不能翻转，最小化sigma(ai*bi)。要求以FFT为例给出上限为O（nlogn）的算法。

---

不知道是什么东西的引导

我们先看看FFT干了什么，就是个卷积。

以数组a和b为例（这里下标从1开始），a有4位，b有8位，卷出的结果放在c数组中。

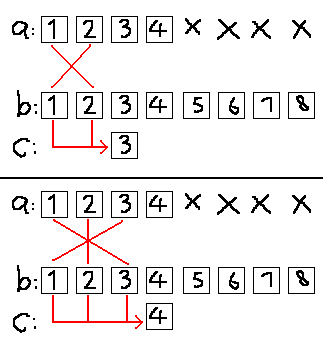
然而并没有什么用处。我们再往后看几位：

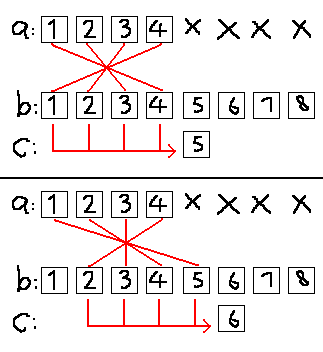
虽然FFT时会把a数组给自动补全，但从实际意义上来讲，只是整个a数组与b数组中四个数相乘放进c中。

不难发现，此时的下标就是一个“占位符”。

我们顺便把a数组反一反，就有：

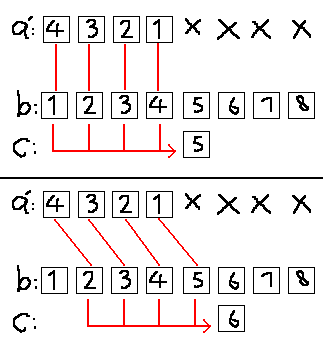
这样就有很好的性质了，c数组中从第5位开始，每往后一位就是整个a数组与b数组中连续的四位积的和。

同样可以拓展到更大的数组中，接下来的题目就要利用这个特点。

---

Prob 1

我们发现字符串的匹配很类似于上述图片中一位位算过去。

先不考虑通配符，只是普通的字符串匹配。定义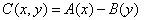为A的第x位与B的第y位的匹配度。若C为0，则是匹配的。

再定义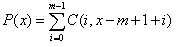，表示B字符串中以x为结尾，向前m-1位与A字符串的匹配度。我们天真地考虑若P为0，则是匹配的。

但是C有正有负，因此一旦连续的几位的可重集是相同的，P的结果就为0。

所以在C上动手脚。干脆加个平方吧：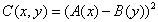

这样，

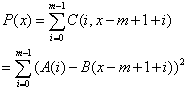
但还不能优化！因此我们又看了看上面的图，把A字符串反了过来。定义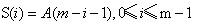

则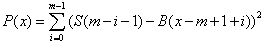

注意到(m-i-1)+(x-m+1+i)==x，有：

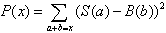
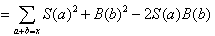
这样S与B做一遍卷积就行了。S与B的值取字符串的字符值就行了。

那带上通配符，只要有任何字符遇上“?”，C的值就必须是0。这样在原来P的式子中，后面乘上S与B中相应的第几位，若是“?”，给其赋值为0。则

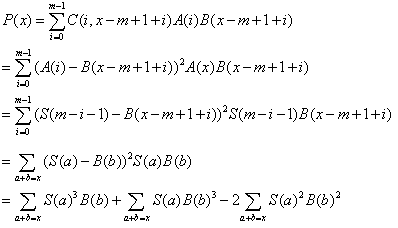
做三次FFT，加起来等于0的，即为匹配。

 //源：https://www.luogu.org/problemnew/show/P4173
 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=;
 const double pi=3.1415926535898;
 struct com
 {
     double a,b;
     com(double A=,double B=){a=A,b=B;}
     void operator=(com x){a=x.a,b=x.b;}
     com operator+(com x){return com(a+x.a,b+x.b);}
     com operator-(com x){return com(a-x.a,b-x.b);}
     com operator*(com x){return com(a*x.a-b*x.b,a*x.b+b*x.a);}
     com operator/(double d){return com(a/d,b/d);}
     com operator*(double d){return com(a*d,b*d);}
 }A[maxn],B[maxn],ans[maxn];
 int n,m,limit,r[maxn],len,g1[maxn],g2[maxn];
 char ch;
 int re(int x)
 {
     int sum=;
     for(int i=;i<len;++i)
     {
         sum=sum*+x%;
         x/=;
     }
     return sum;
 }
 void FFT(com*A,int g)
 {
     for(int i=;i<limit;++i)
         if(i<r[i])swap(A[i],A[r[i]]);
     for(int i=;i<=limit;i*=)
     {
         com w(cos(*pi/i),g*sin(*pi/i));
         for(int j=;j<limit/i;++j)
         {
             com d(,);
             for(int k=;k<i/;++k)
             {
                 com a=A[i*j+k],b=d*A[i*j+i/+k];
                 A[i*j+k]=a+b;
                 A[i*j+i/+k]=a-b;
                 d=w*d;
             }
         }
     }
 }
 void out(com*A)
 {
     for(int i=;i<limit;++i)cout<<A[i].a<<' ';
     cout<<endl;
 }
 void get(com*A,com*B)
 {
     FFT(A,);
     FFT(B,);
     for(int i=;i<limit;++i)A[i]=A[i]*B[i];
     FFT(A,-);
     for(int i=;i<limit;++i)A[i]=A[i]/limit;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n>>m;
     for(int i=n-;i>=;--i)
     {
         cin>>ch;
         if(ch!='*')
         {
             int x=ch-'a'+;
             A[i]=g1[i]=x;
         }
     }
     for(int i=;i<m;++i)
     {
         cin>>ch;
         if(ch!='*')
         {
             int x=ch-'a'+;
             g2[i]=x;
             B[i]=x*x*x;
         }
     }
     limit=;
     while(limit<n+m+)limit*=,++len;
     for(int i=;i<limit;++i)r[i]=re(i);
     get(A,B);
     for(int i=;i<limit;++i)ans[i]=A[i];

     for(int i=limit-;i>=;--i)A[i]=g1[i]*g1[i]*g1[i];
     for(int i=;i<limit;++i)B[i]=g2[i];
     get(A,B);
     for(int i=;i<limit;++i)ans[i]=ans[i]+A[i];

     for(int i=limit-;i>=;--i)A[i]=g1[i]*g1[i];
     for(int i=;i<limit;++i)B[i]=g2[i]*g2[i];
     get(A,B);
     for(int i=;i<limit;++i)ans[i]=ans[i]-A[i]*;

     int tot=;
     for(int i=n-;i<m;++i)if(int(ans[i].a+0.5)==)++tot;
     cout<<tot<<endl;
     for(int i=n-;i<m;++i)if(int(ans[i].a+0.5)==)cout<<i-n+<<' ';
     cout<<endl;
     return ;
 }

代码

---

Prob 2

若字符只有’0'和'1'的呢？按照上面的做法，最后结果小于等于2的即为匹配（因为会有地方算两遍）。

再拓展一下，字符集多大就做几遍。最后的和加起来即可。

但由于一些奇妙的原因，至今我交不过去。只有网址。

其实随便哈希就能过了，SA也行。

https://www.luogu.org/problemnew/show/P3763

---

Prob 3

仍然是老套路。我们只要把其中某个数组的长度变为两倍，再重复写下前面的数就行了。

类似的题目：https://www.luogu.org/problemnew/show/P3723

最后，如果能用一些数据结构或方法来维护的话就别写FFT了。