PNPoly算法代码例子，判断一个点是否在多边形里面

写C语言的实验用到的一个算法，判断一个点是否在多边形的内部。C的代码如下：

int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
      (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) /
      (verty[j]-verty[i]) + vertx[i]) )
      c = !c;
    }
  return c;
}

其中nvert是多边形顶点的个数，vertx和verty分别是多边形顶点横、纵坐标的数组，textx和testy是待测点的坐标。这个算法是由W. Randolph Franklin提出的，根据Jordan curve theorem，多边形将平面分为内外两个区域，假设待测点在多边形内部，从待测点引出一条射线必然会与多边形有至少一个交点。该射线与多边形第一次相交时将“冲出”多边形，第二次相交将“进入”多边形，依此类推，若射线与多边形有奇数个交点，则该点在多边形内部，反之则在外部。

PNPoly算法正是从待测点引出一条水平向右的射线，并计算与多边形的交点个数。解释一下这段代码：for (i = 0, j = nvert-1; i < nvert; j = i++)循环的含义就是始终让j = i – 1，如果i = 0那么j = nvert – 1，从而依次检验多边形的每条边。接下来的重点就是条件语句，(verty[i]>testy) != (verty[j]>testy)很好理解，就是一条边上的两个顶点分别在待测点的上方和下方，通过这条语句可以知道从待测点向右引出的射线有可能与该条边相交（只要待测点在边的左侧即可）。

但具体判断相交就要交给解析几何了。建系写出该条边所在直线的方程：

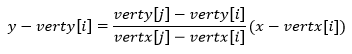
变形一下：

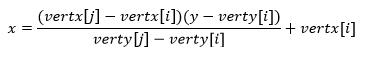
代入待测点坐标，根据图形关系得到这个不等式：

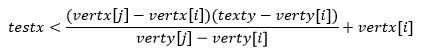
也就是语句testx < vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]了.