CF-1440C2 Binary Table (Hard Version) （构造，模拟）

Binary Table (Hard Version)

题意

\(n*m(2\le n,m\le 100)\) 的01矩阵，每次可以选择一个宽度为2的子矩阵，将四个位置中的任意3个进行翻转，即0变1,1变0。要求构造操作次数小于 \(n*m\) 的方案，使得该矩阵最终变成一个全0矩阵。

分析

构造方法可能有很多种，只要能够满足题意即可。

从第一行开始到倒数第三行，逐列扫描，假设当前扫描的位置为 (i,j)，且当前位置为1，那么执行操作一或者操作二。\(i\le n-2\) ，只扫描前 \(n-2\) 行，最后空下两行特殊处理。这之前的 \((n-2)*m\) 个位置，总共使用了不超过 \((n-2)*m\) 次操作。

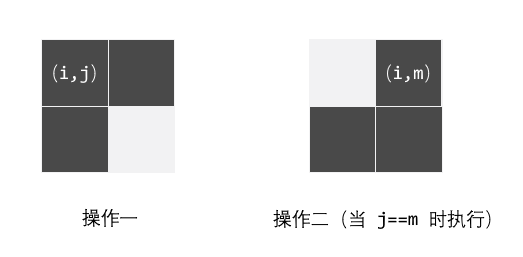
处理最后两行时，需要4个一组进行处理。分情况讨论

1. 如果 4 个都是 ‘1’ ，进行一次翻转，只留右下角的 1，这个 1 留到最后处理

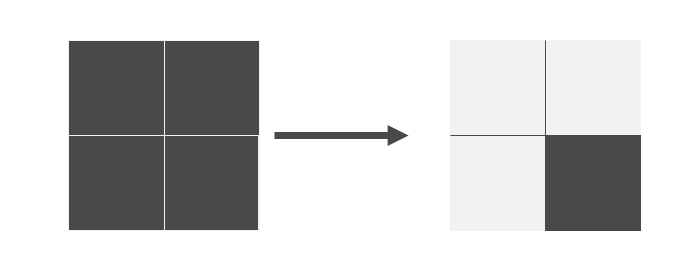
1. 如果有某 3 个是 ‘1’ ，那么一次操作可以搞定

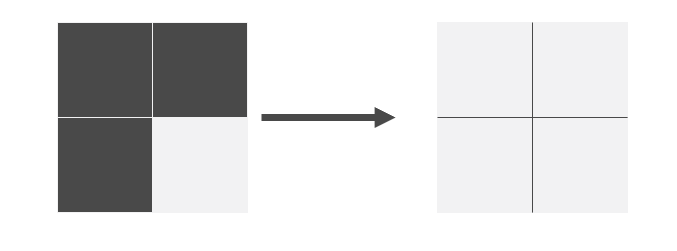
1. 如果有某 2 个是 '1'，那么可以细分为两种情况，这两种情况都可以用两步解决

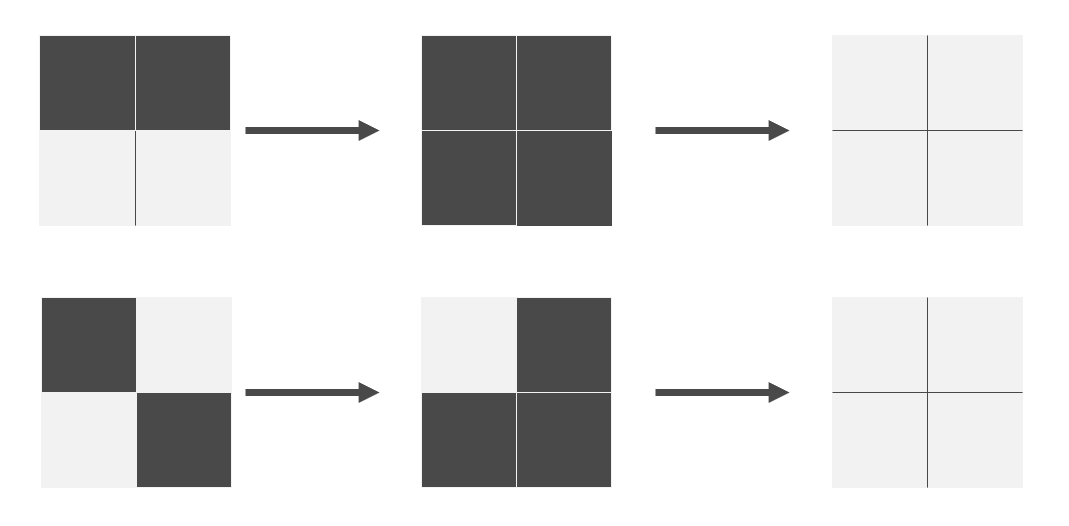
1. 如果只有 1 个是 '1'，那么留作最后考虑。

根据上面的情况，对最后两行进行处理，如果 \(m\) 是偶数，刚好可以处理完。但如果 \(m\) 是奇数，那么对于最后一列的两个格子，我们需要特殊考虑。

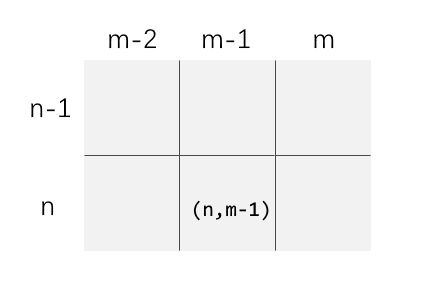
可以想到，我们按照 4 个一组处理完左边四个之后，最多只会在 (n,m-1) 这个位置留一个 1，那么不论第 m 列是什么情况，我们都可以在两步操作内，将他们变为0。这个操作是绝对保险的。

最后，只剩下最后两行的某些单独的 1 了，这些单独的 1 可以在 3 步内消除，至于为什么这么操作不会使得操作次数爆炸，可以从这些 1 的产生来源考虑。

1. 这个 1 原本就摆在这里，那么旁边 3 个空位之前是没有操作过的，这就给这个 1 留下了多余的操作空间。

2. 这个 1 是消了 3 个之后剩下的，那么消除那 3 个用了一次，消除单独的 1 用了 3 次，刚好四次。

3. 对于 m 为奇数时，最右边一列中单独的 1，这个虽然也需要使用 3 步，但是由于此时 m-1 列都是空的，这得多亏左边那四个之前是消除干净了的。而 4 个一组消除干净最多只需要两步，所以这种情况也是保险的。
   
   

#include <bits/stdc++.h>
using namespace std;
const int N = 101;
int T, n, m, t[N][N];
char s[N][N];
vector<pair<int,int> > v;
void add(int x, int y){
    v.push_back({x, y});
    t[x][y] ^= 1;
}
void add(int x, int y, int p){
    if(p == 0) add(x, y);
    else if(p == 1) add(x, y+1);
    else if(p == 2) add(x+1, y);
    else if(p == 3) add(x+1, y+1);
}
void solve(int x, int y){
    int c0 = t[x][y];
    int c1 = t[x][y+1];
    int c2 = t[x+1][y];
    int c3 = t[x+1][y+1];
    int c = c0 + c1 + c2 + c3;
    if(c == 4) {
        add(x, y, 0);
        add(x, y, 1);
        add(x, y, 2);
    } else if(c == 3) {
        if(c0 == 0) add(x, y, 1), add(x, y, 2), add(x, y, 3);
        if(c1 == 0) add(x, y, 0), add(x, y, 2), add(x, y, 3);
        if(c2 == 0) add(x, y, 0), add(x, y, 1), add(x, y, 3);
        if(c3 == 0) add(x, y, 0), add(x, y, 1), add(x, y, 2);
    } else if(c == 2){
        if(c0 && c1) {
            add(x, y, 0);add(x, y, 2);add(x, y, 3);
            add(x, y, 1);add(x, y, 2);add(x, y, 3);
        } else if(c0 && c2) {
            add(x, y, 0);add(x, y, 1);add(x, y, 3);
            add(x, y, 2);add(x, y, 1);add(x, y, 3);
        } else if(c0 && c3) {
            add(x, y, 0);add(x, y, 1);add(x, y, 2);
            add(x, y, 3);add(x, y, 1);add(x, y, 2);
        } else if(c1 && c2){
            add(x, y, 1);add(x, y, 0);add(x, y, 3);
            add(x, y, 2);add(x, y, 0);add(x, y, 3);
        } else if(c1 && c3) {
            add(x, y, 1);add(x, y, 0);add(x, y, 2);
            add(x, y, 3);add(x, y, 0);add(x, y, 2);
        } else if(c2 && c3) {
            add(x, y, 2);add(x, y, 0);add(x, y, 1);
            add(x, y, 3);add(x, y, 0);add(x, y, 1);
        }
    }
}
int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d%d", &n, &m);
        for(int i=1;i<=n;i++) scanf("%s", s[i]+1);
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                t[i][j] = s[i][j] - '0';
            }
        }
        for(int i=1;i<=n-2;i++){
            for(int j=1;j<=m;j++){
                if(t[i][j] == 0) continue;
                add(i, j); add(i+1, j);
                if(j == m) add(i+1, j-1);
                else add(i, j+1);
            }
        }
        for(int j = 1; j + 1 <= m; j += 2){
            solve(n - 1, j);
        }
        if(m & 1) solve(n - 1, m - 1);
        // 处理倒数第二行中单着的
        for(int j = 1; j <= m; j++){
            if(t[n-1][j] == 0) continue;
            if(j == m) {
                add(n-1, j-1, 1); add(n-1, j-1, 0); add(n-1, j-1, 3);
                add(n-1, j-1, 0); add(n-1, j-1, 2); add(n-1, j-1, 1);
                add(n-1, j-1, 3); add(n-1, j-1, 2); add(n-1, j-1, 1);
            } else {
                add(n-1, j, 0); add(n-1, j, 1); add(n-1, j, 2);
                add(n-1, j, 2); add(n-1, j, 0); add(n-1, j, 3);
                add(n-1, j, 1); add(n-1, j, 0); add(n-1, j, 3);
            }
        }
        // 处理倒数第一行单着的
        for(int j = 1; j <= m; j++){
            if(t[n][j] == 0) continue;
            if(j == m) {
                add(n-1, j-1, 3); add(n-1, j-1, 2); add(n-1, j-1, 1);
                add(n-1, j-1, 2); add(n-1, j-1, 0); add(n-1, j-1, 3);
                add(n-1, j-1, 1); add(n-1, j-1, 0); add(n-1, j-1, 3);
            } else {
                add(n-1, j, 2); add(n-1, j, 0); add(n-1, j, 3);
                add(n-1, j, 0); add(n-1, j, 1); add(n-1, j, 2);
                add(n-1, j, 3); add(n-1, j, 1); add(n-1, j, 2);
            }
        }
        cout << v.size() / 3 << endl;
        for(int i=0;i<v.size();){
            #define x first
            #define y second
            printf("%d %d %d %d %d %d\n", v[i].x, v[i].y, v[i+1].x, v[i+1].y, v[i+2].x, v[i+2].y);
            i += 3;
        }
        v.clear();
    }
    return 0;
}