[Fundamental of Power Electronics]-PART I-5.不连续导电模式-5.1 DCM来源和模式边界

引子：

当使用电流单向和/或电压单向半导体开关实现DC-DC变换器的理想开关时，可能会出现一种或多种被称为不连续导电模式(DCM)的新工作模式。当电感电流或电容电压的纹波大到足以导致所施加的开关电流或电压极性反转时，出现的不连续导通的模式，从而这违反了使用半导体器件实现开关时所做出的的电流或者电压单向的假设。DCM通常出现在DC-DC变换器和整流器中，有时也会出现在逆变器或者其他包含两象限开关的变换器中。

DCM通常发生在轻载工作且包含电流单向开关的变换器中，电感电流纹波较大。由于通常要求变换器在轻载的情况下工作，因此经常会遇到DCM。事实上，有些变换器专门设计为在所有负载下以DCM工作。

变换器的性质在DCM下发生了根本变化。变换比M变得依赖于负载，并且输出阻抗增加。负载减轻或者去除时，输出控制可能会失效。我们将在后面的章节中看到，变换器的动态特性也发生了显著变化。

本章解释了DCM的起源，并推导出了模式边界。还描述了用于解决变换器波形和输出电压的技术。不管工作模式如何，电感伏秒平衡和电容电荷平衡的原理在稳态下必须始终正确。然而，应用小纹波近似需要一定的谨慎，因为电感电流纹波(或电感电流或电容电压纹波之一)并不小。

以Buck和Boost变换器为例进行求解。基本降压、升压和降压升压转换器的特性以表格形式总结。

5.1 DCM来源和模式边界

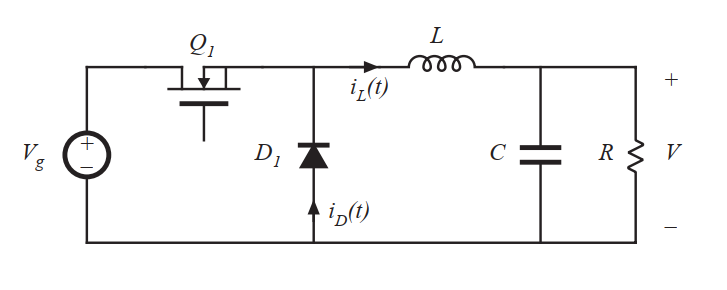
Fig 5.1 Buck converter example

让我们考虑电感和开关电流波形如何随着负载功率的降低而变化。让我们以图5.1所示的Buck变换器作为一个简单的例子。连续模式下的电感电流\(i_{L}(t)\)和二极管电流波形如图5.2所示。正如第二章所述，电感电流\(i_{L}(t)\)包含一个直流分量\(I\)，加上一个峰值为\(\Delta i_{L}\)的开关纹波。在第二个子间隔内，二极管的电流等于电感电流。在此期间，二极管的最小电流为\((I-\Delta i_{L})\)。而二极管是单象限开关器件，工作在CCM下需要电流恒为正值。在第二章中，电感电流的直流分量\(I\)等于负载电流：

\[I=\frac{V}{R} \tag{5.1}
\]

由于没有直流电流流过电容C，可以看做电流\(I\)取决于负载电阻\(R\)。开关纹波的幅值为：

\[\Delta i_{L}=\frac{(V_{g}-V)}{2L}DT_{s}=\frac{V_{g}DD^{'}T_{s}}{2L} \tag{5.2}
\]

纹波电流幅值取决于电压\((V_{g}-V)\)，电感\(L\)以及晶体管导通时间\(DT_{s}\)。但是它并不取决于负载电阻\(R\)。电感电流纹波随电压变化而不是电流。

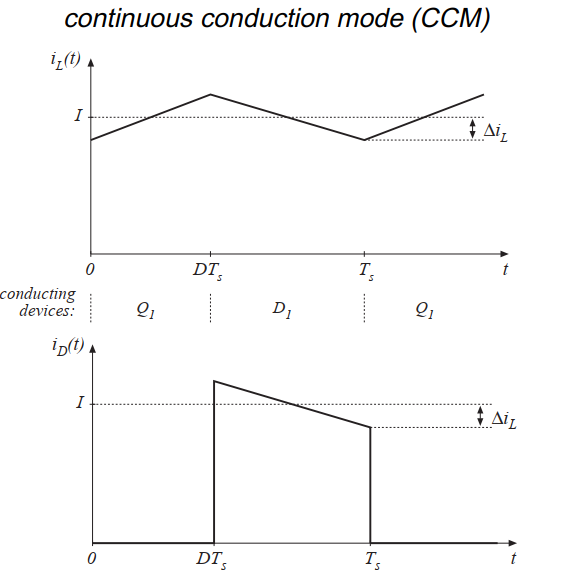
Fig 5.2 Buck converter waveforms in the continuous conduction mode: inductor current and diode current.

假设现在负载电阻\(R\)增加，因此直流负载电流减小。电感电流的直流分量\(I\)也会减小，但纹波电流幅值\(\Delta i_{L}\)不会变化。如果我们持续增加\(R\)，如图5.3所示，直至工作点达到\(I=\Delta i_{L}\)。可以看到，在开关周期最后时刻，电感电流\(i_{L}(t)\)和二极管电流\(i_{D}(t)\)均为0。而此时负载电流依然是正的且非零。

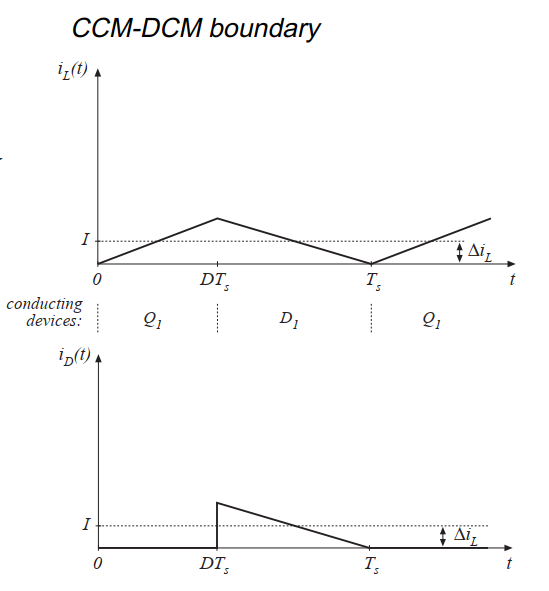
Fig 5.3 Buck converter waveforms at the boundary between the continuous and discontinuous conduction modes: inductor current and diode current

当我们继续增加电阻\(R\)会发生什么？二极管电流是不可能为负值的；因此，在开关周期结束前，二极管必定是反向偏置的。如图5.4所示，在每个开关周期\(T_{s}\)内，有三个间隔区间。在第一个间隔为\(D_{1} T_{s}\)的区间，晶体管导通，在第二个间隔为\(D_{2} T_{s}\)的区间，二极管导通。在第二个区间结束后，二极管电流变为0，在开关周期的剩余时间里，二极管和晶体管都不会导通。此时变换器就是工作在不连续导电模式(DCM)。

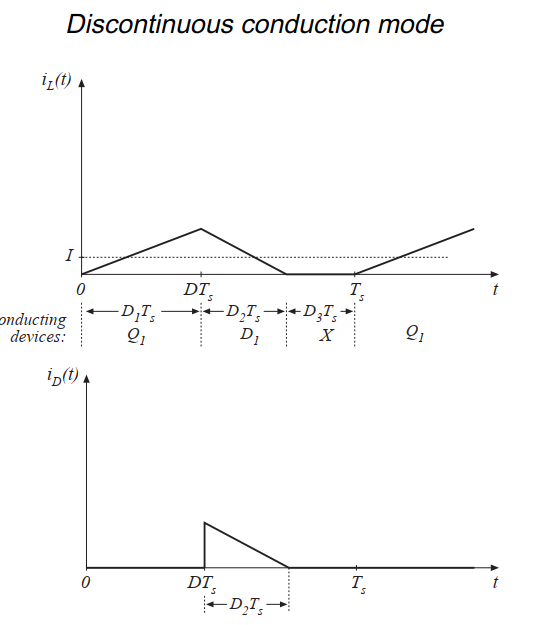
Fig 5.4 Buck converter waveforms in the discontinuous conduction mode: inductor current and diode current.

图5.3给出了一种寻找连续和不连续导电模式边界的方法。可以看出，对于该Buck变换器示例，二极管电流在整个区间\(DT_{s}<t<T_{s}\)上为正的条件是\(I>\Delta i_{L}\)。因此工作在CCM和DCM的条件为：

\[I>\Delta i_{L} (for CCM) \\
I<\Delta i_{L} (for DCM) \tag{5.3}
\]

其中\(I\)和\(\Delta i_{L}\)是在假设变换器工作在CCM下得到的。将式(5.1)和(5.2)代入式(5.3)得到如下所示的DCM工作的条件：

\[\frac{D V_{g}}{R} <\frac{D D^{'} T_{s} V_{g}}{2L} \tag{5.4}
\]

简化公式：

\[\frac{2L}{R T_{s}}<D^{'} \tag{5.5}
\]

同样可以表示为

\[K<K_{crit}(D)--for DCM \tag{5.6}
\]

其中\(K=2L/(RT_{s})\)，并且\(K_{crit}(D)=D^{'}\)。

无量纲参数K是变换器以不连续导电模式运行的趋势的量度。K值大导致CCM运行，而对于某些占空比值，K值小导致DCM运行。不同模式间的临界值\(K_{crit}(D)\)是占空比的函数，对于Buck变换器而言，他等于\(D^{'}\)。

临界值\(K_{crit}(D)\)与占空比之间关系图如图5.5所示。并且任意选择了一个\(K\)作为示例。对于图中所示的值，可以看出变换器在低占空比时工作在DCM，在高占空比时工作在CCM。图5.6说明了重载的情况。负载电阻R的值减小，使得K更大。如果K大于1，则变换器在所有占空比下都以CCM工作。

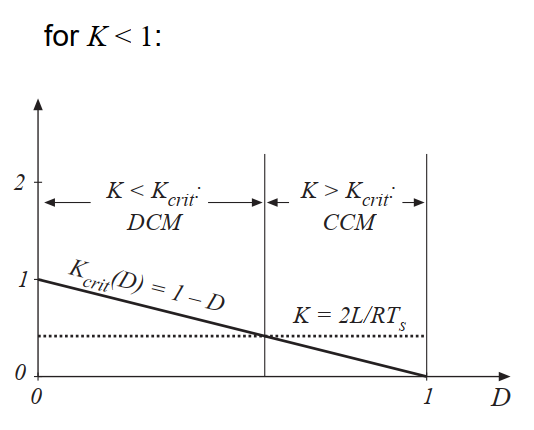
Fig 5.5 Buck converter \(K_{crit}(D)\) vs \(D\). The converter operates in CCM when \(K>K_{crit}\)，and in DCM when \(K<K_{crit}\)

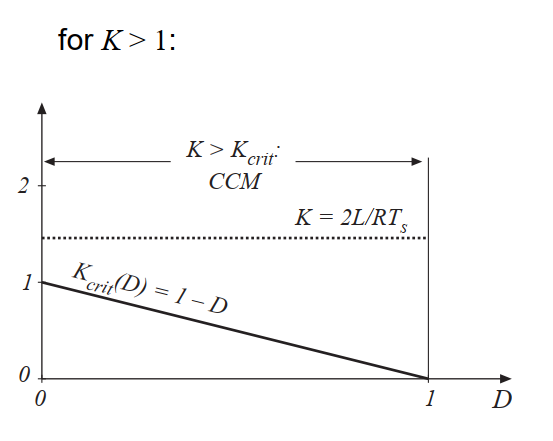
Fig 5.6 Comparison of \(K\) with \(K_{crit}(D)\)，for a larger value of \(K\). Since \(K>1\)，the converter operates in the CCM for all \(D\).

那么就可以很自然的用负载电阻\(R\)而非无量纲参数\(K\)来表示工作模式的边界。式(5.6)可以重新调整，直接揭示工作模式边界对负载电阻的依赖性:

\[R<R_{crit}(D)--for CCM \\R>R_{crit}(D)--for DCM \tag{5.7}
\]

其中

\[R_{crit}(D)=\frac{2L}{D^{'}T_{s}}
\]

因此，当负载电阻\(R\)超过临界值\(R_{crit}\)时，变换器进入DCM。这个临界值取决于电感值，开关周期和占空比。注意，由于\(D^{'} \leq 1\)，\(R_{crit}\)的最小值是\(2L/T_{s}\)。因此，如果\(R<2L/T_{s}\)，则变换器在所有占空比下都会工作在CCM。

这个结果可以应用于并非纯线性电阻的负载。有效电阻负载可以定义为直流输出电压与直流负载电流的比值\(R=V/I\)。该有效电阻可用于上述等式。

其他变换器也可以进行类似的工作模式边界分析。Boost变换器在第5.3节中进行了分析，Buck-Boost作为第一个家庭作业。表5.1列出了三种基本DC-DC变换器的分析结果。在每种情况下，无量纲参数\(K\)定义为\(K=2L/(RT_{s})\)，并且模式边界如下所示：

\[K>K_{crit}(D)-or-R<R_{crit}(D)--CCM\\K<K_{crit}(D)-or-R>R_{crit}(D)--DCM \tag{5.8}
\]

Tab 5.1 CCM-DCM mode boundaries for the buck, boost, and buck-boost converters.