poj1654 -- Area (任意多边形面积)

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 20444		Accepted: 5567

Description

You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2. 

For example, this is a legal polygon to be computed and its area is 2.5: 

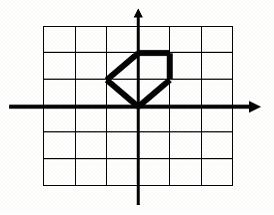
Input

The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.

Output

For each polygon, print its area on a single line.

Sample Input

4
5
825
6725
6244865

Sample Output

0
0
0.5
2

题意：

从坐标(0, 0)开始，向 8 个方向画线段，线段的起终点均为整点，问围成的多边形面积。

总结：

将多面形面分成若干个三角形面积和，用向量求任意多边形的有向面积（包括非凸多边形）。设一三角形三点坐标：A(x1, y1), B(x2, y2), C(x3, y3)，则面积的行列式形式如下：

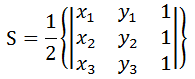
按第三列展开：

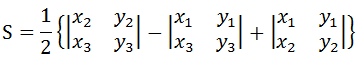
这样求出一个三角形的有向面积，顺时针为负，逆时针为正。

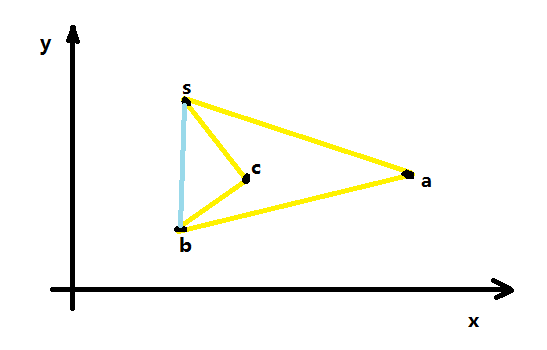
如上图黄色线段围成的非凸多边形也可用此方法求面积，用此方法其面积表示为：

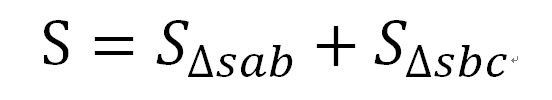
其中两个三角形的有向面积符号相反，即可求出此多边形真实面积（求出的有向面积要取绝对值）。

结论：

任意多变形的面积公式，其中(x1, y1), (x2, y2), (x3, y3) ... (xn, yn)为多边形的顶点，按顺（逆）时针排列：

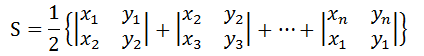
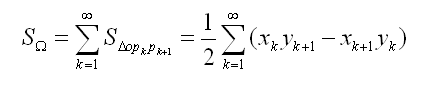
此题代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int dx[10] = { 0,-1,0,1,-1,0,1,-1,0,1 };
int dy[10] = { 0,-1,-1,-1,0,0,0,1,1,1 };
string str;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin>>t;
    while(t--)
    {
        cin>>str;
        long long ans=0, px=0, py=0, nx=0, ny=0;
        int len=str.size(); //.size()是无符号整型,有坑
        for(int i=0; i<len-1; i++)
        {
            int t0=str[i]-'0';
            px=nx+dx[t0];
            py=ny+dy[t0];
            ans+=(nx*py - ny*px);//向量求多边形有向面积,这里直接求两倍面积
            nx=px;
            ny=py;
        }
        if(ans<0)ans=-ans;
        cout<<ans/2;
        if(ans%2) cout<<".5";
        cout<<endl;
    }
    return 0;
}