仿射密码-fanfie--affine

仿射密码

仿射密码 是一种专情密码，一对一替换 ~~

加密函数是 e(x) = ax + b (mod m) 其中a和m 互质，m是字母的数目。

解码函数是 d(x) = a^-1(x - b) (mod m) (打不出来凑合一下 a^-1 乘法逆元)

仿射例题

【攻防世界】 - - fanfie

先上题，该题来源于 BITSCTF 。【题目链接】

下载附件，得到如下的字符串。长度不长，大写字母和数字组成。很容易让人想到 Base64/32 解密。

MZYVMIWLGBL7CIJOGJQVOA3IN5BLYC3NHI

先简单提一下详细介绍可以看一下网上大佬的这篇关于base系列的加密解密

Base64 ：由 0-9、a-z、A-Z、+、/ 及后缀 “=” 组成将任意字节序列数据编码成ASCII字符串

Base32 ：用32个可打印字符 A-Z、2-7 对任意字节数据进行编码

然而通过Base64解码并没有发现什么。（这题脑洞是真的大！！怪不得叫“ fanfie”-幻想）

通过百度大佬题解才知：

[ ] 将BITSCTF 进行Base32加密附 Base32加密网站
```
IJEVIU2DKRDA====
```
[ ] 得到的这串密文与题目给出的字符串进行比对
```
MZYVMIWLGBL7CIJOGJQVOA3IN5BLYC3NHI

IJEVIU2DKRDA====
```

发现上面相同的字母对应的下面的字母也一致。（如 M - I 、L - D）既然如此，那便有迹可循。

因为是Base32编码。那么对A-Z、2-7 进行编码:

A	B	C	D	E	F	G	H
0	1	2	3	4	5	6	7
I	J	K	L	M	N	O	P
8	9	10	11	12	13	14	15
Q	R	S	T	U	V	W	X
16	17	18	19	20	21	22	23
Y	Z	2	3	4	5	6	7
24	25	26	27	28	29	30	31

由此更直观可见，字母对应关系

3 ->11 4 ->24 8 ->12 20 ->8 21->21 25->9 26->22

这种一个字母替换一个字母的替换密码就是 仿射密码

加密函数是 e(x) = ax + b (mod m) 其中a和m 互质，m是字母的数目。

解码函数是 d(x) = a^-1(x - b) (mod m) (打不出来凑合一下 a^-1 乘法逆元)

如何进行仿射解密呢？我们有俩种方法：

进行肉眼勘测和手动计算
python脚本自动跑

先来看第一种：由上述所有条件，我们可以自豪的断定：仿射密码的 a = 13 b = 4

经过仿射解密可得：

MZYVMIWLGBL7CIJOGJQVOA3IN5BLYC3NHI --> IJEVIU2DKRDHWUZSKZ4VSMTUN5RDEWTNPU

第二种，上脚本：借鉴大佬仿射加密解密脚本欧几里得算法求解乘法逆元

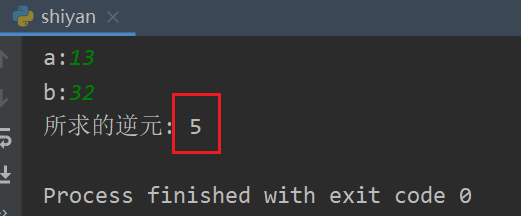
已知加密仿射的 a：13 b：4 模：32 第一步先求解 13关于模32的逆元

# 欧几里德算法求最大公约数

def get_gcd(a, b):

    k = a // b

    remainder = a % b

    while remainder != 0:

        a = b

        b = remainder

        k = a // b

        remainder = a % b

    return b

# 改进欧几里得算法求线性方程的x与y

def get_(a, b):

    if b == 0:

        return 1, 0

    else:

        k = a // b

        remainder = a % b

        x1, y1 = get_(b, remainder)

        x, y = y1, x1 - k * y1

    return x, y

a = input('a:')

b = input('b:')

a, b = int(a), int(b)

# 将初始b的绝对值进行保存

if b < 0:

    m = abs(b)

else:

    m = b

flag = get_gcd(a, b)

# 判断最大公约数是否为1，若不是则没有逆元

if flag == 1:

    x, y = get_(a, b)

    x0 = x % m  # 对于Python '%'就是求模运算，因此不需要'+m'

    print("所求的逆元:", x0)  # x0就是所求的逆元

else:

    print("Do not have!")

k1:仿射加密函数中的a

k2:仿射加密函数中的b

k3:13关于模32 的逆元

输入到下面java代码中

import java.util.Scanner;

public class Main{

    public static void main(String[] args) {

        char[] form = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N',

                'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', '2', '3', '4', '5', '6', '7'};

        Scanner sc = new Scanner(System.in);

        System.out.println("请输入待加密的明文：");

        String MingWen = sc.nextLine();

        MingWen=MingWen.toUpperCase();

        final int K1 = 13;  //仿射加密函数中的a

        final int K2 = 4;  //仿射加密函数中的b

        final int K3 = 5;  // 13关于 模32 的逆元

        int [] cipherNum=new int[MingWen.length()];//用来存储数字化的密文

        encryption(MingWen,form,K1,K2,K3,cipherNum);

    }

    public static void encryption(String MingWen,char[] form,int K1,int K2,int k3,int[] cipherNum){

        char[] pla=new char[MingWen.length()];

        for (int i = 0; i <MingWen.length() ; i++) {

            pla[i]=MingWen.charAt(i);

        }

        int[] MingWenNumber=new int[pla.length];

        for (int i = 0; i <pla.length ; i++) {

            for (int j = 0; j <form.length ; j++) {

                if (form[j]==pla[i]) {

                    MingWenNumber[i] = j;

                }

            }

        }

        //通过脚标将明文全部转化为数字

        char[] cipher = new char[MingWen.length()];

        char[] JieMI = new char[MingWen.length()];

        int len = MingWen.length();//cipher密码数组 用来存储密文

        for (int i = 0; i <MingWen.length() ; i++) {

            int a= Math.floorMod((K1*MingWenNumber[i]+K2),32);

            cipherNum[i]=a;

            cipher[i]=form[a];

            //计算密文并存入数组中

        }

        System.out.println("加密结果是：");

        System.out.println(cipher);

        for (int i =0;i<len;i++){

            JieMI[i]=form[Math.floorMod(k3*(MingWenNumber[i]-K2),32)];

        }

        System.out.println("解密结果是：");

        System.out.println(JieMI);

    }

}

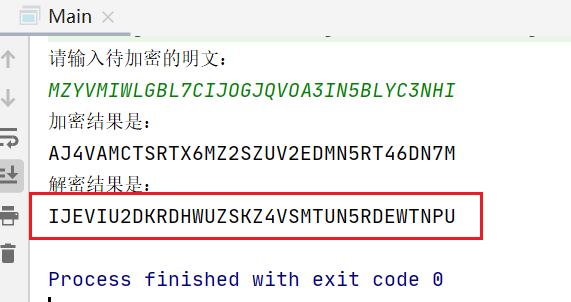
IJEVIU2DKRDHWUZSKZ4VSMTUN5RDEWTNPU

最后一步啦~ 对脚本跑出的代码进行 Base32 解码。网站同上。

BITSCTF{S2VyY2tob2Zm}

再来一简单题！

【bugkuCtf】 -- affine

题目链接请戳这里

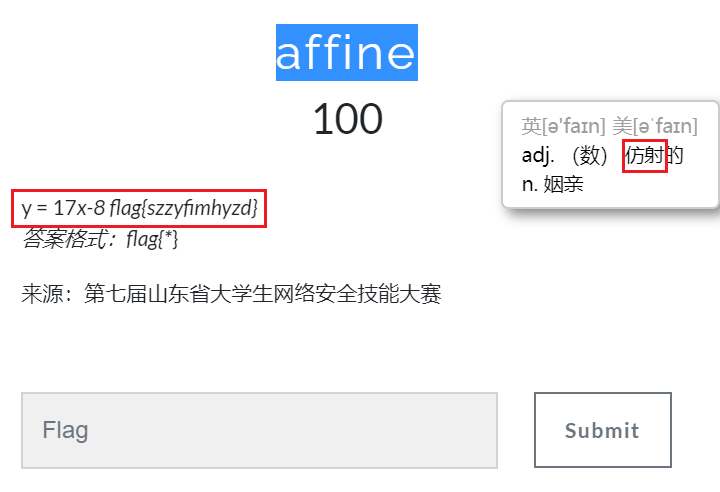
u1s1，该题目就非常实诚。直接给出 a / b 以及密文并且 affine 直接明示这是仿射解密。

E(x) = (ax + b) (mod m) a=17 b = -8

szzyfimhyzd

话不多说，我们可以继续使用上面的脚本也可以使用下面一种更快的脚本搬自这位大佬

def get(a, b):

    if b == 0:

        return 1, 0

    else:

        k = a //b

        remainder = a % b

        x1, y1 = get(b, remainder)

        x, y =y1, x1 - k * y1

    return x, y

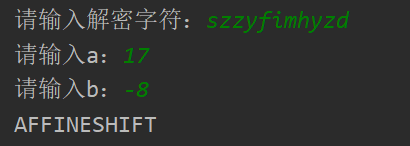
s = input("请输入解密字符：").upper()

a = int(input("请输入a："))

b = int(input("请输入b："))

#求a关于26的乘法逆元

x, y = get(a, 26)

a1 = x % 26

l= len(s)

for i in range(l):

    cipher = a1 * (ord(s[i])- 65 - b) % 26

    res=chr(cipher + 65)

    print(res, end='')

因为题目已经明确给出，所以直接进行解析就好。

preflag = "szzyfimhyzd"

flags = []

for i in preflag:

    flags.append(ord(i)-97)

flag = ""

for i in flags:

    for j in range(0,26):

        a = (17 * j - 8) % 26

        if(a == i):

            flag += chr(j+97)

print(flag)

那最后的flag就是：

affineshift

结语

最后：其实我蛮惊奇的。 fanfie && affine 取名上十分巧妙。

( 前一题是不是有暗示的意味在呢~~手动狗头）

宝藏软件推荐

【强烈安利】无意间知道了这个神仙软件 captfencoder (点击下载哦~)

里面聚合编码转换古典密码密码学其他编码实用工具！！

还是老规矩：关于以上链接引用【侵权删】

若有错误之处，还请多多指正~~

【转载请放链接】 https://www.cnblogs.com/Jlay/p/crypto_fangshe.html