基于python的数学建模---图论模型（Floyd）

import numpy as np

inf = 99999  # 不连通值
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
             [1, 0, 5, inf, 2, inf, inf, inf, inf],
             [inf, inf, 0, 1, inf, 6, inf, inf, inf],
             [inf, inf, inf, 0, inf, 7, inf, 9, inf],
             [inf, 2, 3, inf, 0, 4, 2, inf, 8],
             [inf, inf, 6, 7, inf, 0, inf, 2, inf],
             [inf, inf, inf, inf, inf, 1, 0, inf, 3],
             [inf, inf, inf, inf, inf, inf, 1, 0, 2],
             [inf, inf, inf, inf, 8, inf, inf, 2, 0]]

def Floyd(graph):
    N = len(graph)
    A = np.array(graph)
    path = np.zeros((N, N))
    for i in range(0, N):
        for j in range(0, N):
            if A[i][j] != inf:
                path[i][j] = j
    for k in range(0, N):
        for i in range(0, N):
            for j in range(0, N):
                if A[i][k] + A[k][j] < A[i][j]:
                    A[i][j] = A[i][k] + A[k][j]
                    path[i][j] = path[i][k]
    for i in range(0, N):
        for j in range(0, N):
            path[i][j] = path[i][j] + 1
    print('距离 = ')
    print(A)
    print('路径 = ')
    print(path)

Floyd(mtx_graph)

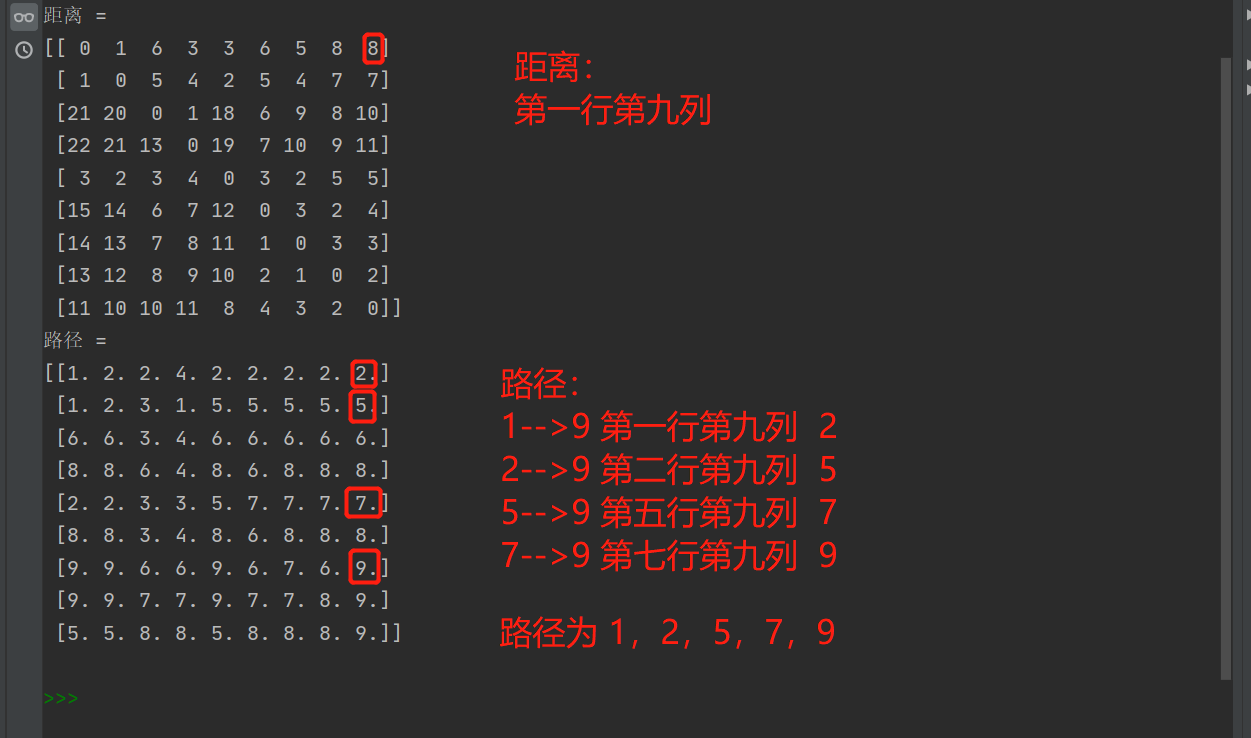
距离 =
[[ 0 1 6 3 3 6 5 8 8]
[ 1 0 5 4 2 5 4 7 7]
[21 20 0 1 18 6 9 8 10]
[22 21 13 0 19 7 10 9 11]
[ 3 2 3 4 0 3 2 5 5]
[15 14 6 7 12 0 3 2 4]
[14 13 7 8 11 1 0 3 3]
[13 12 8 9 10 2 1 0 2]
[11 10 10 11 8 4 3 2 0]]
路径 =
[[1. 2. 2. 4. 2. 2. 2. 2. 2.]
[1. 2. 3. 1. 5. 5. 5. 5. 5.]
[6. 6. 3. 4. 6. 6. 6. 6. 6.]
[8. 8. 6. 4. 8. 6. 8. 8. 8.]
[2. 2. 3. 3. 5. 7. 7. 7. 7.]
[8. 8. 3. 4. 8. 6. 8. 8. 8.]
[9. 9. 6. 6. 9. 6. 7. 6. 9.]
[9. 9. 7. 7. 9. 7. 7. 8. 9.]
[5. 5. 8. 8. 5. 8. 8. 8. 9.]