微积分 I 笔记

1.1 集合

这一节复习了高中关于集合的基础知识

介绍了一些新的概念

• 笛卡尔积 (Cartesian Product)
  
  集合 \(X\) 与 \(Y\) 的笛卡尔积 (直积) \(X \times Y\) 是指包含了所有第一个成员属于 \(X\)，第二个成员属于 \(Y\) 的所有有序对的集合
  
  \(A\times B=\{(x, y)|x \in A, y \in B\}\)

• 邻域 (neignbourhood)
  
  点 \(a\) 的 \(\delta\) \((\delta>0)\)邻域：
  
  指开区间 \((a-\delta, a+\delta)\)，也即 \(U(a, \delta)=\{x| |x-a|<\delta\}\)

• 去心邻域
  
  点 \(a\) 的 \(\delta (\delta>0)\) 的去心邻域 (即不包括点 \(a\))：
  
  \(U^0 (a, \delta)=\{x| 0<|x-a|<\delta\}\) (去心标记方式是 \(U\) 上写一个小 \(0\))

1.2 函数

1.3 数列极限 I

1. 引入
   
   对于无限数列 \(a_n=\frac{n}{n+1}\)，\(a_n \rightarrow 1\) (趋近于 \(1\))
   
   关于 \(0.9999... = 1\)

2. 数列极限的定义
   
   对于 \(\{x_n\}\)，若 \(\exist a\)，\(\forall \epsilon > 0\)，都 \(\exist N\)，使得对于所有 \(n>N\) 的 \(x_n\) 都满足 \(|x_n-a|<\epsilon\)
   
   那么我们就称 \(a\) 为 \(\{x_n\}\) 的极限 (或 \(\{x_n\}\) 收敛于 \(a\))，也即 \(\lim \limits_{n\to +\infty} x_n=a\)
   
   这个定义的几何理解：对于以极限 \(a\) 为中心，以任意常数 \(\epsilon\) 为半径的邻域，一定能够找到数列中的某一项 \(a_N\)，使得这一项之后的所有项的取值全部落在该邻域内

3. 证明数列的极限 (即找到存在的 \(N\))
   
   

1.4 数列极限 II

1. 若 \(\{x_n\}\) 收敛，则其极限唯一
2. 若 \(\{x_n\}\) 收敛，其有界
   • 有界是收敛的必要条件 (即收敛必有界，有界不一定收敛，例 \(\{1, -1, 1, -1, 1...\}\))
   • 若数列单调有界，则必收敛
3. \(\lim \limits_{n\to \infty} x_n=a (a>0), \exist N, n > N, x_n > 0\)
4. 子数列：与子集的区别：子数列中项的相对顺序与原数列一致
   • 若某数列收敛于 \(a\)，则其子数列也收敛于 \(a\)
   • 若找到某个子数列不收敛，则原数列一定发散
   • 若找到两个子数列收敛，但其极限不同，则原数列不收敛 \(e.g. \{1, -1, 1, -1, 1, ...\}\)
   • 原数列收敛的充要条件：其奇数项子数列与偶数项子数列均收敛，且极限相同

1.5 函数极限 I

1. 函数极限 (趋近正无穷)
   
   当 \(x\to + \infty\) 时，若 \(\exist a, \forall \epsilon, \exist X\)，使得 \(x>X\) 时，\(|f(x)-a|<\epsilon\)
   
   则我们称函数趋近正无穷时极限为 \(a\)，即 \(\lim \limits_{x\to+\infty} f(x)=a\)

2. 函数极限 (趋近负无穷)

3. 函数极限 (趋近无穷(正&&负))
   
   当 \(x\to \infty\) 时，若 \(\exist a, \forall \epsilon, \exist X (X>0)\), 使得 \(|x|>X\) 时，\(|f(x)-a|<\epsilon\)
   
   则 \(\lim \limits_{x\to\infty}f(x)=a\)

4. 函数极限 (趋近某个有限值 \(x_0\))
   
   当 \(x\to x_0\) 时，若 \(\exist a, \forall \epsilon, \exist \delta > 0\)，使得 \(0<|x-x_0|<\delta\) 时，\(|f(x)-a|<\epsilon\)
   
   则 \(\lim \limits_{x\to x_0}=a\)
   
   注意：由于 \(x\) 是趋近 \(x_0\)，所以在讨论时 \(x\) 是取不到 \(x_0\) 的。因此，\(f(x)\) 在 \(x_0\) 处可以没有定义，只需要在 \(x_0\) 的去心邻域内有定义即可

5. 左极限与有极限

   • 左极限 (即趋近点 \(x_0\) 的左侧的极限，\(x<x_0\))：以 \(x \to x^{-}_0\) 表示
   • 右极限 (即趋近点 \(x_0\) 的右侧的极限，\(x>x_0\))：以 \(x \to x^{+}_0\) 表示
   • 左右极限定理：\(\lim \limits_{x\to x_0}f(x)=a \iff \lim \limits_{x \to x^{-}_0}f(x)=\lim \limits_{x \to x^{+}_0}f(x)=a\)
   • 推论1：若左(右)极限不存在，则 \(x\to x_0\) 极限不存在
   • 推论2：若左右极限均存在但极限不相等，则 \(x\to x_0\) 极限不存在

6. 函数极限的几何理解：
   
   以极限 \(a\) 为中心，任意 \(\epsilon\) 为半径的邻域一定能够 "框住" 由某处 \(x=X\) 开始到无穷 (正或负) 的所有函数图像
   
   若讨论函数趋近某个定值 \(x_0\) 的极限时，则是以极限 \(a\) 为中心，任意 \(\epsilon\) 为半径的邻域一定能够 "框住" 某个以 \(x_0\) 为中心的去心邻域范围所对应的函数图像

1.5 函数极限 II

1. 唯一性：若极限存在，则在该点的极限是唯一的
2. 局部有限性：若趋近于 \(x_0\) 的极限存在，则一定存在 \(x_0\) 的去心邻域，函数在该范围内有界
3. 局部保号性：若 \(\lim \limits_{x \to x_0} f(x)=a (a>0)\)，则一定存在 \(x_0\) 的去心邻域，函数在该范围内大于 \(0\)
4. 取函数 \(f(x)\) 的一系列值形成数列 \(\{x_n\}\): 若 \(\lim \limits_{x\to x_0}f(x)=a\)，则 \(\lim \limits_{x\to x_0}\{x_n\}=a\)
   • 推论1：若 \(\exist \{x_n\}\) 极限不存在，则原函数极限不存在
   • 推论2：若 \(\exist \{x_n\}, \{y_n\}\) 极限存在但不相等，则原函数极限不存在
5. \(f(x)=a+\alpha(x), \lim \limits_{x\to x_0} \alpha(x)=0\)，则 \(\lim \limits_{x\to x_0} f(x)=a\)

1.6 无穷小与无穷大

1. 无穷小
   
   无限趋近于 \(0\)
   
   \(\lim \limits_{x\to x_0} f(x)=0\) 此时 \(f(x)\) 即是 \(x\to x_0\) 的无穷小

   • 无穷小 \(+/-/\times\) 无穷小仍是无穷小
   • 无穷小 \(\times\) 有界仍是无穷小
   • 无穷小 \(\div\) 无穷小可能是：常数，无穷大 (\(\infty\))，无穷小 (\(0\))

2. 无穷大
   
   即 \(+\infty\) 与 \(-\infty\)

   • 无穷大 \(\times\) 无穷大仍是无穷大 (注意符号判断)
   • 无穷大 \(+\) 有界仍是无穷大
   • 无穷大 \(+/-\) 无穷大可能是：常数，无穷大 (\(\infty\))，无穷小 (\(0\))

1.7 极限的运算法则

1. 四则运算
   
   若 \(\lim f(x)=a, \lim g(x)=b\) (对所有的变化过程都成立)

   • \(\lim (f(x)\pm g(x))=\lim f(x)\pm \lim g(x)\)
   • \(\lim (f(x)g(x))=\lim f(x)\times \lim g(x)\)
   • \(\lim \frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}(b\neq 0)\)

2. 常数和与 \(x\) 无关的变量 可以提出极限外

   • \(\lim c\cdot f(x)=c \lim f(x)\)
   • \(\lim yf(x)=y\lim f(x)\) (\(y\) 与 \(x\) 无关)
   • 幂：\(\lim f(x)^n=(\lim f(x))^n\)

3. 分配律：两个条件：是有限个函数且每个函数存在极限
   
   \(\lim (f_1(x)+f_2(x)+...+f_N(x))=\lim f_1(x)+\lim f_2(x)+...+\lim f_N(x)\)，\(N\) 为有限的

4. 复合函数求极限
   
   对于复合函数 \(u=\phi (x), y = f(u)\)
   
   \(\lim \limits_{x\to x_0} f[\phi (x)]=f[\lim \limits_{x\to x_0} \phi(x)]\)

5. \(\lim u(x)^{v(x)}\)
   
   \(\lim u(x)=a, \lim v(x)=b\) 则 \(\lim u(x)^{v(x)}=a^b\)
   
   证：\(\lim u(x)^{v(x)}=\lim e^{\ln u(x)^{v(x)}}=\lim e^{v(x) \ln u(x)}\)
   
   根据复合函数求极限法则
   
   \(\lim e^{v(x) \ln u(x)}=e^{\lim v(x) \ln u(x)}=e^{\lim v(x) \ln (\lim u(x))}=e^{b\ln a}=e^{\ln a^b}=a^b\)

6. 求函数极限的相关题目
   
   \(\lim \limits_{x\to a}=...\)，\(...\) 为：

   • 多项式或普通的有理分式：直接将 \(x=a\) 代入，极限可能是常数，\(0\) 或 \(\infty\)
   • 代入后 \(\frac{\infty}{\infty}\) 型：
     
     若分子分母次数相同：极限为 最高次的系数之比
     
     若分母次数大于分子次数：极限为 \(0\)
     
     若分子次数大于分母次数：极限为 \(\infty\)
   • 代入后 \(\frac{0}{0}\) 型：
     
     分子/分母有理化、洛必达法则：极限可能是常数，\(0\) 或 \(infty\)
   • 无限项之和
     
     例：求 \(\lim \limits_{n\to \infty}(\frac{1}{n^2}+\frac{2}{n^2}+...+\frac{n}{n^2})\) 的极限
     
     注意：这里 \(n\to \infty\) ，所以后面的项是无限的，不能使用分配律将极限拆开
     
     所以 \(\lim \limits_{n\to \infty}(\frac{1}{n^2}+\frac{2}{n^2}+...+\frac{n}{n^2}) =\lim \limits_{n\to \infty} \frac{ \frac{1}{2} n(n+1)}{n^2}=\frac{1}{2}\)

1.8.1 极限的存在准则

1. 夹逼定理
   
   对于函数 \(f(x), g(x), h(x)\)
   
   满足对于 \(U(x_0, r)\) (\(x_0\) 的半径为 \(r\) 的去心邻域)，\(g(x)\leq f(x) \leq h(x)\)
   
   若 \(\lim \limits_{x\to x_0} g(x)=h(x)=a\)，则 \(\lim \limits_{x\to x_0} f(x)=a\)

   • 例：求 \(\lim \limits_{n\to \infty} \frac{2^n}{n!}\)
     
     \(0<\frac{2^n}{n!}=\frac{2}{1} \times \frac{2\times 2\times ..2}{2\times 3 \times... (n-1)} \times \frac{2}{n}<\frac{4}{n}\) (小小的放缩)
     
     又 \(\lim \limits_{n\to \infty} 0 = \lim \limits_{n\to \infty} \frac{4}{n}=0\)
     
     根据夹逼定理 \(\lim \limits_{n\to \infty} \frac{2^n}{n!}=0\)

2. 单调有界数列必有极限
   
   即：单调增有上界数列必有极限；单调减有下界数列必有极限 (一定会增/减到接近界，所以必有极限)

   • 例：\(a>0, x_1=\sqrt{a},x_n=\sqrt{a+x_{n-1}}\)
     
     \(\sqrt{a}<\sqrt{a+\sqrt{a}}\)，即 \(x_1<x_2\)
     
     对于 \(x_{n-1}<x_n\)
     
     \(a+x_{n-1}<a+x_n\)
     
     \(\sqrt{a+x_{n-1}}<\sqrt{a+x_n}\)
     
     \(x_n<x_{n+1}\)
     
     所以数列单调递增
     
     \(x_1=\sqrt{a}<\sqrt{a}+1\)
     
     对于 \(x_n<\sqrt{a}+1\)
     
     \(x_{n+1}=\sqrt{a+x_n}<\sqrt{a+\sqrt{a}+1}<\sqrt{a+2\sqrt{a}+1}=\sqrt{(\sqrt{a}+1)^2}=\sqrt{a}+1\)
     
     所以数列存在上界 \(\sqrt{a}+1\)
     
     综上述，数列存在极限。设 \(\lim \limits_{n\to \infty} \{x_n\}=b\)
     
     \(x_n=\sqrt{a+x_{n-1}}\)
     
     \(\lim \limits_{n\to \infty} \{x_n\}=\lim \limits_{n\to \infty} \sqrt{a+x_{n-1}}\)
     
     \(\lim \limits_{n\to \infty} \{x_n\}=\sqrt{\lim \limits_{n\to \infty} (a+x_{n-1})}\)
     
     \(b=\sqrt{a+b}\)
     
     解出该式即可求出极限 \(b\)

1.8.2 两个重要极限

1. \(\lim \limits_{x\to 0} \frac{\sin x}{x}=1\)
   
   高中知识：\(y= \sin x\) 与 \(y=x\) 在 \(x_0=0\) 处的导数相等
   
   推论：\(\lim \limits_{x\to 0} \frac{\sin \alpha x}{x}=\alpha\) (将 \(\alpha x\) 看成整体并配成原式)

2. \(e\) 的定义：\(\lim \limits_{n \to \infty} (1+\frac{1}{n})^n=e\)

   • 例：求 \(\lim \limits_{x\to +\infty}=(1-\frac{1}{x})^{\sqrt{x}}\)
     
     \(=\lim \limits_{x\to \infty} (1+\frac{1}{\sqrt{x}})^{\sqrt{x}} (1-\frac{1}{\sqrt{x}})^{\sqrt{x}}\)
     
     \(=\lim \limits_{x\to \infty}(1+\frac{1}{\sqrt{x}})^{\sqrt{x}}[(\lim \limits_{x\to \infty}(1+ \frac{1}{-\sqrt{x}}))^{-\sqrt{x}}]^{-1}\)
     
     \(=e\times \frac{1}{e}\)
     
     \(=1\)

1.9 无穷小的比较

1. \(\lim f(x)=0, \lim g(x)=0, g(x)\neq 0\)

   • \(\lim \frac{f(x)}{g(x)}=0\)，则 \(f(x)\) 是 \(g(x)\) 的高阶无穷小，记为 \(f(x)=o(g(x))\)
   • \(\lim \frac{f(x)}{g(x)}=\infty\)，则 \(f(x)\) 是 \(g(x)\) 的低阶无穷小
   • \(lim \frac{f(x)}{g(x)}=c (c\neq 0)\)，则 \(f(x)\) 是 \(g(x)\) 的同阶无穷小
     
     若 \(c=1\)，\(f(x)\) 是 \(g(x)\) 的等价无穷小，记为 \(f(x)\sim g(x)\)
     
     下面的 \(2\sim 6\) 将会给出 \(4\) 个常用的等价无穷小对，做题时可以进行替换简化计算

2. \(\ln (1+x) \sim x, x\to 0\)

3. \(e^x-1 \sim x, x\to 0\)
   
   推论：\(a^x-1 \sim x\ln a, x\to 0\)

4. \(\sqrt[n]{1+x}-1 \sim \frac{1}{n}x, x\to 0\)
   
   这个结论证明比较难，先引入一个式子(易知成立)：\(a^n-1=(a-1)(a^{n-1}+a^{n-2}+...+a+1)\)
   
   \(\therefore a-1=\frac{a^n-1}{(a-1)(a^{n-1}+a^{n-2}+...+a+1}\)
   
   直接将 \(\sqrt[n]{1+x}=(1+x)^{\frac{1}{n}}\) 看作 \(a\) 并代入上式
   
   \((1+x)^{\frac{1}{n}}-1=(1+x-1)((1+x)^{\frac{n-1}{n}}+(1+x)^{\frac{n-2}{n}}+...+(1+x)^{\frac{1}{n}}+1)\)
   
   \(\therefore \lim \limits_{x\to 0} \frac{x((1+x)^{\frac{n-1}{n}}+(1+x)^{\frac{n-2}{n}}+...+(1+x)^{\frac{1}{n}}+1)}{\frac{x}{n}}=n\lim \limits_{x\to 0} ((1+x)^{\frac{n-1}{n}}+(1+x)^{\frac{n-2}{n}}+...+(1+x)^{\frac{1}{n}}+1)n\times \frac{1}{n}=1\)
   
   注：\(n\) 一定是有穷的，\(n\) 若无穷极限的分配律不成立

5. \(\sin x \sim x, \tan x \sim x, x\to 0\)

6. 若 \(f_1(x) \sim f_2(x), g_1(x) \sim g_2(x)\) 且存在 \(\lim \frac{g_2(x)}{f_2(x)}\)，则 \(\lim \frac{g_1(x)}{f_1(x)}=\lim \frac{g_2(x)}{f_2(x)}\)

   • 只有两个无穷小之比才可以进行替换
   • 若分子或分母是若干个因子的乘积，可以仅对部分的因子进行无穷小替换

7. 例题 (均是 \(\frac{0}{0}\) 型)

   • \(\lim \limits_{x\to 0}\frac{\sin 2x}{x^3+3x}\)
     
     \(= \lim \limits_{x\to 0}\frac{2x}{x^3+3x}=\lim \limits_{x\to 0}\frac{2}{x^2+3}=\frac{2}{3}\) (利用了 \(\sin x \sim x, x\to 0\))
   • \(\lim \limits_{x\to 0}\frac{(e^x-1)\sin x}{1-\cos x}\)
     
     \(=\lim \limits_{x\to 0}\frac{x\times x}{2 \sin^2 \frac{x}{2}}\)
     
     \(=\lim \limits_{x\to 0}\frac{x\times x}{2 \times \frac{x^2}{4}}=2\)

1.10.1 函数的连续性 I

1. 增量(改变量)
   
   \(\Delta x\) (自变量增量)
   
   \(\Delta y= f(x_0+\Delta x)-f(x_0)\) (因变量增量)
   
   注：增量可以为负

2. 函数在 \(x=x_0\) 处连续的定义
   
   \(f(x)\) 在 \(x_0\) 的邻域内有定义 (注意是邻域而非去心邻域，这意味着 \(x=x_0\) 时不一定需要有定义)
   
   定义一：\(\lim \limits_{\Delta x \to 0}\Delta y=\lim \limits_{\Delta x \to 0} [f(x_0+\Delta x)-f(x_0)]=0\)
   
   定义二：\(\lim \limits_{x\to x_0}f(x)=f(x_0)\)
   
   这些定义均包含三个条件：

   • 在 \(x_0\) 处有定义
   • \(x\to x_0\) \(f(x)\) 有极限
   • 极限 \(=f(x_0)\)

3. 关于左连续与右连续
   
   若 \(x_0\) 的右侧/左侧没有定义，则取 \(x_0\) 的左邻域/右邻域

4. 在区间上连续
   
   区间 \([x_1, x_2]\)
   
   在区间内部 \((x_1, x_2)\)，连续
   
   在 \(x=x_1\) 时右连续
   
   在 \(x=x_2\) 时左连续

5. 关于间断点 (不连续)

   • 无穷间断
     
     不满足条件一：即在 \(x\to x_0\) 时无定义
     
     例，对于函数 \(y=\frac{1}{x}\)，\(x=0\) 即是其的无穷间断点
   • 震荡
     
     不满足条件二：即 \(x\to x_0\) 时 \(f(x)\) 无极限
   • 跳跃
     
     不满足条件三：即极限不等于 \(f(x_0)\)
   • 可去
     
     同样不满足条件三：即极限不等于 \(f(x_0)\)

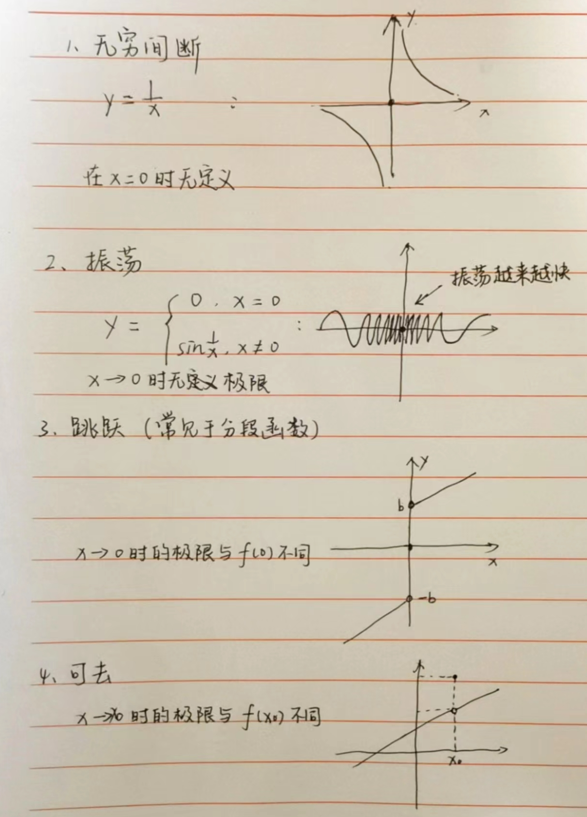
跳跃间断与可去间断属于第一类：当 \(x\to x_0\) 时左右极限均存在

而无穷间断与震荡间断属于第二类：左右极限不存在

1. 连续的几何解释：一笔画

1.10.2 函数的连续性 II

1. 函数运算对连续性的影响
   
   \(f(x), g(x)\) 均为连续函数
   
   四则运算：\(f(x) \pm g(x), f(x)\times g(x), \frac{f(x)}{g(x)} (g(x)\neq 0)\) 得出的新函数仍连续
   
   多项式：\(a_0x^n+a_1x^{n-1}+...+a_{n-1}x+a_n\) 一定在 \((-\infty, +\infty)\) 上连续
   
   复合函数：\(u=\phi (x), y=f(u)\) 均连续，复合函数 \(f(\phi (x))\) 也连续
   
   反函数：\(y=f(x)\) 连续并是单调函数，那么它的反函数也一定连续(注意，这里的单调条件是为了保证函数存在反函数)

2. 闭区间上连续的性质

   • 有界性：在 \([a, b]\) 上连续，函数值一定有界
   • 最值性：在 \([a, b]\) 上连续，函数一定有最大/最小值
   • 介值性：在 \([a, b]\) 上连续，函数的最大值为 \(M\)，最小值为 \(m\)，\(\forall c (m < c < M)\)，闭区间内一定存在 \(\epsilon\) 使得 \(f(\epsilon)=c\)
   • 零点存在定理：在 \([a, b]\) 上连续，若 \(f(a)f(b)<0\)，则在 \((a, b)\) 内一定存在至少一个零点 (即函数值为 \(0\) 的点)

2.1.1 导数的定义 I

1. 导数：用于描述函数的平均变化率(在 \(x=x_0\) 处切线的斜率)
   
   \(y=f(x)\) 在 \(U(x_0)\) 有意义
   
   \(x_0 \to x_0 + \Delta x, f(x_0) \to f(x+x_0)\)，则函数在 \(x=x_0\) 处的导数为 \(\lim \limits_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\)

2. 其他表述
   
   \(\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}\)
   
   \(\lim \limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\)

3. 利用导数的定义解题
   
   例：\(y=x^2\) 求 \(y'|_{x=2}\)
   
   \(x\to x+\Delta x, f(x) \to f(x+\Delta x)\)
   
   \(\Delta y = f(x+\Delta x)-f(x)=2x\Delta x+(\Delta x)^2\)
   
   \(y'|_{x=2}=\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim \limits_{\Delta x \to 0}(2x+\Delta x)=2x=4\)

4. 常见函数的导函数
   
   \(y=c, y'=0\)
   
   \(y=x^n, y'=nx^{n-1}\) (\(n\) 为整数)
   
   \(y=x^a, y'=ax^{a-1}\)
   
   \(y=\sin x, y'=\cos x\)
   
   \(y=\cos x, y'=-\sin x\)
   
   \(y= \ln x, y'=\frac{1}{x}\)
   
   \(y=\log_a x, y'=\frac{1}{x \ln a}\)
   
   \(y=a^x, y'=a^x\ln a\)
   
   \(y=e^x, y'=e^x\)

2.1.2 导数的定义 II

1. 导数的意义 \(\lim \limits_{x\to x_0}\frac{\Delta y}{\Delta x}\)

   • \(y=f(t)\) 时间-路程函数，\(f'(t)\) 表示瞬时速度
   • 在 \(x=x_0\) 处切线的斜率
   • 切线方程：\(y-y_0=f'(x_0)(x-x_0)\)
     
     法线方程：\(y-y_0=\frac{1}{f'(x_0)}(x-x_0)\)

2. 关于单侧导数
   
   在有定义的区间 \([a, b]\) 上
   
   在 \(x=a\) 时右可导，其右导数记为 \(f_{+}'(a)\)
   
   在 \(x=b\) 时左可导，其左导数记为 \(f_{-}'(b)\)
   
   在区间内部函数可导，其充要条件为 左右导数均存在且相等 (该结论一般用于证明某点是否可导)
   
   
   
   例：对于 \(y=|x|\)，讨论在 \(x=0\) 时是否可导
   
   \(f_{+}(0)=\lim \limits_{\Delta x \to o^{+}} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim \limits_{\Delta x \to 0^{+}} \frac{\Delta x}{\Delta x}=1\)
   
   \(f_{-}(0)=\lim \limits_{\Delta x \to o^{-}} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim \limits_{\Delta x \to 0^{-}} \frac{-\Delta x}{\Delta x}=-1\)
   
   \(\therefore f_{+}(0) \neq f_{-}(0)\)
   
   在 \(x=0\) 处函数不可导

3. 可导与连续的关系
   
   可导的几何意义：函数图像是光滑的
   
   连续的几何意义：函数图像可一笔画
   
   光滑的图像必能被一笔画，而可一笔画的图像不一定光滑(\(y=|x|\)) \(\iff\) 可导一定连续，连续不一定可导
   
   
   
   证明：
   
   可导意味着 \(\lim \limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x}\) 存在
   
   连续意味着 \(\lim \limits_{\Delta x \to 0} \Delta y=0\)
   
   可导必连续：\(\lim \limits_{\Delta x \to 0} \Delta y=\lim \limits_{\Delta x\to 0} (\frac{\Delta y}{\Delta x} \Delta x)=\lim \limits_{\Delta x\to 0} \frac{\Delta y}{\Delta x} \lim \limits_{\Delta x\to 0} \Delta x=0\)

2.2 求导法则

• \((u(x)+v(x))'=u'(x)+v'(x)\)
  
  \((u_1(x)+u_2(x)+...+u_n(x))'=u_1'(x)+u_2'(x)+...+u_n'(x)\)

• \((u(x)v(x))'=u'(x)v(x)+u(x)v'(x)\)
  
  \((cu(x))'=cu'(x)\)
  
  \((u(x)v(x)w(x))'=u'(x)v(x)w(x)+u(x)v'(x)w(x)+u(x)v(x)w'(x)\)

• \((\frac{u(x)}{v(x)})'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}\)

• 反函数的导数互为倒数
  
  \(y=f(x), x=\phi (y)\) 那么 \(f'(x)=\frac{1}{\phi '(y)}\)
  
  例：求 \(y=a^x\) 的导数
  
  \(x=log_a y (y>0)\)
  
  则 \((a^x)'=\frac{1}{(log_a y)'}=y \ln a=a^x \ln a\)

• 复合函数求导链式法则
  
  \(y=f(u), u=\phi(x)\)
  
  \(\frac{dy}{dx}=\frac{dy}{du} \cdot \frac{du}{dx}\)
  
  \((f(\phi(x)))'=f'(u) \cdot \phi '(x)\)
  
  例：求 \(f(x)=e^{sin^2 \frac{1}{x}}\) 的导数
  
  \(f'(x)=e^{sin^2 \frac{1}{x}} \cdot 2sin \frac{1}{x} \cdot cos \frac{1}{x} \cdot (-\frac{1}{x^2})\)

2.4 高阶导数

1. 二阶导数
   
   \(y''=\frac{d \frac{dy}{dx}}{dx}=\frac{d^2 y}{dx^2}\) (注意指数的位置)
   
   \(y'''\) (三阶导数)
   
   \(y^{(4)}\) (四阶导数)

2. 隐函数求导
   
   对于 \(x^2+y^2=r^2\)，求 \(\frac{d^2 y}{dx^2}\)
   
   两边同时对 \(x\) 求导：\(2x+2y \cdot \frac{dy}{dx}=0\) (第二项是复合函数求导)
   
   \(\frac{dy}{dx}=-\frac{x}{y}\) (再两边同时对 \(x\) 求导得到二阶导数)
   
   \(\frac{d^2 y}{dx^2}=-\frac{y-x\frac{dy}{dx}}{y^2}=-\frac{y+\frac{x^2}{y}}{y^2}=-\frac{y^2+x^2}{y^3}=-\frac{r^2}{y^3}\) (将 \(\frac{dy}{dx}=-\frac{x}{y}\) 代入)

3. 参数方程求导
   
   \(x=a(t-\sin t), y=a(1-\cos t)\)，求 \(\frac{d^2 y}{dx^2}\)
   
   \(\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{\sin t}{1-\cos t}\)
   
   \(\therefore \frac{d}{dx}(\frac{dy}{dx})=\frac{d}{dx}(\frac{\sin t}{1-\cos t})=\frac{d}{dt}(\frac{\sin t}{1-\cos t})\frac{1}{\frac{dx}{dt}}=-\frac{1}{a(\cos t-1)^2}\) (用到了反函数求导以及复合函数求导链式法则)
   
   讲一下自己对式子的理解：函数 \(f(t)\) 对 \(x\) 求导，而 \(t=\phi (x)\)，则 \(f(\phi (x))=f' \phi'\)，\(\phi'\) 通过 \(x=a(t-\sin t)\) 的反函数求导法则得出

4. 一些常见函数的高阶导数

   • \((u \pm v)^{(n)}=u^{(n)} \pm v^{(n)}\)
   • \((cu)^{(n)}=cu^{(n)}\)
   • \((uv)^{(n)}=\sum_{i=0}^n \C^i_n u^{((n-i))}v^{(i)}\)
   • \((\sin x)^{(n)}=\sin (x+\frac{n\pi}{2})\)
   • \((\cos x)^{(n)}=\cos (x+\frac{n\pi}{2})\)

2.5.1 微分I

• 微分(\(dy\))是函数改变量(\(\Delta y\))的线性主要部分
  
  \(f(x)\) 在 \(x_0\) 邻域内有定义，\(x_0+\Delta x\) 在邻域内
  
  若 \(\Delta y=f(x_0+\Delta x)-f(x_0)\) 可以表示为 \(\Delta y=A\Delta x+o(\Delta x)\) (\(A\) 是与 \(\Delta x\) 无关的常数，\(o(\Delta x)\) 是 \(\Delta x\) 的高阶无穷小)
  
  则我们称 \(f(x)\) 在 \(x_0\) 可微，其微分 \(dy=A \Delta x\)
  
  (\(\Delta y\) 是函数改变量的精确值，\(dy\) 是其的近似值)

• 一元函数在 \(x_0\) 可微 \(\iff\) 可导
  
  \(dy=f'(x_0)\Delta x=f'(x_0)dx\)
  
  这里是证明
  
  所以，定义中的常数 \(A\) 即是 \(f(x)\) 在 \(x_0\) 处的导数

• 微商(即导数)
  
  将 \(dy=f'(x)dx\) 式子转变一下即得到求导公式 \(f'(x)=\frac{dy}{dx}\)
  
  在一元函数内导数就是微分的分数形式

• 微分的几何意义
  
  

2.5.2 微分II

• 微分基本公式：\(dy=f'(x)dx\)

• 四则运算
  
  \(dc=c'dx=0\)
  
  \(d(u\pm v)=du \pm dv\)
  
  \(d(cu)=cdu\)
  
  \(d(uv)=vdu+udv\)
  
  \(d(\frac{u}{v})=(\frac{u}{v})dx=\frac{u'v-v'u}{v^2}dx=\frac{vdu-udv}{v^2}\)
  
  (对于分式求微分的相关题目，若分子次数大于等于分母，可以配成 \(x...+\frac{c}{x...}\) 的形式再求微分)

• 一阶微分的形式不变性
  
  对于 \(y=f(u)\)

  • 若 \(u\) 为自变量，\(dy=f'(u)du\)
  • 若 \(u\) 为函数 \(u=\phi (x)\)，则 \(dy=y'_xdx=f'(u)(\phi '(x)dx)=f'(u)du\)

• 隐函数求微分
  
  例：对于 \(x^2+2xy-y^2=2x\) 求 \(dy\)

  • 方法一：等式两边同时对 \(x\) 求导
    
    \(x+y+xy'-yy'=1\)
    
    \(\therefore y'=\frac{1-x-y}{x-y}, dy=y'dx=\frac{1-x-y}{x-y}dx\)
  • 方法二：等式两边同时求微分
    
    \(xdx+xdy+ydx-ydy=dx\)

• 微分的应用
  
  因为 \(\Delta y \approx dy=f'(x_0)dx\)
  
  所以 \(f(x_0+\Delta x)\) 可由 \(f(x_0)+f'(x_0)\Delta x\) 近似得出 (\(|\Delta x|\) 取很小)

• 等价无穷小的推出
  
  还记得上面的几个等价无穷小的结论(1.9-2)吗？它们可以由上式推导而来
  
  取 \(x_0=0, \Delta x=x\) 则有 \(f(x)\approx f(0)+f'(0)x\)
  
  这个式子同样可以用于近似计算 (当且仅当 \(x\) 很小的时候可以近似！)

3.1.1 微分中值定理

• 费马引理
  
  \(f(x)\) 在 \(x_0\), \(U(x_0)\) 处有定义且在 \(x_0\) 处可导
  
  若 \(f(x)\leq f(x_0)\) (或 \(f(x) \geq f(x_0)\)) 则 \(f'(x_0)=0\)
  
  非常符合直觉的结论，下面是证明 (\(f(x) \leq f(x_0)\)的情况)
  
  \(f_{-}'(x_0)=\lim \limits_{x\to 0^{-}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \geq 0\) (分子小于等于 \(0\), 分母小于 \(0\))
  
  \(f_{+}'(x_0)=\lim \limits_{x\to 0^{+}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \leq 0\) (分子小于等于 \(0\), 分母大于 \(0\))
  
  又 \(f(x)\) 在 \(x_0\) 处可导，所以 \(f_{-}(x_0)=f_{+}(x_0)=0\)

• 罗尔中值定理
  
  若 \(f(x)\) 满足：1. 在 \([a, b]\) 上连续 2. 在 \((a, b)\) 上可导 3. \(f(a)=f(b)\)
  
  则至少存在一个 \(\xi \in (a, b)\)，使得 \(f'(\xi)=0\)

• 拉格朗日中值定理
  
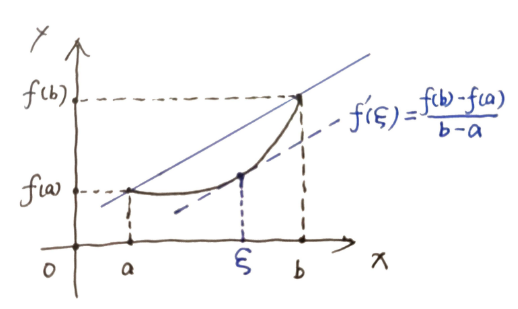
  若 \(f(x)\) 满足：1. 在 \([a, b]\) 上连续 2. 在 \((a, b)\) 上可导
  
  则至少存在一个 \(\xi \in (a, b)\) 使得 \(f'(\xi)=\frac{f(b)-f(a)}{b-a}\)
  
  罗尔中值定理是拉格朗日中值定理在 \(f(a)=f(b)\) 时成立的情况
  
  

3.1.2 柯西中值定理

若 \(f(x)\)和\(F(x)\) 满足：1. 在 \([a, b]\) 上连续 2. 在 \((a, b)\) 上可导 3. \(\forall x \in (a, b)\), \(F'(x) \neq 0\)

则至少有一点 \(\xi\) 使得 \(\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}\)

拉格朗日中值定理是柯西中值定理在 \(F(x)=x\) 时成立的情况

这里 用构造函数法+罗尔中值定理对柯西中值定理进行了证明

3.1.3 泰勒定理

• 介绍
  
  泰勒公式，是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件，泰勒公式可以用函数在某一点的\(n\)阶导数值做系数构建一个\(n\)次多项式来近似表达这个函数
  
  之前介绍的近似公式 \(f(x) \approx f(x_0)+f'(x_0)(x-x_0)\) 用某点的信息以 一次多项式 的形式描述附近函数的取值，误差可能较大

• 泰勒定理
  
  \(f(x)\) 可以表示成 \(x-x_0\) 的 \(n\) 次多项式加余项 \(R_n(x)\)
  
  \(f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x)\)
  
  拉格朗日型余项 \(R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{(n+1)}, \xi \in (x_0, x)\)
  
  拉格朗日余项实际是泰勒公式展开式与原式之间的一个误差值，如果其值为无穷小，则表明公式展开足够准确

• 麦克劳林公式
  
  泰勒公式在 \(x_0=0\) 时成立的情况，即
  
  \(f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+R_n(x)\)
  
  例：将函数 \(f(x)=e^x\) 使用麦克劳林公式展开 (\(f^{(n)}(0)=e^0=1\))
  
  \(e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+...+\frac{x^n}{n!}+\frac{e^{\theta x}}{(n+1)!}x^{n+1}\)，其中 \(f^{(n+1)}(\xi)=e^{\xi}=e^{\theta x}\)
  
  \(\therefore e^x \approx x+\frac{x^2}{2!}+...+\frac{x^n}{n!}\)
  
  
  
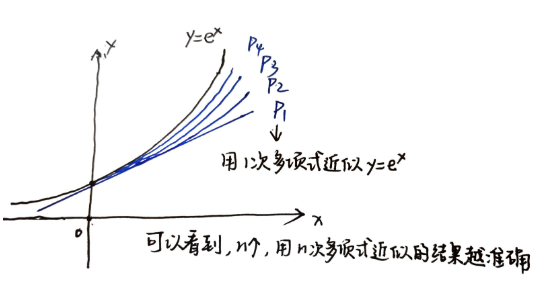
  另：类似的，\(\sin x \approx = x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-...+\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1}+R_{2m}\)

3.2 洛必达法则

1. 公式介绍
   
   若函数 \(f(x), g(x)\) 满足
   
   (1）\(\lim \limits_{x\to x_0}f(x)=\lim \limits_{x\to x_0}g(x)=0\) (\(\frac{0}{0}\) 型)
   
   (2) 在 \(x_0\) 的去心邻域内可导且 \(g'(x) \neq 0\)
   
   (3) \(\lim \limits_{x\to x_0}\frac{f'(x)}{g'(x)}=a\) (或者 \(\infty\))
   
   则 \(\lim \limits_{x\to x_0}\frac{f(x)}{g(x)}=\lim \limits_{x\to x_0}\frac{f'(x)}{g'(x)}=a\) (或者 \(\infty\))

2. 使用柯西中值定理进行证明
   
   首先可以发现，洛必达法则对 \(f(x)\) 与 \(g(x)\) 在 \(x_0\) 处的定义有无并不做要求
   
   不如令 \(f(x_0)=g(x_0)=0\) (这一步是为了满足应用柯西中值定理的条件)
   
   此时，\(f(x), g(x)\) 在 \(x_0\) 处定义，极限均存在且相等 (\(\lim \limits_{x\to x_0}f(x)=f(x_0)=0\))
   
   \(\because\) \(x\) 在 \(x_0\) 的去心邻域内，\(f(x), g(x)\) 在区间 \([x_0, x]\) 可导
   
   对 \(f(x), g(x)\) 应用柯西中值定理，则有
   
   \(\exist \xi \in (x_0, x)\) 使得 \(\frac{f(x)-f(x_0)}{g(x)-g(x_0)}=\frac{f(x)-0}{g(x)-0}=\frac{f(x)}{g(x)}=\frac{f'(\xi)}{g'(\xi)}\)
   
   \(\because \lim \limits_{x\to x_0}\frac{f(x)}{g(x)}=\lim \limits_{x\to x_0}\frac{f'(\xi)}{g'(\xi)}\)
   
   又 \(\xi in (x_0, x), x\to x_0\)，\(\because \xi \to x_0\) (可以将 \(x_0\) 理解为定值，\(x\) 在 \(x_0\) 的去心邻域内移动)
   
   最终有 \(\lim \limits_{x\to x_0}\frac{f(x)}{g(x)}=\lim \limits_{x\to x_0}\frac{f'(\xi)}{g'(\xi)}=\lim \limits_{\xi\to x_0}\frac{f'(\xi)}{g'(\xi)}=\lim \limits_{x\to x_0}\frac{f'(x)}{g'(x)}\)

3. 洛必达法则的适用范围
   
   不定式极限：
   
   \(\lim \frac{0}{0}\): 已证明，见上
   
   \(\lim \frac{\infty}{\infty}=\lim \frac{\frac{1}{\infty}}{\frac{1}{\infty}}=\lim \frac{0}{0}\)
   
   \(\lim 0\cdot \infty=\lim \frac{1}{\infty} \cdot \infty=\lim \frac{\infty}{\infty}\)
   
   \(\lim 0^0=\lim e^{\ln 0^0}=e^{\lim 0 \ln0}=e^{\lim 0\cdot \infty}\)
   
   \(\lim 1^{\infty}=\lim e^{\ln 1^{\infty}}=e^{\lim \infty \ln 1}=e^{\lim 0\cdot \infty}\)
   
   \(\lim \infty^{0}=\lim e^{\ln \infty^0}=e^{\lim 0\ln \infty}=e^{\lim 0 \cdot \infty}\)

4. 例题
   
   
   
   
   
   
   
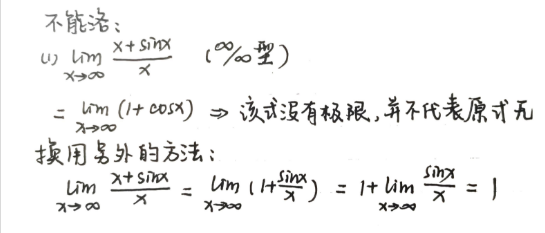
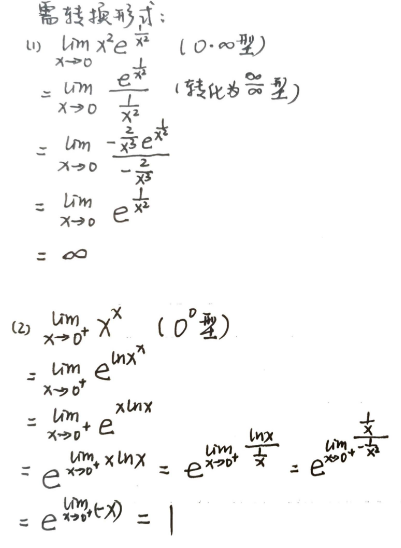
   运用洛必达法则解题时注意以下几点：

   • 要符合不定式条件 （如 \(\frac{0}{0}, \frac{\infty}{\infty}\)）
   • 结合重要极限，等价无穷小替换等方法简化计算
   • 若 \(\lim \frac{f'(x)}{g'(x)}\) 不存在也不等于 \(\infty\) 时，不能断言原式 \(\lim \frac{f(x)}{g(x)}\) 也不存在。应当采用洛必达以外的方法进行解题

3.3 函数单调性与凹凸性

1. 单调性
   
   单调递增 \(f'(x)>0\) 递减 \(f'(x)<0\) (若 \(f'(x)\geq 0\)，则等号只能在个别点成立)
   
   函数的分界点(函数单调性发生改变的点)：驻点 (\(f'(x)=0\) 的点)，导数不存在的点 (这是一个充分不必要条件)
   
   当解答关于分析函数单调性的相关题目时，研究函数的导数，先找到函数分界点，再对各个区间进行分段讨论
   
   
   
   例：分析函数 \(y=\sqrt[3]{x^2}\) 的单调性
   
   \(y'=\frac{2}{3}\frac{1}{\sqrt[3]{x}}\)
   
   \(x=0\) 是该函数的分界点，因为在此处导数不存在
   
   \(x<0\) 时，\(y'<0\)，函数单调递减；\(x>0\) 时，\(y'>0\)，函数单调递增

2. 凹凸性的定义
   
   (有没有联想到高中时接触过的极值点偏移类型的题目？)
   
   比较中点函数值与函数值中点的大小：对区间内任意 \(x_1<x_2\)，有
   
   凹：\(f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2}\)
   
   凸：\(f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2}\)

3. 凹凸性的性质
   
   凹：\(f''(x)>0\)
   
   凸：\(f''(x)<0\)
   
   这一性质通过观察函数图像切线斜率的变化可以很直观的理解；这里还是用拉格朗日中值定理进行证明
   
   
   
   对于定义域内的 \(x1, x2(x1<x2), x_0=\frac{x_1+x_2}{2}, f''(x)>0\) (证明 \(f''(x)>0\) 函数为凹函数)
   
   在 \([x_1, x_0]\)，\(f(x_0)-f(x_1)=f'(\xi_1)(x_0-x_1), \xi_1 \in (x_1, x_0)\)
   
   在 \([x_0, x_2]\)，\(f(x_2)-f(x_0)=f'(\xi_2)(x_2-x_0), \xi_2 \in (x_0, x_2)\)
   
   两式相减整理得
   
   \(2f(x_0)-[f(x_1)+f(x_2)]=\frac{1}{2} (x_2-x_1)(f'(\xi_1)-f'(\xi_2))\)
   
   对导函数 \(f'(x)\) 再次使用一次拉格朗日中值定理
   
   \(f'(\xi_1)-f'(\xi_2)=f''(\eta)(\xi_1-\xi_2), \eta \in (\xi_1, \xi_2)\)
   
   由条件可知 \(f''(\eta)>0, x_2-x_1>0, \xi_1-\xi_2<0\)
   
   \(\therefore 2f(x_0)-[f(x_1)+f(x_2)]=\frac{1}{2} (x_2-x_1)(f'(\xi_1)-f'(\xi_2))=\frac{1}{2} (x_2-x_1)f''(\eta)(\xi_1-\xi_2)<0\)
   
   \(\therefore f(x_0)<\frac{f(x_1)+f(x_2)}{2}\)
   
   x

4. 拐点
   
   类似研究单调性时的 分界点：函数的 拐点 是指 \(f''(x)=0\) 的点或者二阶导数不存在的点 (这是一个充分不必要条件)
   
   函数在经过拐点后，凹凸性发生改变 (这才是充要条件)
   
   当解答关于分析函数凹凸性的相关题目时，研究函数的二阶导数，先找到函数的拐点，再对各个区间进行分段讨论
   
   x

5. 利用函数的凹凸性进行证明
   
   例：求证 \(\frac{e^a+e^b}{2}>e^{\frac{a+b}{2}}, a\neq b\)
   
   对于 \(f(x)=e^x, f''(x)\=e^x>0\)
   
   \(\therefore f(x)\) 是凹函数，对于任意定义域内的 \(a, b\) 都有
   
   \(\frac{f(a)+f(b)}{2}>f(\frac{a+b}{2})\)
   
   得证

3.4.1 极值

1. 极大值(点)与极小值(点)
   
   \(U(x_0)\)，\(\forall x \in U(x_0^{\cap})\) 都有 \(f(x)<f(x_0)\)，那么称 \(f(x_0)\) 为一个极大值，\(x_0\) 为一个极大值点
   
   \(U(x_0)\)，\(\forall x \in U(x_0^{\cap})\) 都有 \(f(x)>f(x_0)\)，那么称 \(f(x_0)\) 为一个极小值，\(x_0\) 为一个极小值点
   
   极值是一个局部概念，对于某个函数，极值不唯一，也不一定相等

2. 极值点 \(\Rightarrow\) 驻点或导数不存在的点 (充分不必要)
   
   \(f(x)\) 在 \(x_0\) 可导，且在 \(x_0\) 取极值，则 \(f'(x_0)=0\) (可导函数的极值点一定是驻点)
   
   证：设在 \(x_0\) 取极大值，则 \(\forall x \in U(x_0^{\cap})\) 都有 \(f(x)<f(x_0)\)
   
   左导数 \(\lim \limits_{\Delta x \to 0^{-}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\geq 0\)
   
   右导数 \(\lim \limits_{\Delta x \to 0^{+}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\leq 0\)
   
   又函数在 \(x_0\) 可导 \(\therefore\) \(x_0\) 处左右导数相等，\(f'(x_0)=0\) 得证

3. 讨论定理 \(2\) 充要的补充条件
   
   \(f(x)\) 在 \((x_0-c, x_0+c)\) 内连续，在 \(x_0\) 的去心邻域上可导，且 \(f'(x_0)=0\) 或在 \(x=x_0\) 时导数不存在
   
   （1）左增右减：\(x\in(x_0-c, x_0), f'(x)>0; x\in(x_0, x_0+c), f'(x)<0\) 则 \(x_0\) 为极大值点
   
   （2）左减右增：则 \(x_0\) 为极大值点
   
   （3）左右均增(减)：\(f'(x)\) 在 \(x_0\) 处不变号，\(x_0\) 不是极值点
   
   
   
   运用该结论解答求极值点相关题目：
   
   (1) 在定义域内，找到驻点与导数不存在的点
   
   (2) 判断 \(f'(x)\) 在上述点左右的符号 (画 \(x-f'(x)-f\) 表, 3.4-32:00)

4. 若在 \(x=x_0\) 处有二阶导, \(f'(x_0)=0, f''(x_0)\neq 0\)：若 \(f''(x_0)>0\)，则 \(x_0\) 为极小值点；若 \(f''(x_0)<0\)，则 \(x_0\) 为极大值点
   
   证：当 \(f'(x_0)=0, f''(x_0)>0\)
   
   \(f''(x_0)=\lim \limits_{\Delta x\to 0}\frac{f'(x_0+\Delta x)-f'(x_0)}{\Delta x}=\lim \limits_{\Delta x\to 0}\frac{f'(x_0+\Delta x)}{\Delta x}>0\)
   
   \(\therefore \lim \limits_{\Delta x\to 0^{-}}f'(x_0+\Delta x)<0, \lim \limits_{\Delta x\to 0^{+}}f'(x_0+\Delta x)>0\)
   
   左减右增，\(\therefore x_0\) 为极大值点得证
   
   注意：当 \(f''(x_0)=0\) 时 \(x_0\) 可能为极值点，也可能不是，此时应采取结论 \(3\) 进行解答

3.4.2 最值

1. 最小值(点)与最大值(点)
   
   在定义域 \(I\) 有定义，\(x\in I\)，都有
   
   \(f(x)\geq f(x_0)\) 则 \(f(x_0)\) 是最小值，\(x_0\) 是最小值点
   
   \(f(x)\leq f(x_0)\) 则 \(f(x_0)\) 是最大值，\(x_0\) 是最大值点
   
   最值是一个全局概念，最值是唯一的

2. 求最值点
   
   找到定义域内所有：驻点，导数不存在的点，端点
   
   其中函数值最大的点为最大值点；函数值最小的点为最小值点

3. 特殊的最值点
   
   在 \(I\) 上连续且单调：最值点一定位于端点
   
   在 \(I\) 上有且只有一个极值点：该极值点一定是一个最值点

3.5 函数作图

1. 函数的水平渐近线
   
   若 \(\lim \limits_{x\to \infty}f(x)=a\)，则 \(y=a\) 是其的一条水平渐近线 (注意区分是朝正无穷渐进还是朝负无穷渐进)

2. 函数的垂直渐近线
   
   若 \(\lim \limits_{x\to x_0}f(x)=\infty\)，则 \(x=x_0\) 是其的一条垂直渐近线
   
   一般来说，分式函数 \(\frac{f(x)}{g(x)}\) 有垂直渐近线 \(x=x_0\)，则有 \(g(x_0)=0\)

3. 函数的斜渐近线
   
   函数在 \(x\) 趋于无穷时 \(y\) 趋于某条直线 \(y=kx+b\)，即 \(\lim \limits_{x\to \infty}f(x)=kx+b\)，即 \(y=kx+b\) 是其的一条斜渐近线
   
   对于 \(f(x)\) 的斜渐近线 \(y=kx+b\) 有
   
   \(\lim \limits_{x\to \infty}(f(x)-kx)=b\)
   
   \(\lim \limits_{x\to \infty} \frac{f(x)}{x}=\lim \limits_{x\to \infty}\frac{kx+b}{x}=\lim \limits_{x\to \infty}(k+\frac{b}{x})=k\)
   
   由上式可以看出，一般趋近无穷时表现为一次的函数才具有斜渐近线 (例分母的次数为分子的次数多 \(1\))

4. 例：求渐近线的相关题目
   
   求函数 \(f(x)=\frac{x^3}{x^2+2x-3}\) 的渐近线
   
   （1）\(\lim \limits_{x\to infty}f(x)=\infty\) 所以无水平渐近线
   
   （2）\(x^2+2x-3=0\) \(\therefore x=-3\) 或 \(1\) 所以有两条垂直渐近线 \(x=-3\) 与 \(x=1\)
   
   （3） \(\lim \limits_{x\to \infty}\frac{f(x)}{x}=\lim \limits_{x\to \infty}\frac{x^2}{x^2+2x-3}=1\)，\(\lim \limits_{x\to \infty}(f(x)-x)=-2\)，所以有一条斜渐近线 \(y=x-2\)

5. 微分法作图
   
   （1）找到定义域上：不连续点(一般是分母等于 \(0\) 的点)，与坐标轴相交的点
   
   （2）研究函数的奇偶性，周期性
   
   （3）研究函数的渐近线 (水平，垂直，斜)
   
   （4）研究 \(f'(x)=0, f''(x)=0\)，\(f', f''\) 不存在的点，以确定函数的极值点，驻点(增减性)，拐点(凹凸性)，并作出 \(f'-f''-f\) 表格
   
   （5）其他特殊点

4.1 不定积分

1. 定义与符号
   
   在微积分中，一个函数 \(f\) 的不定积分，或原函数，是一个导数等于 \(f\) 的函数 \(F\)，即 \(F'=f\)
   
   不定积分符号 \(\int\)：\(\int f(x)dx=F(x)+c\)
   
   若 \(F(x)\) 是 \(f(x)\) 的一个原函数，则我们将 \(f(x)\) 的全体原函数 \(F(x)+c\) 称为 \(f(x)\) 的不定积分

2. 一些性质

   • \([\int f(x)dx]'=f(x)\)
     
     \(\int f'(x)dx=f(x)+c\) (积分和求导可视为互为逆运算)
   • \(\int kf(x)dx=k\int f(x)dx\) (\(k\) 为常数或与 \(x\) 无关的变量)
   • \(\int [f_1(x)+f_2(x)+...+f_n(x)]dx=\int f_1(x)dx+\int f_2(x)dx+...+\int f_n(x)dx\) (\(n\)必须是有限的)

3. 基本积分公式

   • \(\int 0dx=c\)
   • \(\int kdx=kx+c\)
   • \(\int x^a dx=\frac{1}{a+1}x^{a+1}+c (a\neq -1)\)
   • \(\int \frac{1}{x}dx=\ln |x|+c\)
   • \(\int e^x dx=e^x+c\)
   • \(\int \sin x dx=-\cos x + c\)
   • \(\int \cos x dx=\sin x + c\)
   • \(\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x+c\)
   • \(\int \frac{1}{1+x^2}dx=\arctan x + c\)
   • \(\int a^xdx=\frac{1}{\ln a}a^x+c\)

4.2.1 第一换元积分法 (凑微分法)

1. 在求不定积分时，把被积分式凑成某个函数的微分的方法称为凑微分法：
   
   其核心是利用公式 \(dy=f'(x)dx\) 将微分 \(d\) 外面的某项 “拿” 到 \(d\) 里面去 (变成原函数) 并凑基本积分公式
   
   \(\int g(x)dx=\int f(\phi(x)) \phi'(x)dx=\int f(\phi(x))d\phi(x)=\int f(u)du=F(u)+c=F(\phi(x))+c\)

2. 例题
   
   
   
   
   
   
   
   若被积分式的三角函数 (\(\sin x, \cos x\)) 是奇数次，就将其中某一项拿到 \(d\) 里去，再运用 \(sin^2 x+cos^2 x=1\) 转换成统一的三角函数
   
   若本来就是偶数次，则运用倍角公式，和差化积等等公式进行统一

4.2.2 第二换元积分法

1. 第二类换元法的基本形式是 \(f(x), x=g(t),f(x)=f(g(t))\)，是在被积函数的自变量 \(x\) 后面增加一级自变量 \(t\) 取代原来的自变量，求出积分之后再回代 \(x\)
   
   使用第二类换元法是要改变被积函数形式的，通常用来积分根式、三角函数
   
   \(\int f(x)dx=\int f(\phi(t))\phi '(t)dt, x=\phi(t)\)

2. 例题
   
   
   
   

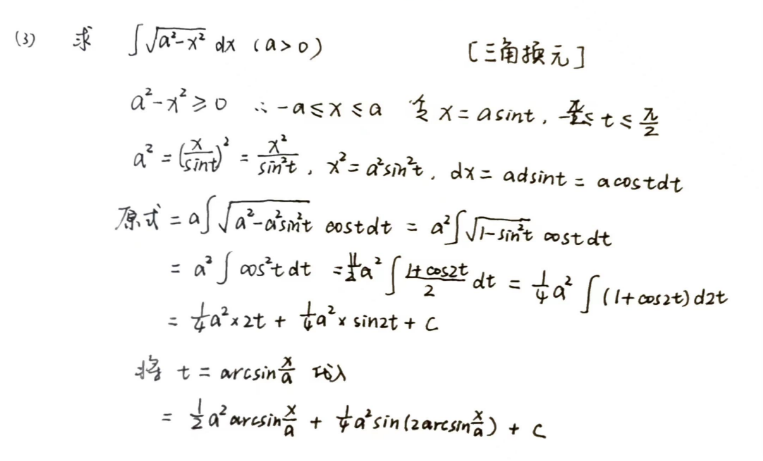
3. 一些常见三角换元题型总结的公式
   
   \(\int \frac{dx}{x^2-a^2}=\frac{1}{2a} \ln |\frac{x-a}{x+a}|+c\)
   
   \(\int \frac{dx}{a^2+x^2}=\frac{1}{2} \arctan \frac{x}{a}+c\)

4.2.3 分部积分法

1. 分部积分法推导
   
   对于求导公式 \(u'v'=u'v+v'u\) 等式两边同时对 \(x\) 求不定积分
   
   \(\int (u'v')dx=\int vu'dx+\int uv'dx\)
   
   \(\therefore uv=\int vdu+\int udv, \int udv=uv-\int vdu\)

2. 例题

   • \(\int x \sin x dx=-\int xd \cos x=-(x\cos x-\int \cos xdx)=-x\cos x+\sin x +c\)
   • \(\int xe^x dx=\int xde^x=xe^x-\int e^xdx=(x-1)e^x+c\)
   • \(\int x\ln xdx=\frac{1}{2} \int \ln x dx^2=\frac{1}{2}(x^2\ln x-\int x^2d\ln x)=\frac{1}{2}(x^2\ln x-\int xdx)=\frac{1}{2}(x^2\ln x-\frac{1}{2}x^2)+c\)
   • \(\int e^x\cos xdx=\int e^x d\sin x=e^x \sin x-\int \sin x de^x=e^x \sin x-\int e^x \sin xdx=e^x \sin x+ \int e^x d \cos x=e^x \sin x+e^x \cos x-\int \cos x de^x=e^x \sin x+e^x \cos x-\int e^x \cos x dx\)
     
     \(\therefore \int e^x\cos xdx=\frac{e^x \sin x+e^x \cos x}{2}+c\) （多次分部积分+方程思想）

3. 反(三角函数)对(数函数)幂(函数/多项式函数)指(数函数)三(角函数)，谁靠后谁与 \(d\) 结合再使用分部积分法

4.3 有理函数的积分

对形如 \(\frac{P(x)}{Q(x)}\) 的函数 (\(P(x), Q(x)\) 均为多项式) 求积分

1. 先将 \(\frac{P(x)}{Q(x)}\) 转化为真分式 (分母多项式的次数\(>\)分子多项式的次数)
   
   若 \(Q(x)\) 次数 \(< P(x)\) 次数：使用多项式除法(大除法) \(\frac{P(x)}{Q(x)}=a+\frac{P_1(x)}{Q(x)}\) ，此时得到真分式 \(\frac{P_1(x)}{Q(x)}\)
   
   若 \(Q(x)\) 次数 \(= P(x)\) 次数：使用配方法 \(\frac{P(x)}{Q(x)}=\frac{aQ(x)-aQ(x)+P(x)}{Q(x)}=a+\frac{P(x)-aQ(x)}{Q(x)}\) (\(a\) 取分子分母最高次项系数之比以消去分子的最高次项，以得到真分式)
   
   若 \(Q(x)\) 次数 \(> P(x)\) 次数：本身就是真分式，无需转化

2. 对于转化后形如 \(\int \frac{1}{ax^2+bx+c}dx\) 的真分式积分
   
   若 \(b^2-4ac=0\)：则 \(\int \frac{1}{ax^2+bx+c}dx=\int \frac{1}{a(x-x_1)^2}dx=\int \frac{1}{a}(x-x_1)^{-2}d(x-x_1)=-\frac{1}{a}(x-x_1)^{-1}+c\)
   
   若 \(b^2-4ac>0\)：则 \(\int \frac{1}{ax^2+bx+c}dx=\int \frac{1}{a(x-x_1)(x-x_2)}dx=\frac{1}{a} \int (\frac{A}{x-x_1}+\frac{B}{x-x_2})dx\)，这一步后使用待定系数法列方程解出 \(A\) 与 \(B\)，再分别求积分\(\int \frac{A}{x-x_1}d(x-x_1)+\int \frac{B}{x-x_2}d{x-x_2}=A\ln|(x-x_1)|+B\ln|(x-x_2)|+c\)
   
   若 \(b^2-4ac<0\)：则 \(ax^2+bx+c=a(x+x_1)^2+h=h(\sqrt{\frac{a}{h}}(x+x_1))^2+1\)，采用 \(\int \frac{1}{1+x^2}dx=\arctan x + c\) 公式求解

3. 对于转化后形如 \(\int \frac{dx+e}{ax^2+bx+c}dx\) 的真分式积分
   
   

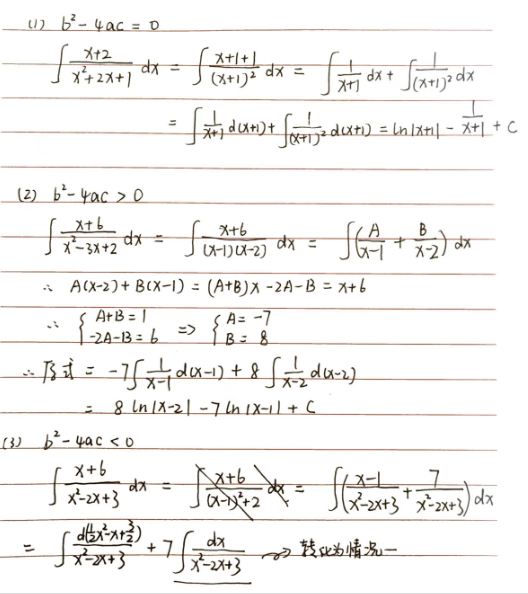
4. 其他