平衡树——splay 一

splay

一种平衡树，同时也是二叉排序树，与treap不同，它不需要维护堆的性质，它由Daniel Sleator和Robert Tarjan（没错，tarjan，又是他）创造，伸展树是一种自调整二叉树，它会将一个节点沿着到根的路径旋转上去。

空间效率：O_n

摊平时间效率：O_logn

建议先学会treap

treap（小根堆）模板 - yi_fan0305 - 博客园 (cnblogs.com)

treap（大根堆）模板 - yi_fan0305 - 博客园 (cnblogs.com)

---

存储结构

int ch[N][2],fa[N];//左孩子,右孩子,父亲
ll val[N],siz[N],cnt[N];//点值 

数组存储，也可以用结构体。

---

基本操作：

一、旋转

与treap的旋转无太大差异，只要注意更新父节点就行了，记得要更新siz。

splay的旋转函数的参数，是转上去的那个数值，这里与treap不同，treap是转下来的数值。

这里旋转一定要注意次序，明白先处理哪个，再处理哪个，否则会RE!

一定要先处理x与y的孩子，再处理x与y。

void pushup(int id)//更新siz
{
    siz[id]=siz[ch[id][0]]+siz[ch[id][1]]+cnt[id];
}
void spin(int x)
{
    rint y=fa[x],z=fa[y],d=(ch[y][1]==x);//d 判断x是y的左孩子还是右孩子
    ch[z][ch[z][1]==y]=x,fa[x]=z;//处理x与z的关系
    ch[y][d]=ch[x][d^1],fa[ch[x][d^1]]=y;//处理y的孩子与x的孩子的关系
    ch[x][d^1]=y;fa[y]=x;//处理y与x的关系
    pushup(y);//先更新y
    pushup(x);//在更新x
}

二、伸展

情况一：

x要移动到父节点的位置

自己懒得画了，用的教练课件上的图

直接旋转x即可

情况二：

情况二：X点要移到到g或更向上的位置且g->p和p->x是同一方向。

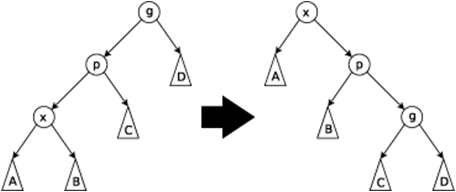
这里要先旋转p，再旋转x

情况三：

情况三：X点要移到到g或更向上的位置且g->p和p->x不是是同一方向。

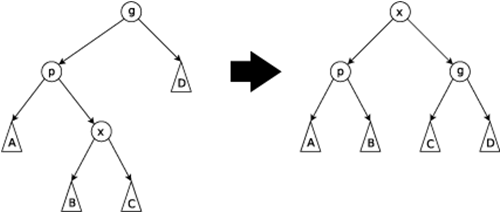
这里旋转两次x

你会发现，最后一次都是旋转x

void splay(int x,int goal)
{
    while(fa[x]!=goal)//判断是否已经到目标点的下边
    {
        rint y=fa[x],z=fa[y];
        if(z!=goal)//判断是情况一还是情况二、三
            (ch[y][0]==x)^(ch[z][0]==y)?spin(x):spin(y);
        //判断是情况二还是情况三
        spin(x);
    }
    if(goal==0)    root=x;//如果移动到了根节点,则更新根节点
}

三、插入节点

只要记得处理父节点就行了。

void insert(ll x)
{
    int u=root,fat=0;
    while(u&&val[u]!=x)//先向下找
    {
        fat=u;
        u=ch[u][x>val[u]];
    }
    if(u)    cnt[u]++;
    else
    {
        u=++tot;
        if(fat)    ch[fat][x>val[fat]]=u;//如果不是根节点,更新孩子节点
        fa[u]=fat;//插入操作
        val[u]=x;
        siz[u]=1;
        cnt[u]=1;
    }
    splay(u,0);//每次都要伸展,避免成链
}

四、查找结点

按照二叉排序树找到节点，然后将该节点伸展到到根节点就行了。

void find(ll x)
{
    int u=root;
    if(!u)    return;//不存在该节点,直接返回
    while(ch[u][x>val[u]]&&x!=val[u])//找到该节点的位置
        u=ch[u][x>val[u]];
    splay(u,0);//伸展
}

五、查找前驱后继

先将要查找的值的位置或相邻的位置伸展到根节点，然后在左右子树中搜索。

int get(ll x,int d)//d:0找前驱 1找后继
{
    find(x);//先伸展
    int u=root;
    if((val[u]>x&&d)||(val[u]<x&&!d))    return u;
    //如果该节点已经符合要求,直接返回位置
    u=ch[u][d];//找到左右子树
    while(ch[u][d^1])    u=ch[u][d^1];
    //找左子树中最大的或右子树中最小的(关键看你找前驱还是后继)
    return u;//返回前驱或后继的位置
}

六、删除节点

先找到前驱和后继，将前驱伸展到根节点，将后继伸展到前驱下面，根据二叉查找树的性质，后继的左孩子就是我们要删的点，进行操作即可。

void del(ll x)
{
    int pre=get(x,0),nxt=get(x,1);//找前驱后继
    splay(pre,0),splay(nxt,pre);//伸展
    int id=ch[nxt][0];//要删除的点
    if(cnt[id]>1)//如果这个数值有重复,直接--cnt即可
    {
        --cnt[id];
        splay(id,0);//伸展
    }
    else
    {
        ch[nxt][0]=0,fa[id]=0;//先切断联系
        val[id]=0,cnt[id]=0,siz[id]=0;//再进行删除
        pushup(nxt),pushup(pre);//最后更新siz
    }
}

---

最基础的就只有这些了，其他操作以后更新。

来自未来的链接：

平衡树——splay 二 - yi_fan0305 - 博客园 (cnblogs.com)

平衡树——splay 三 - yi_fan0305 - 博客园 (cnblogs.com)