一款 IDEA 插件帮你优雅转化 DTO、VO、BO、PO、DO

作者：小傅哥

博客：https://bugstack.cn

沉淀、分享、成长，让自己和他人都能有所收获！

一、承认你优秀很难

很多码农，把路走窄了

捧一个，喷一个，很多码农都不会多一点思路看问题，总是喜欢用矛和盾在显示自己有点本事。Github 你写文章说你不如做开源代码有价值，你写了开源代码说你这没有意义，那你问他贡献了啥，他只贡献了嘴。聊理论吹的叮当的，写代码搞的稀得囊的

好在，你这一路上能遇到很多同好，他们能真诚的给你意见、提供思路、帮助解决，让你们一群有技术初心的人，不断的成长。
这可能就是技术创作的土壤，如果大家都不施肥，反而还要过来用力的踩踩这块地，那最后大家都只能一起卷死在这，谁也不要创新。加油，我希望你可以和我一起做点事情

二、写了个什么插件

最近一个月多都在折腾关于 IDEA Plugin 插件开发的案例编写技术总结，在日常编码开发和折腾插件技术过程中发现一个痛点。

日常编码的过程中有太多的 vo2dto 对象转换操作，尤其是在 DDD 架构下多了不少的防腐层，而这层之间的对象 po、vo、do、dto，总是需要被转换，而使用 BeanUtils 多了，以后增改字段名都不知道影响到哪。

当然也有不错的工具 MapStruct 既可以保证性能又有不错的效率，但它需要给每一个转换对象维护对应的转换类，对于接口层的转换还是非常适合的，但那些很小的方法块内，也是如此折腾就显得有些麻烦了。

所以，小傅哥结合 IDEA Plugin 插件开发的能力，通过鼠标定位到转换对象上，一键织入需要生成一堆的 x.set(y.get) 方法，并且在几次优化中以及可以支持父类对象、lombok插件。演示图如下：

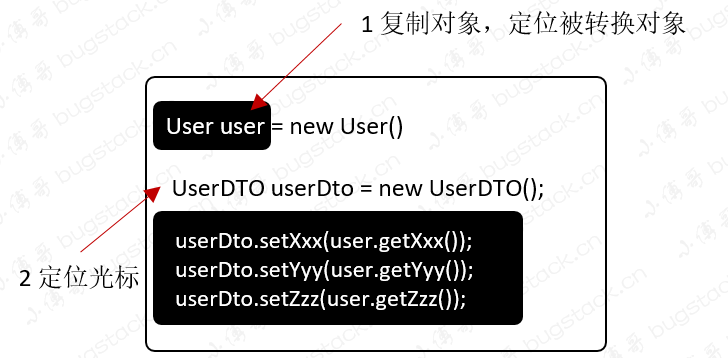
支持：复制一个对象，光标定位另外一个对象上，鼠标右键 Generate -> Vo2Dto 一键生成转换代码
支持：不复制对象，直接在转换可以生成空的 set 对象，方便自由添加内容
支持：插件中通过注解检测的方式，允许使用 lombok

三、发布插件的经历

原来不用英文描述，不给我过

1. 请用英语描述

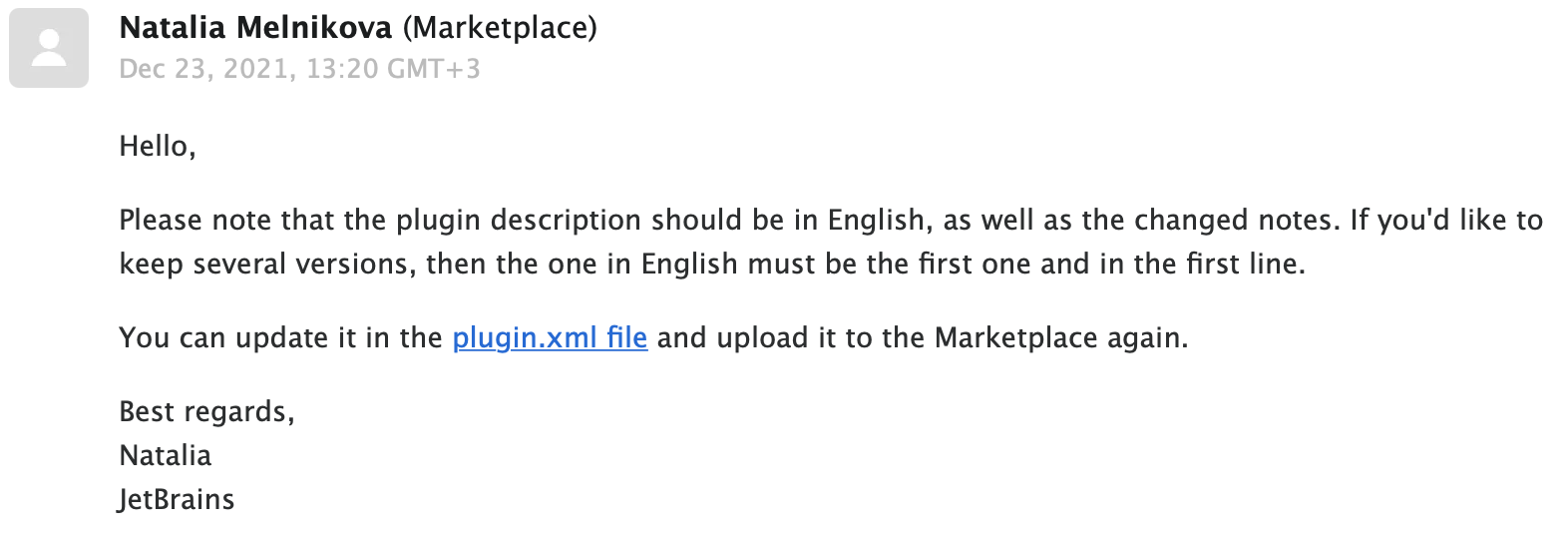
这是我第一次发布插件接收到的邮件提醒，告诉我在你的 plugin.xml 中，要用英语描述。一直没看，以为垃圾邮件

2. 请用英文截图

告诉我，你的截图要用英语的，这样我才能给你通过。

3. 说我截图没用

问我你确定需要这个截图吗，他觉得没啥意义

4. 终于发布出去

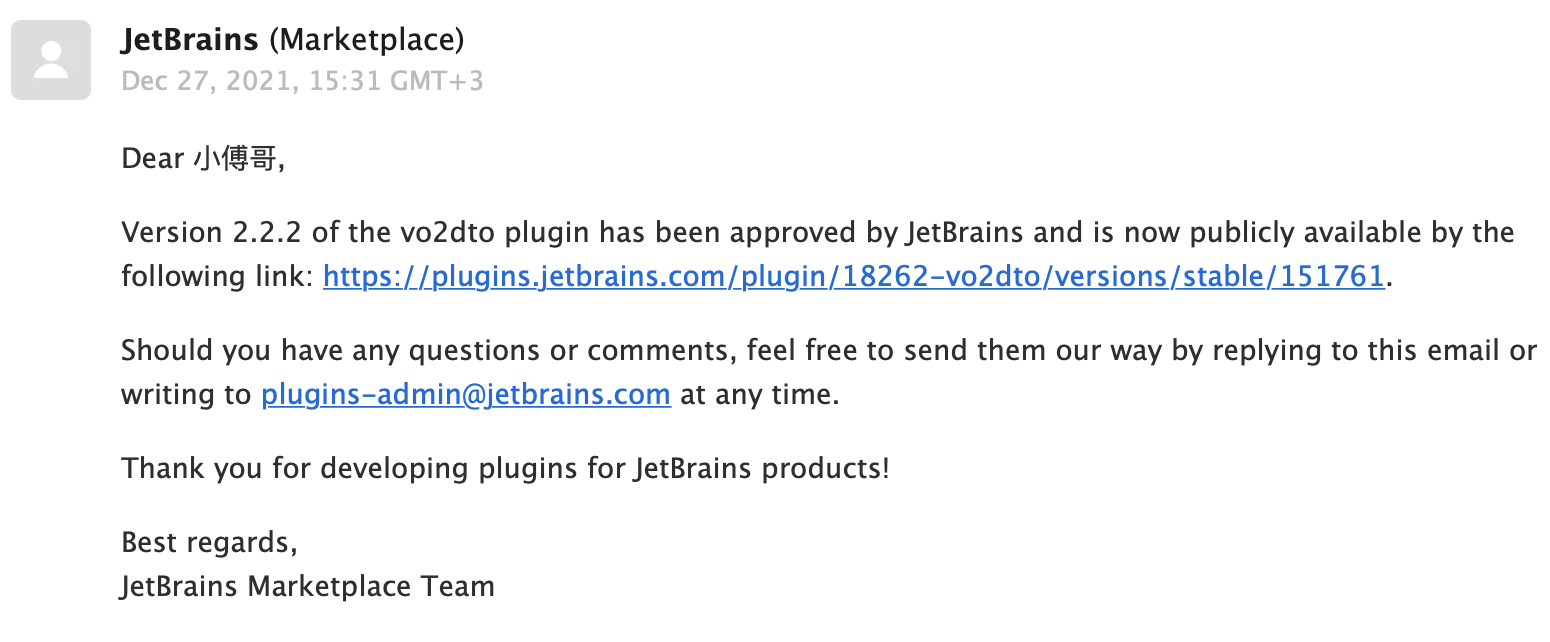
改了注释、删了截图，终于迎来曙光。你说，不发布一次，你会知道遇到这些吗！

四、把这插件安排上

1. 安装插件

讲到这我就兴奋了！

为啥兴奋，因为这一个插件发布，我整整等了2周，因为一次修改就要2个工作日才能审核，所以上面我犯的错，都是用时间磨出来。

不过现在好了，你可以直接在 IDEA 中搜索安装小傅哥写的插件了，哈哈哈，这种没做过的事搞一次，总是让人很兴奋！

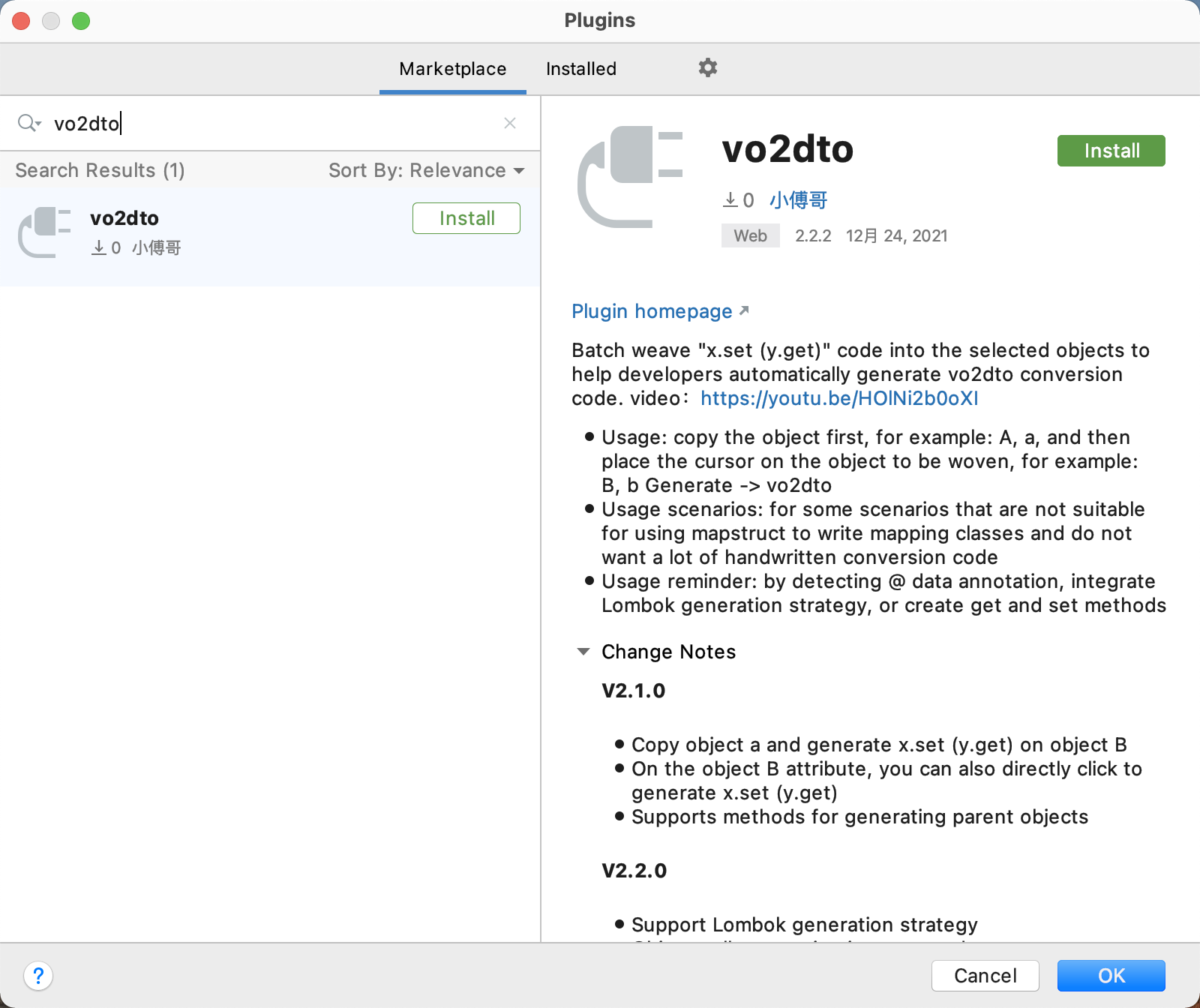
看到能搜索到 vo2dto 并顺利安装使用，我的心舒服了。没有人能阻挡你最技术的热爱，即使你来我这踩两脚

2. 使用介绍

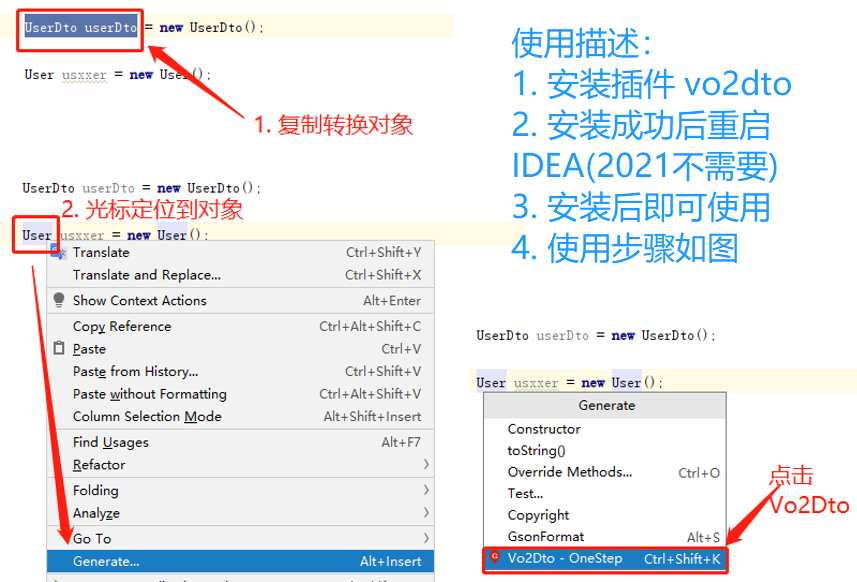
如图所示，你只需要很简单的步骤，既可以快速且准确的帮你生成对应的转换代码，在一些场景里使用还是非常 Good 的！操作步骤：

复制对象 UserDto userDto 这个是被转换对象，复制后才能便于生成获取属性的代码。如果你不复制，那么就是生成空代码
定位对象 User usxxer 把光标定位到对象或属性上，点击 Generate -> Vo2Dto 这样就可以把你的对象生成出来了。
注意：支持 lombok、支持继承对象，如果你在使用过程中遇到其他需求或者问题，都可以反馈给我

3. 源码共享

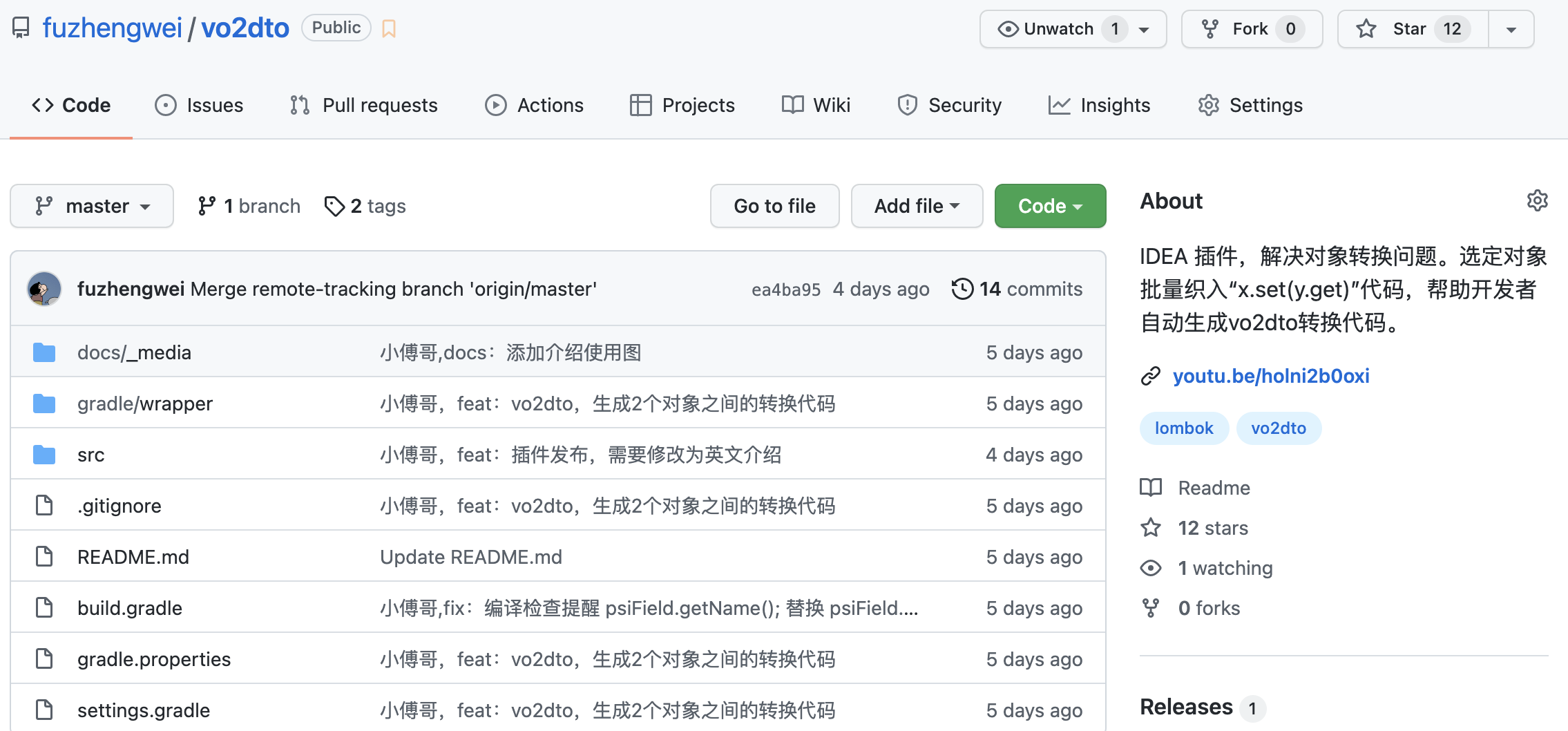
源码：https://github.com/fuzhengwei/vo2dto
说明：有同好的技术人共建才会让一件小事不断的优秀起来，所以我把这块代码共享出来，我们可以一起做一个非常短小精致的产品，来帮助我们自己完成一些便捷的开发处理。

五、我确定挺倔强

有一种倔强可能也是天生的，我喜欢技术、喜欢折腾、喜欢简单干净的事情，并把我认准的事长久坚持下去。有时候我也知道另外一条路会更轻松、更有钱拿，但那并不是我的内心，只有我认识到的我才是我，否则强加给我的我，始终不会是我。