NeurIPS 2022：基于语义聚合的对比式自监督学习方法

摘要：该论文将同一图像不同视角图像块内的语义一致的图像区域视为正样本对，语义不同的图像区域视为负样本对。

本文分享自华为云社区《[NeurIPS 2022]基于语义聚合的对比式自监督学习方法》，作者：Hint 。

1.研究背景

近些年来，利用大规模的强标注数据，深度神经网络在物体识别、物体检测和物体分割任务中取得巨大进展。然而，强标注数据耗时又耗力。为此，自监督学习方法提出从大量的无标注数据中学习出高效的特征编码器，然后利用该特征编码器在小规模数据上进行强监督训练，以此达到和在大规模强标注数据上训练的模型相当的性能。基于对比式自监督学习方法的出发点为：从不同视角来观察图像，将来自同一图像的不同视角的图像块视为正样本对，来自不同图像的图像块视为负样本对，通过拉近正样本对的特征的距离，拉远负样本对的特征的距离来监督特征编码器的学习。

然而，以上方法的基本假设（正样本对，即同一图像的不同视角的图像块，具有相同的语义）在以物体为中心的数据集（ImageNet）中成立，在以场景为中心的数据集（同一图像中包含多个物体，如COCO）中难以成立。为此，该论文将同一图像不同视角图像块内的语义一致的图像区域视为正样本对，语义不同的图像区域视为负样本对。

2.方法

本文方法和MoCo的框架类似，不同的是，本文将每类物体定义为一个可学习的类别向量S，根据类别向量S和图像特征图的每个位置计算相识度，聚合图像中同一类别的特征，然后将聚合后的类别特征构成正负样本对来进行对比训练学习。具体的网络结构如图1所示，其步骤包括：

同一图像经过数据增强得到不同的视角图像块，并分别输入图像编码器得到特征图；
将类别特征向量S和图像特征图计算每个位置的相似度，并根据相似度聚合得到图像中每个类别的特征；
得到两个视角下的聚合的类别特征后，拉近同类别特征间的距离，拉远不同类别特征之间的距离；
与此同时，拉近两个视角下，重叠图像区域的特征间的距离。

经过迭代训练后，图像特征编码器能够建模不同类别之间的语义特征，使得图像编码器更鲁棒。

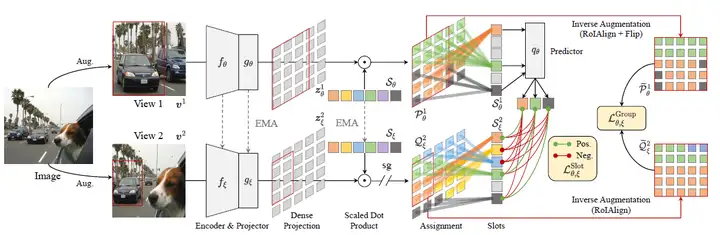
图1：SlotCon的流程图

3.实验结果：

主要实验结果如下表所示，可以看出，无论在目标检测还是分割任务上，该方法高出当前Image-level和Pixel-level的方法许多，证明了基于Object/Group-level的方法的优越性。另外，和Object/Group-level的方法相比，能够高出SOTA方法1.0%左右，表明了本文中可学习语义聚合方法的优势。

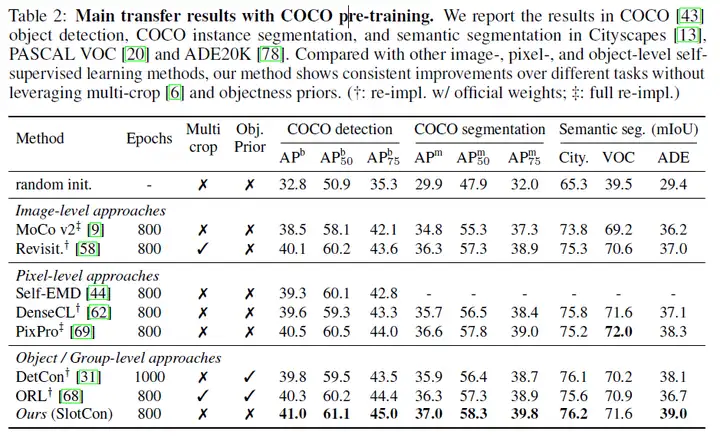
图2展示了无监督分割的定量和定性结果，该方法在此任务上取得不错性能。其mIoU值高出当前无监督分割方法3.92%。

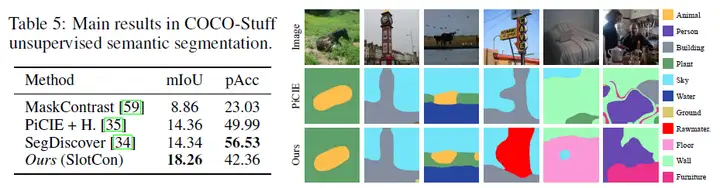
图2：无监督语义分割

图3展示了类别向量S和图像特征之间的相似度。可以看出，学习出的类别向量和图像中相应类别物体具有较高的相似度，说明图像特征编码器编码了较高的语义特征。

图3：类别特征向量S和图像特征间的相似度，红色区域为相似度较高区域

论文链接：[2205.15288] Self-Supervised Visual Representation Learning with Semantic Grouping (arxiv.org)

点击关注，第一时间了解华为云新鲜技术~