Python数据科学手册-机器学习: 支持向量机

support vector machine SVM

是非常强大、 灵活的有监督学习算法， 可以用于分类和回归。

贝叶斯分类器，对每个类进行了随机分布的假设，用生成的模型估计 新数据点 的标签。是属于 生成分类 方法。

判别分类：不再为每类数据建模，而是用一条分割线 或者 流形体 将各种类型分开。

原始数据：

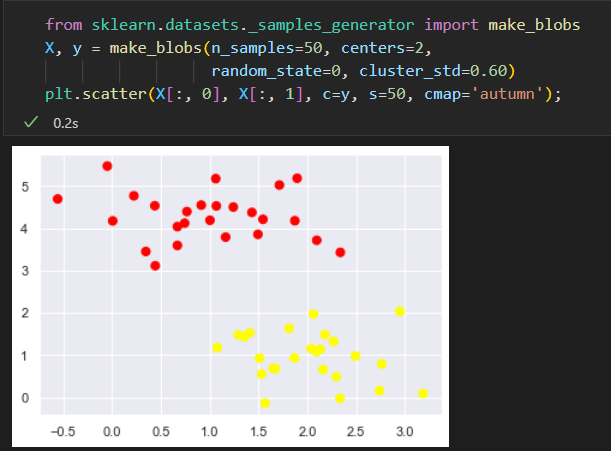
线性判别分类器 尝试 化一条 将数据 分成 俩部分的直线，这样就构成了一个分类模型。

可以发现不止一条直线可以将它们完美分割。

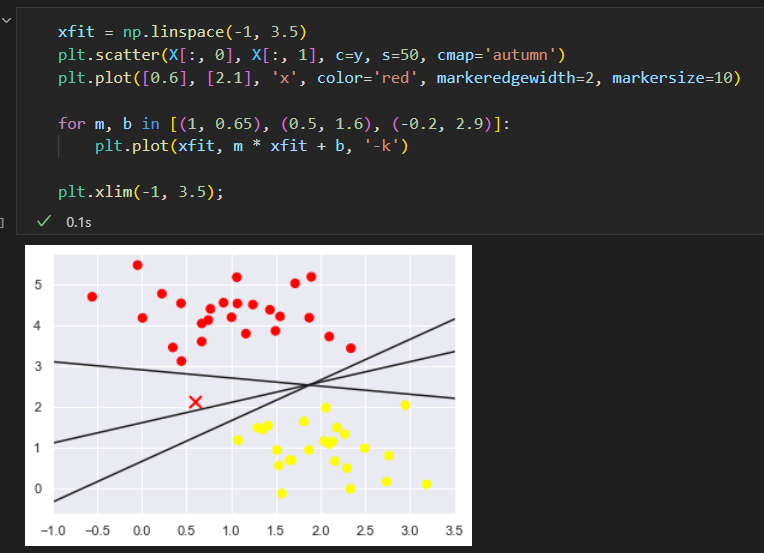
不同的分割线，会让新数据分配到不同的标签。

支持向量机：边界最大化

不是画一条细线来区分，而是画一条到最近点 边界 、有宽度 的线条。

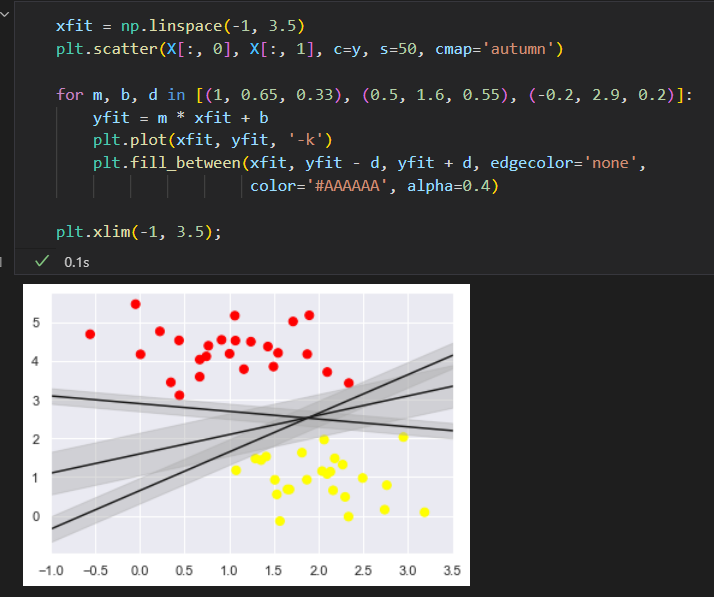
在支持向量机中，选择边界最大的那条线，是模型最优解。 边界最大化评估器。

拟合支持向量机

训练一个SVM模型，用一个线性核函数。并将参数C设置为一个很大的数。



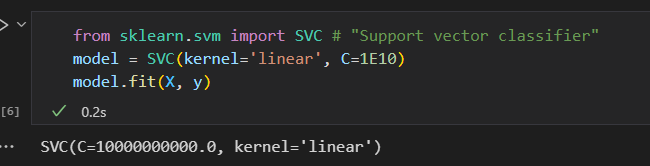
创建一个辅助函数画出SVM的决策边界。

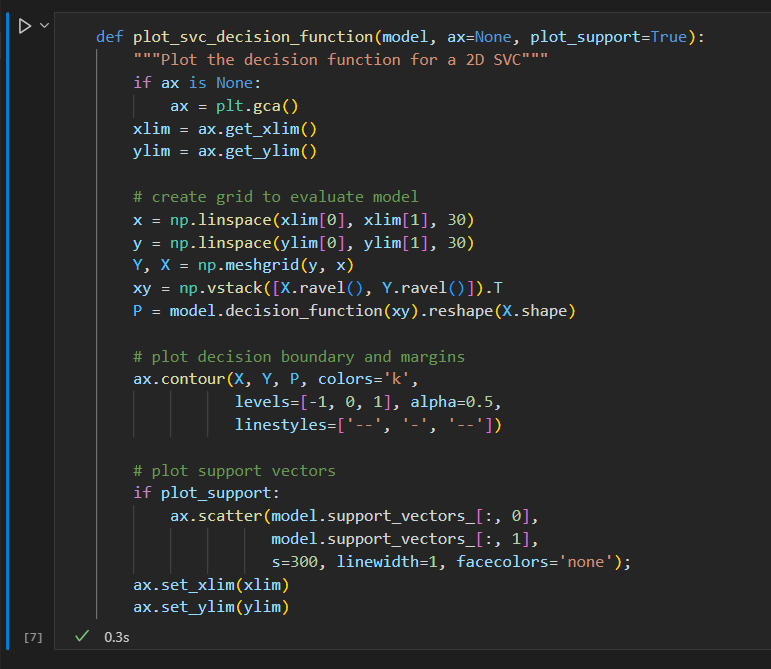
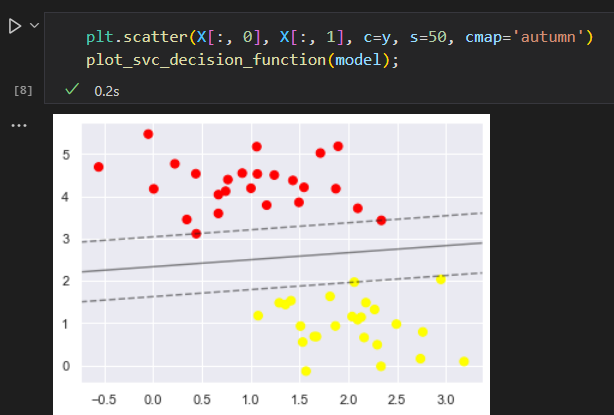
一些点正好在边界线上，这些点是拟合的关键支持点。被称为支持向量

支持向量的左边存放在分类器的support_vectors_ 属性中。

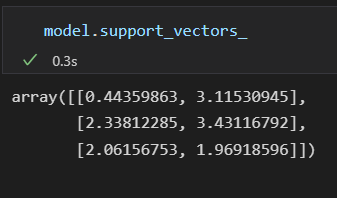
说明：任何在正确分类一侧远离边界线的点都不影响拟合结果。 因为这些点不会对拟合模型的损失函数产生任何影响，只要它们没跨越边界线，位置和数量就都无关紧要。

超越线性边界：核函数 SVM模型

将SVM模型 与 核函数 组合使用。功能会非常强大。

为了应用核函数，引入一些非线性可分数据。



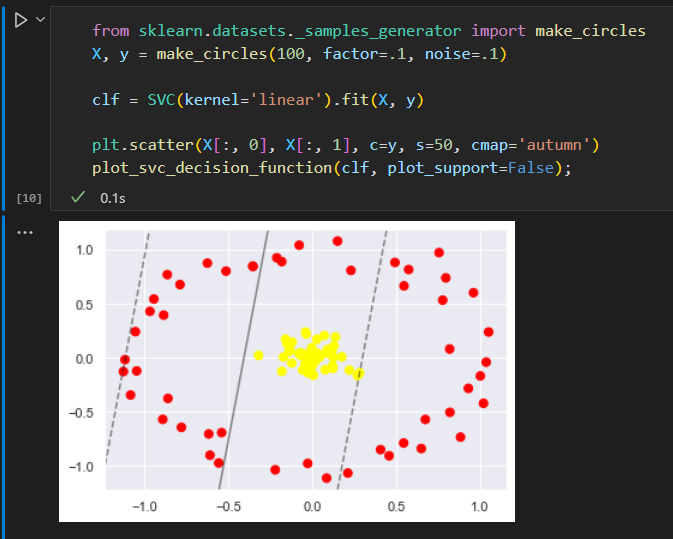
前面学到过，把数据投影到高维空间。从而使线性分割器派上用场。

一个简单的投影方法就是计算一个以 数据圆圈 为中心的径向基函数：



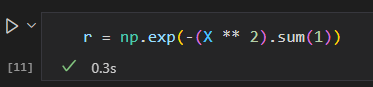
用三维图来可视化新增的维度

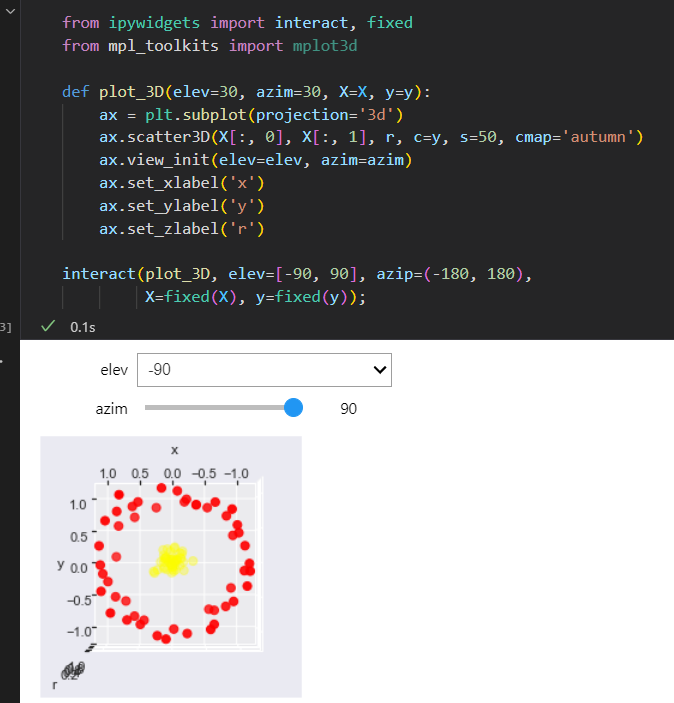
增加新的维度后，数据变成了线性可分状态，

通常选择基函数比较困难，我们需要让模型自动 指出 最合适的基函数。

一种 策略是计算基函数在数据集 上每个点的 变换结果，让SVM算法从所有结果中筛选出最优解。

这种基函数变换方式被称为 核变换

问题是：当N不断增大的时候，就会出现维度灾难。计算量巨大，

由于核函数技巧提供的小程序可以隐式计算 核变换数据的拟合。

在Scikit-Learn里面，我们可以应用核函数化的SVM模型，将线性核转变为 RBF (径向基函数)核。 设置kernel模型超参数即可。

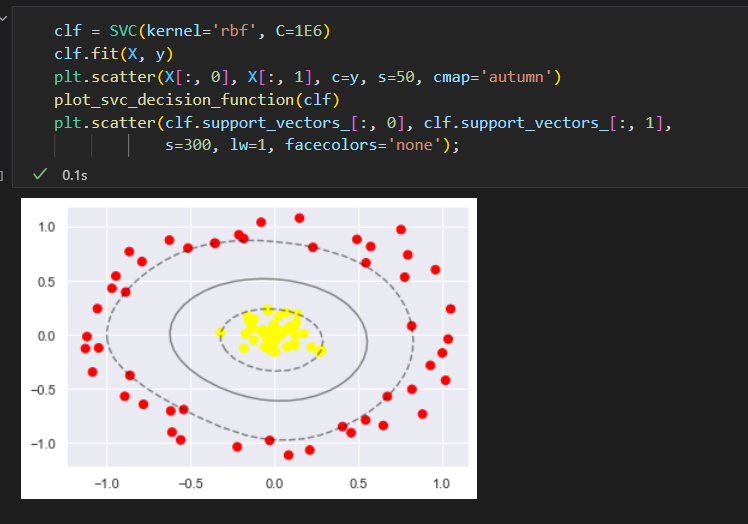
SVM优化：软化边界

如果数据有重叠，SVM实现了一些修正因子来“软化”边界，为了取得更好的拟合效果，允许一些点位于边界线之内。

边界线的硬度可以通过超参数进行控制，通常是C,

如果C很大，边界就会很硬，数据点便不能在边界内生存，

如果C比较小，边界就会较软，有一些数据点就可以穿越边界线。

案例：人脸识别

支持向量机总结

优点：

• 模型依赖的支持向量比较少，说明它们都是非常精致的模型，消耗内存少。
• 一旦模型训练完成，预测阶段速度非常快
• 由于模型只收边界线附近 的 点的影响，因此它们对于高维数据的学习效果非常好
• 与核函数方法的配合 极具通用性，能够适用不同类型的数据
  
  缺点：
• 随着样本量N的不断增加，最差的训练时间复杂度会达到O[N^3] .大样本学习的计算成本高
• 训练效果非常依赖于边界软化参数C的选择是否合理，这需要通过交叉检验自行搜索