洛谷 P2831 愤怒的小鸟

P2831 愤怒的小鸟

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0)(0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax^2+bxy=ax2+bx 的曲线，其中 a,ba,b 是Kiana 指定的参数，且必须满足 a < 0a<0，a,ba,b 都是实数。

当小鸟落回地面（即 xx 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 nn 只绿色的小猪，其中第 ii 只小猪所在的坐标为 \left(x_i,y_i \right)(xi​,yi​)。

如果某只小鸟的飞行轨迹经过了 \left( x_i, y_i \right)(xi​,yi​)，那么第 ii 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 \left( x_i, y_i \right)(xi​,yi​)，那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3)(1,3) 和 (3,3)(3,3)，Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4xy=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 TT 个关卡，现在 Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数 TT，表示游戏的关卡总数。

下面依次输入这 TT 个关卡的信息。每个关卡第一行包含两个非负整数 n,mn,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 nn 行中，第 ii 行包含两个正实数 x_i,y_ixi​,yi​，表示第 ii 只小猪坐标为 (x_i,y_i)(xi​,yi​)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0m=0，表示Kiana输入了一个没有任何作用的指令。

如果 m=1m=1，则这个关卡将会满足：至多用 \lceil n/3 + 1 \rceil⌈n/3+1⌉ 只小鸟即可消灭所有小猪。

如果 m=2m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 \lfloor n/3 \rfloor⌊n/3⌋ 只小猪。

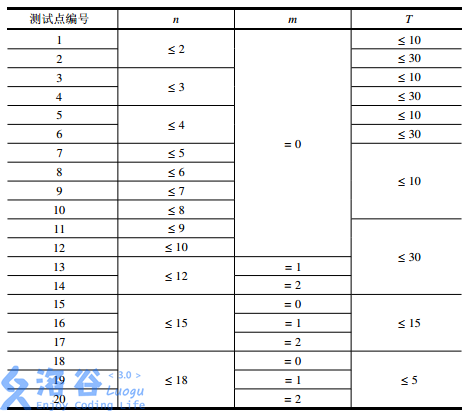
保证 1\leq n \leq 181≤n≤18，0\leq m \leq 20≤m≤2，0 < x_i,y_i < 100<xi​,yi​<10，输入中的实数均保留到小数点后两位。

上文中，符号 \lceil c \rceil⌈c⌉ 和 \lfloor c \rfloor⌊c⌋ 分别表示对 cc 向上取整和向下取整，例如：\lceil 2.1 \rceil = \lceil 2.9 \rceil = \lceil 3.0 \rceil = \lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例

输入样例#1： 复制

2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

输出样例#1： 复制

1
1

输入样例#2： 复制

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

输出样例#2： 复制

2
2
3

输入样例#3： 复制

1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99

输出样例#3： 复制

6

说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，22只小猪分别位于(1.00,3.00)(1.00,3.00)和 (3.00,3.00)(3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4xy=−x2+4x的小鸟即可消灭它们。

第二个关卡中有55只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6xy=−x2+6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
bool vis[];
double x[],y[];
int t,n,m,ans=0x7f7f7f7f;
struct nond{ double a,b; }p[];
double abss(double x){
    return x<?-x:x;
}
bool judge(int i,int j,int num){
    double a1=x[i]*x[i]*x[j],b1=x[j]*y[i];
    double a2=x[j]*x[j]*x[i],b2=x[i]*y[j];
    double ena=(b1-b2)/(a1-a2);
    double enb=(y[i]-x[i]*x[i]*ena)/x[i];
    if(ena>=-0.000000001)    return false;//直线弹道
    p[num].a=ena;p[num].b=enb;
    return true;
}
int work(int num){
    int cns=;
    for(int i=;i<=n;i++)
        if(!vis[i]){
            double eny=x[i]*x[i]*p[num].a+x[i]*p[num].b;
            if(abss(eny-y[i])<0.000000001){
                vis[i]=;
                cns++;
            }
        }
    return cns;
}
void dfs(int now,int tot){
    if(tot>=ans)    return ;
    if(now==n+){
        ans=tot;
        return ;
    }
    if(!vis[now]){
        bool f=;int bns[];
        for(int i=;i<=n;i++)    bns[i]=vis[i];
        for(int i=now+;i<=n;i++)
            if(!vis[i]&&judge(now,i,tot+)){
                f=;work(tot+);
                dfs(now+,tot+);
                for(int k=;k<=n;k++)    vis[k]=bns[k];
            }
        if(f==){    vis[now]=;dfs(now+,tot+);vis[now]=; }
    }
    else    dfs(now+,tot);
}
int main(){
    freopen("angrybirds.in","r",stdin);
    freopen("angrybirds.out","w",stdout);
    scanf("%d",&t);
    while(t--){
        memset(vis,,sizeof(vis));
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++)
            scanf("%lf%lf",&x[i],&y[i]);
        dfs(,);
        printf("%d\n",ans);
        ans=0x7f7f7f7f;
    }
    return ;
}

95暴力dfs